Euler’s Method

Euler’s Method
dy
dx
=
f
( x, y) , y( 0) = y0
y
Slope
=
=
Rise
Run
y
x
1
1
−
−
y
x
0
0
= f ( x 0 , y 0 )
( )( )
x 0
,y 0
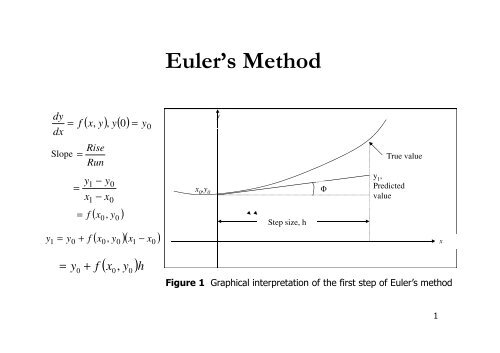
Step size, h
Φ
True value
y 1
,
Predicted
value
y
1 = y0
+ f x0, y0
x1
− x0
x
=
f ( x y )h
y0 +
0,
0
Figure 1 Graphical interpretation of the first step of Euler’s method
1

Euler’s Method
y
yi + 1
= yi
+ f ( xi,
yi
)h
True Value
h
= +1
x i
− x i
y i+1 , Predicted value
y i
Φ
h
Step size
x i x i+1
x
Figure 2 General graphical interpretation of Euler’s method
2

Euler’s Method
Write the first order differential equation in the form of
dy
dx
dy
dx
dy
dx
=
Example
−x
( 0) 5
+ 2 y = 1.3e
, y =
is rewritten as
−x
f
( x,
y)
yi + 1
= yi
+ f ( xi,
yi
)h
( 0) 5
= 1 .3e
− 2y,
y =
In this case
f
−x
( x, y) = 1.3e
− 2y
3

Example
A ball at 1200K is allowed to cool down in air at an ambient temperature
of 300K. Assuming heat is lost only due to radiation, the differential
equation for the temperature of the ball is given by
dθ
= −2.2067
× 10
dt
−12
4
8
( θ − 81×
10 ),
θ ( 0) = 1200 K
Find the temperature at t = 480
seconds using Euler’s method. Assume a step size of
h
= 240
seconds.
4

Solution
Step 1:
dθ
−12
4
8
= −2 .2067 × 10 ( θ − 81×
10 )
dt
−12
4
8
f ( t, θ) = −2.2067
× 10 ( θ − 81×
10 )
θi+
1
= θi
+ f ( ti,
θi
) h
θ1
= θ0
+ f ( t0,
θ0
) h
= 1200 + f ( 0,1200 ) 240
−12
4
8
= 1200 + ( − 2.2067 × 10 ( 1200 − 81×
10
) 240
= 1200 + ( − 4.5579)
240
= 106.09K
θ is the approximate temperature at t = t1 = t0
+ h = 0 + 240 = 240
1
θ 240 ≈ θ =106.09
1
( ) K
5

Solution Cont
Step 2:
For i = , t = 240, θ 106. 09
θ = θ + f
2
1
= 106.09
1
1 1
=
= 106.09 +
= 106.09 +
= 110.32K
( t1,
θ1)
h
+ f ( 240,106.09 )
−12
4
8
( − 2.2067 × 10 ( 106.09 − 81×
10
)
( 0.017595 )
240
240
240
θ is the approximate temperature at t = t2 = t1
+ h = 240 + 240 = 480
2
θ
( 480) ≈θ2 =110.32K
6

Solution Cont
The exact solution of the ordinary differential equation is given by the
solution of a non-linear equation as
θ −
0.92593ln
θ +
300
300
−1.8519 tan
−1
−3
( 0.00333θ
) = −0.22067×
10 t − 2. 9282
The solution to this nonlinear equation at t=480 seconds is
θ ( 480) =
647.57K
7

Comparison of Exact and Numerical
Solutions
1400
Temperature, θ(K)
1200
1000
800
600
400
200
0
Exact Solution
h=240
0 100 200 300 400 500
Time, t(sec)
Figure 3. Comparing exact and Euler’s method
8

Effect of step size
Table 1. Temperature at 480 seconds as a function of step size, h
Step, h θ(480) E t |є t |%
480
240
120
60
30
−987.81
110.32
546.77
614.97
632.77
1635.4
537.26
100.80
32.607
14.806
252.54
82.964
15.566
5.0352
2.2864
θ ( 480) =
647.57K
(exact)
9

Comparison with exact results
1500
θ(K)
Temperature,
1000
500
0
-500
-1000
Exact solution
h=120
h=240
0 100 200 300 400 500
Time, t (sec) h=480
-1500
Figure 4. Comparison of Euler’s method with exact solution for different step sizes
10

Effects of step size on Euler’s Method
800
Temperature,θ(K)
400
0
-400
-800
0 100 200 300 400 500
Step size, h (s)
-1200
Figure 5. Effect of step size in Euler’s method.
11

Errors in Euler’s Method
It can be seen that Euler’s method has large errors. This can be illustrated using
Taylor series.
2
3
dy
1 d y
2 1 d y
3
yi+ 1
= yi
+ ( xi+
1
− xi
) + ( x
1
− ) + (
1
− ) + ...
2 i+
xi
x
3 i+
xi
dx
2! dx
3! dx
y
x , y
i
i
x , y
i
i
1
1
1
= yi
+ f ( xi
, yi
)
i+
1 i
i i i+
1 i
i i i+
1
+
2!
3!
2
3
( x − x ) + f ' ( x , y )( x − x ) + f ' ' ( x , y )( x − x ) ...
i+ i
As you can see the first two terms of the Taylor series
x , y
i
i
yi + 1 = yi
+ f ( xi
, yi
)h
are the Euler’s method.
The true error in the approximation is given by
E
t
( x y ) f ′′( x , y )
f ′
i i 2 i i
= h + h
2!
3!
, 3
+ ...
12

13
Euler Method
)
Truncation Error
Global
)
Local Truncation Error
1,2,...
)
,
(
)
(
)
(
)
,
(
)
(
Euler Method
Problem
2
1
0
0
0
0
O(h
O(h
i
for
y
x
f
h
y
y
y
x
y
x
y
y
y
x
f
x
y
i
i
i
i
=
+
=
=
=
=
+
&

Introduction
Problem
y &(
x)
= f ( x,
y),
y(
x0)
=
to
be
The methods have the general
form:
yi +1
= yi
+
solved
h φ
is
For the case of Euler:
first order ODE :
φ =
( x , y i i
Different forms of φ will be used for
the Midpoint and Heun’s Methods.
a
y
0
f
)
14

15
Midpoint Method
)
Truncation Error
Global
)
Truncation Error
Local
)
,
(
)
,
(
2
)
(
)
(
)
,
(
)
(
Midpoint Method
Problem
2
3
2
1
2
1
1
2
1
0
0
0
0
O(h
O(h
y
x
f
h
y
y
y
x
f
h
y
y
y
x
y
x
y
y
y
x
f
x
y
i
i
i
i
i
i
i
i
+
+
+
+
+
=
+
=
=
=
=
&

Motivation
The midpoint can be summarized as:
Euler method is used to estimate the solution
at the midpoint.
The value of the rate function f(x,y) at the mid
point is calculated.
This value is used to estimate y i+1 .
Local Truncation error of order O(h 3 ).
Comparable to Second order Taylor series
method.
16

Midpoint Method
( x i
, yi
)
x
x
0 1
i+
1
i+
2
x
y
1
i+
2
=
y
i
+
h
f ( x
,
y
),
y
i i
i+
1 i
1 1
2 i+
i+
2 2
=
y
+
h
f ( x
,
y
)
17

Midpoint Method
slope =
f
( x i
, yi
)
( x i
, yi
)
x
x
0 1
i+
1
i+
2
x
y
1
i+
2
=
y
i
+
h
f ( x
,
y
),
y
i i
i+
1 i
1 1
2 i+
i+
2 2
=
y
+
h
f ( x
,
y
)
18

Midpoint Method
slope =
f
( x i
, yi
)
( x
,
y
1 1
i+ i+
2 2
)
( x i
, yi
)
x
x
0 1
i+
1
i+
2
x
y
1
i+
2
=
y
i
+
h
f ( x
,
y
),
y
i i
i+
1 i
1 1
2 i+
i+
2 2
=
y
+
h
f ( x
,
y
)
19

20
Midpoint Method
1
2
1
0 +
+
i
i
x
x
x
)
,
(
2
1
2
1
+
+
=
i
i
y
x
f
slope
)
,
( i
x i y
)
,
(
),
,
(
2 2
1
2
1
1
2
1
+
+
+
+
+
=
+
=
i
i
i
i
i
i
i
i
y
x
f
h
y
y
y
x
f
h
y
y
)
,
(
2
1
2
1
i+ i+
y
x

21
Midpoint Method
1
2
1
0 +
+
i
i
x
x
x
)
,
(
2
1
2
1
+
+
=
i
i
y
x
f
slope
)
,
( i
x i y
)
,
(
),
,
(
2 2
1
2
1
1
2
1
+
+
+
+
+
=
+
=
i
i
i
i
i
i
i
i
y
x
f
h
y
y
y
x
f
h
y
y
)
,
(
2
1
2
1
i+ i+
y
x

Example 1
Use the Midpoint Method to solve the ODE
y& ( x)
y(0)
= 1+
= 1
x
2
+ y
Use h = 0.1. Determine y(0.1) and y(0.2)
22

23
Example 1
1.4446
0.1(2.3438)
1.2103
)
,
(
1.3213
1.2103)
0.01
.05(1
1.2103
)
,
(
2
Step2 :
1.2103
1.1)
0.0025
0.1(1
1
)
,
(
1.1
1)
0
0.05(1
1
)
,
(
2
Step1:
0.1
1,
(0)
,
1
)
,
(
Problem :
2
1
1
2
1
1
1
2
1
1
1
2
1
1
2
1
0
2
1
0
0
1
0
0
0
2
1
0
0
2
=
+
=
+
=
=
+
+
+
=
+
=
=
+
+
+
=
+
=
=
+
+
+
=
+
=
=
=
=
+
+
=
+
+
+
+
+
+
y
x
f
h
y
y
y
x
f
h
y
y
y
x
f
h
y
y
y
x
f
h
y
y
h
y
y
y
x
y
x
f

Heun’s Predictor
Corrector
24

25
Heun’s Predictor Corrector Method
( )
)
Error
Truncation
Global
)
Error
Truncation
Local
)
,
(
)
,
(
2
:
Corrector
)
,
(
:
Predictor
)
(
)
(
)
,
(
)
(
Method
'
H
Problem
2
3
0
1
1
1
1
0
1
0
0
0
0
O(h
O(h
y
x
f
y
x
f
h
y
y
y
x
f
h
y
y
y
x
y
x
y
y
y
x
f
x
y
s
eun
i
i
i
i
i
i
i
i
i
i
+
+
+
+
+
+
=
+
=
=
=
=
&

Heun’s Predictor Corrector
(Prediction)
( x i
, y
0
+ 1 i+1
)
( x i
, yi
)
x i
x i+1
Prediction
0
y i + 1 = y i + h f ( x i , y i
)
26

Heun’s Predictor Corrector
(Prediction)
( x i
, y
0
+ 1 i+1
)
slope
= f ( x i
, yi
0
+1 +1
)
( x i
, yi
)
Prediction
x i
x i+1
0
y h f ( x , y
i+
1 i
i i
y = +
)
27

Heun’s Predictor Corrector
(Correction)
slope
f ( x
,
y
) + f ( x
2
0
=
i i
i+1 i+1
,
y
)
( x i
, y
0
+ 1 i+1
)
( x i
, yi
)
( x i
, y
1
+ 1 i+1
)
x i
x i+1
y
h
2
(
0
f ( x , y ) f ( x , y ))
1
i+ 1
= yi
+
i i
+
i+
1 i+
1
28

Example 2
Use the Heun's
Method to solve the ODE
y& ( x)
y(0)
= 1+
= 1
x
2
+ y
Use h = 0.1. One correction only
Determine y(0.1) and y(0.2)
29

30
Example 2
( )
( ) 4452
1.
)
,
(
)
,
(
2
Corrector :
1.4326
)
,
(
:
Predictor
Step 2 :
1.2105
)
,
(
)
,
(
2
Corrector :
1.2
0.1(2)
1
)
,
(
:
Predictor
Step1:
0.1
1,
)
(
,
1
)
,
(
Problem :
0
2
2
1
1
1
1
2
1
1
1
0
2
0
1
1
0
0
0
1
1
0
0
0
0
1
0
0
2
=
+
+
=
=
+
=
=
+
+
=
=
+
=
+
=
=
=
=
+
+
=
y
x
f
y
x
f
h
y
y
y
x
f
h
y
y
y
x
f
y
x
f
h
y
y
y
x
f
h
y
y
h
x
y
y
x
y
y
x
f

Summary
Euler, Midpoint and Heun’s methods are
similar in the following sense:
y = y + h ×
i +1 i
slope
Different methods use different estimates of
the slope.
Both Midpoint and Heun’s methods are
comparable in accuracy to the second
order Taylor series method.
31

32
Comparison
( )
)
,
(
)
(
)
(
)
,
(
2
Midpoint
)
,
(
)
,
(
2
Corrector :
)
(
)
(
)
,
(
:
Predictor
Method
Heun's
)
(
)
(
)
,
(
Euler Method
2
1
2
1
1
2
3
2
1
1
1
1
1
2
3
0
1
2
1
+
+
+
+
+
+
+
+
+
+
+
=
+
=
+
+
=
+
=
+
=
i
i
i
i
i
i
i
i
k
i
i
i
i
i
k
i
i
i
i
i
i
i
i
i
y
x
f
h
y
y
h
O
h
O
y
x
f
h
y
y
y
x
f
y
x
f
h
y
y
h
O
h
O
y
x
f
h
y
y
h
O
h
O
y
x
f
h
y
y
Method
Local
truncation
error
Global
truncation
error

Runge-Kutta Methods
33

Learning Objectives
To understand the motivation for using
Runge Kutta method and the basic idea
used in deriving them.
To Familiarize with Taylor series for
functions of two variables.
Use Runge Kutta of order 2 to solve
ODEs.
34

Motivation
We seek accurate methods to solve ODEs
that do not require calculating high order
derivatives.
The approach is to use a formula
involving unknown coefficients then
determine these coefficients to match as
many terms of the Taylor series
expansion.
35

Second Order Runge-Kutta Method
K
K
y
1
= h f
=
h
f
Problem :
Find α,
β ,
such that
( x
( x
,
i+
1
+ α h,
1
,
)
2
i
i+ 1 = yi
+ w1K
1 +
y
i
y
w
i
w
2
w
2
y
+
2
1
is as accurate as
i
K
β K
)
possible.
36

Taylor Series in Two
Variables
The Taylor Series is extended to the 2-
independent variable case.
This is used to prove RK formula.
37

Taylor Series in One Variable
The
f ( x
n
th
+ h)
=
order Taylor Series expansion of f(x)
i
n
i
n+
1
=∑
h ( i)
h ( n+
1)
f ( x)
+ f ( x)
i!
( n + 1)!
0
Approximation
Error
where x
is
between
x
and
x
+
h
38

Derivation of 2 nd Order
Runge-Kutta Methods – 1 of 5
Second Order Taylor Series
Used to solve ODE :
dy h
yi+
1 = yi
+ h +
dx 2
which is written as :
y
i+
1
=
y
i
+
h
f
( x
i
,
y
2
i
dy
dx
)
d
2
dx
+
=
y
2
2
h
2
f
f
Expansion
( x,
+ O(
h
'(
x
y)
i
3
,
)
y
i
)
+ O(
h
3
)
39

Derivation of 2 nd Order
Runge-Kutta Methods – 2 of 5
where
f
y
'(
x,
f
y)
'(
x,
=
∂f
Substituting
y)
:
( x,
∂x
is obtained by chain -
y)
+
∂f
( x,
∂y
( x,
2
⎛ ∂f
∂f
⎞ h
1
= yi
+ f ( xi,
yi
) h + ⎜ + f ( xi,
yi
) ⎟ O(
h
⎝ ∂x
∂y
⎠ 2
y)
dy
dx
rule differentiation
∂f
∂x
∂f
∂y
i +
+
=
+
f
y)
3
)
Eq. 1
f
'(
x,
y)
40

The Multivariable Chain Rule
41

42
Taylor Series in Two Variables
)
,
and (
)
,
joining between (
is on the line
)
,
(
)
,
(
1)!
(
1
)
,
(
!
1
...
2
2!
1
)
,
(
)
,
(
1
0
2
2
2
2
2
2
2
k
y
h
x
y
x
y
x
error
approximation
y
x
f
y
k
x
h
n
y
x
f
y
k
x
h
i
y
x
f
hk
y
f
k
x
f
h
y
f
k
x
f
h
y
x
f
k
y
h
x
f
n
n
i
i
+
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
∂
∂
+
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
∂
∂
=
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
+
∂
∂
+
∂
∂
⎟ +
⎠
⎞
⎜
⎝
⎛
∂
∂
+
∂
∂
+
=
+
+
+
=∑

Derivation of 2 nd Order
Runge-Kutta Methods – 3 of 5
Problem : Find α,
β ,
K
K
y
1
2
i+
1
= h f
= h f
=
y
i
( x
( x
+
i
i
,
)
+ α h,
w K
1
y
i
1
+
w
2
y
i
K
w
2
1
, w
2
+ β K
1
such that
)
Substituting :
y
i+
1
=
y
i
+
w h
1
f
( x
i
,
y
i
)
+
w h
2
f
( x
i
+ α h,
y
i
+
β K
1
)
43

Derivation of 2 nd Order
Runge-Kutta Methods – 4 of 5
44
...
)
,
(
)
,
(
)
(
...
)
,
(
)
(
...
)
,
(
)
,
(
:
...
)
,
(
)
,
(
2
2
2
2
2
1
1
1
2
2
1
1
1
2
1
1
1
1
+
∂
∂
+
∂
∂
+
+
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
∂
∂
+
∂
∂
+
+
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
∂
∂
+
∂
∂
+
+
+
=
+
∂
∂
+
∂
∂
+
=
+
+
+
+
+
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
y
x
f
y
f
h
w
x
f
h
w
y
x
f
h
w
w
y
y
y
f
K
x
f
h
w h
y
x
f
h
w
w
y
y
y
f
K
x
f
h
y
x
f
w h
y
x
f
w h
y
y
Substituting
y
f
K
x
f
h
y
x
f
K
y
h
x
f
β
α
β
α
β
α
β
α
β
α
Eq. 2

Derivation of 2 nd Order
Runge-Kutta Methods – 5 of 5
We derived two expansions for
y
i+
1
=
y
i
+ ( w
) h
⎛ ∂f
∂f
⎞ h 3
yi+
1 = yi
+ f ( xi,
yi
) h + ⎜ + f ( xi,
yi
) ⎟ + O(
h )
⎝ ∂x
∂y
⎠ 2
Matching terms, we obtain the following three equations :
1
1
w1
+ w2
= 1, w2α
= , and w2β
=
2
2
3 equations with 4 unknowns ⇒ infinite solutions
One possible solution :
1
+
w
2
f ( x ,
i
y
i
)
y
+
i+
1
α = β = 1,
2
:
w αh
w
2
1
∂f
∂x
=
w
+
2
2
w
=
2
βh
1
2
2
∂f
∂y
f ( x
i
,
y
i
)
+ ...
45

2 nd Order Runge-Kutta Methods
46
2
1
and
,
2
1
1,
:
such that
,
,
,
Choose
)
,
(
)
,
(
2
2
2
1
2
1
2
2
1
1
1
1
2
1
=
=
=
+
+
+
=
+
+
=
=
+
β
α
β
α
β
α
w
w
w
w
w
w
K
w
w K
y
y
K
y
h
x
f
h
K
y
x
f
h
K
i
i
i
i
i
i

47
Alternative Form
( )
2
2
1
1
1
1
2
1
)
,
(
)
,
(
Alternative Form
k
w
k
w
h
y
y
h k
y
h
x
f
k
y
x
f
k
i
i
i
i
i
i
+
+
=
+
+
=
=
+
β
α
2
2
1
1
1
1
2
1
)
,
(
)
,
(
Second Order Runge Kutta
K
w
w K
y
y
K
y
h
x
f
h
K
y
x
f
h
K
i
i
i
i
i
i
+
+
=
+
+
=
=
+
β
α

Choosing α, β, w 1 and w 2
For example, choosingα
= 1, then β = 1,
Second Order Runge -
K
K
1
2
=
=
h
h
f
f
( x
i
( x
1
yi
1 = yi
+ 1 2
2
This is Heun'
s Method
i
,
y
i
)
+ h,
y
i
+
K
Kutta method becomes :
1
)
h
i
2
i i
with a Single Corrector
( ) (
0
K + K = y + f ( x , y ) f ( x , y ))
+ +
w
1
=
w
2
i+
1
=
1
2
i+
1
48

Choosing α, β, w 1 and w 2
1 1
Choosingα
= then β = , w1
= 0, w2
= 1
2 2
Second Order Runge - Kutta method becomes :
K
K
y
1
2
i+
1
=
=
=
h
h
This is
y
i
f
f
( x
( x
+
i
i
,
K
2
y
+
)
h
2
the Midpoint
i
=
,
y
i
y
i
+
+
h
K
2
f
1
)
( x
i
+
Method
h
2
,
y
i
+
K
2
1
)
49

2 nd Order Runge-Kutta Methods
Alternative Formulas
α w
2
Pick
=
1
2
,
β w
2
=
1
2
any nonzeroα
number
,
w
1
+
w
2
= 1
: β = α,
w
2
=
1
,
2α
w
1
= 1−
1
2α
Second Order Runge Kutta Formulas (selectα
≠
K
K
y
1
2
i+
1
=
h
f ( x
,
y
i i
h f ( xi
+ α h,
yi
+
⎛ 1 ⎞
= yi
+ ⎜1
− ⎟K1
=
⎝
)
2α
⎠
+
α K
1
)
1
K
2α
2
0)
50

Second order Runge-Kutta Method
Example
Solve the following system to find
x&
( t)
= 1+
x
2
+
t
3
,
x(1)
= −4,
h
x(1.02)
using RK2
= 0.01, α = 1
STEP1:
K
K
1
2
= h
= h
f ( t
= 0.01(1 +
( x
x(1
+ 0.01) = x(1)
+
0
f ( t
0
= 1, x
0
= −4
+ (0.18 +
0
+ h,
x
0
+
= −4)
= 0.01(1 + x
+
K
0.18)
)
( K + K )
1
1
2
+ ( t
2
/ 2
+ .01)
0.1662) / 2 = −3.8269
0
2
0
3
+
t
3
0
) = 0.18
) = 0.1662
51

52
Second order Runge-Kutta Method
Example
( )
3.6662
0.1546)
(0.1668
2
1
3.8269
2
1
(1.01)
0.01)
(1.01
0.1546
)
.01)
(
0.1668)
(
0.01(1
)
,
(
0.1668
)
0.01(1
3.8269)
1.01,
(
STEP 2
2
1
3
1
2
1
1
1
1
2
3
1
2
1
1
1
1
= −
+
+
= −
+
+
=
+
=
+
+
+
+
=
+
+
=
=
+
+
=
= −
=
=
K
K
x
x
t
x
K
x
h
t
f
h
K
t
x
x
t
f
h
K

x& ( t)
=
1
+
x
2
( t)
+
t
3
,
x(1)
= −4,
Solution
for t
∈[1,2]
Using RK2,
α
=
1
CISE301_Topic8
L4&5
53

Applications of Runge-Kutta Methods
to Solve First Order ODEs
Using Runge-Kutta methods of different
orders to solve first order ODEs
54

2 nd Order Runge-Kutta RK2
Typical value of α = 1, Know as RK2
Equivalent to Heun' s method with a single corrector
k1
= f ( xi
, yi
)
k = f ( x + h,
y + k h)
y
2
i+
1
=
y
i
h
2
( k + k )
Local error is O(
h
i
+
1
i
3
2
1
) and global error is O(
h
2
)
55

Higher-Order Runge-Kutta
Higher order Runge-Kutta methods are available.
Derived similar to second-order Runge-Kutta.
Higher order methods are more accurate but
require more calculations.
56

57
3 rd Order Runge-Kutta RK3
( )
)
(
error is
and Global
)
(
error is
Local
4
6
)
2
,
(
)
2
1
,
2
(
)
,
(
RK3
Known as
3
4
3
2
1
1
2
1
3
1
2
1
h
O
h
O
k
k
k
h
y
y
h
k
h
k
y
h
x
f
k
h
k
y
h
x
f
k
y
x
f
k
i
i
i
i
i
i
i
i
+
+
+
=
+
−
+
=
+
+
=
=
+

58
4 th Order Runge-Kutta RK4
( )
)
(
error is
global
and
)
(
error is
Local
2
2
6
)
,
(
)
2
1
,
2
(
)
2
1
,
2
(
)
,
(
4
5
4
3
2
1
1
3
i
4
2
i
3
1
2
1
h
O
h
O
k
k
k
k
h
y
y
h
k
y
h
x
f
k
h
k
y
h
x
f
k
h
k
y
h
x
f
k
y
x
f
k
i
i
i
i
i
i
i
i
+
+
+
+
=
+
+
=
+
+
=
+
+
=
=
+

59
Higher-Order Runge-Kutta
( )
6
5
4
3
1
1
5
4
3
2
1
6
4
1
5
3
2
4
2
1
3
1
2
1
7
32
12
32
7
90
)
7
8
7
12
7
12
7
2
7
3
,
(
)
16
9
16
3
,
4
3
(
)
2
1
,
2
1
(
)
8
1
8
1
,
4
1
(
)
4
1
,
4
1
(
)
,
(
k
k
k
k
k
h
y
y
h
k
h
k
h
k
h
k
h
k
y
h
x
f
k
h
k
h
k
y
h
x
f
k
h
k
h
k
y
h
x
f
k
h
k
h
k
y
h
x
f
k
h
k
y
h
x
f
k
y
x
f
k
i
i
i
i
i
i
i
i
i
i
i
i
i
i
+
+
+
+
+
=
+
−
+
+
−
+
=
+
+
+
=
+
−
+
=
+
+
+
=
+
+
=
=
+

Example
4 th -Order Runge-Kutta Method
RK4
dy
= 1+
y +
dx
y(0)
= 0.5
x
2
h
=
0.2
Use
RK
4to compute
y(0.2)
and
y(0.4)
60

Example: RK4
Problem :
dy
2
= 1+
y + x ,
dx
Use RK 4 to find
y(0)
= 0.5
y(0.2),
y(0.4)
61

62
4 th Order Runge-Kutta RK4
( )
)
(
error is
global
and
)
(
error is
Local
2
2
6
)
,
(
)
2
1
,
2
(
)
2
1
,
2
(
)
,
(
4
5
4
3
2
1
1
3
i
4
2
i
3
1
2
1
h
O
h
O
k
k
k
k
h
y
y
h
k
y
h
x
f
k
h
k
y
h
x
f
k
h
k
y
h
x
f
k
y
x
f
k
i
i
i
i
i
i
i
i
+
+
+
+
=
+
+
=
+
+
=
+
+
=
=
+

63
Example: RK4
0.5
0,
1
)
,
(
0.2
0
0
2
=
=
+
+
=
=
y
x
x
y
y
x
f
h
( ) ( )
( ) ( )
( ) ( )
( ) 8293
0.
2
2
6
1.7908
0.2
0.16545
1
)
,
(
1.654
0.1
0.164
1
)
2
1
,
2
1
(
1.64
0.1
0.15
1
)
2
1
,
2
1
(
1.5
)
(1
)
,
(
4
3
2
1
0
1
2
0
0
3
0
0
4
2
0
0
2
0
0
3
2
0
0
1
0
0
2
2
0
0
0
0
1
=
+
+
+
+
=
=
+
+
+
+
=
+
+
=
=
+
+
+
+
=
+
+
=
=
+
+
+
+
=
+
+
=
=
+
+
=
=
k
k
k
k
h
y
y
x
y
h
k
y
h
x
f
k
x
y
h
k
y
h
x
f
k
x
y
h
k
y
h
x
f
k
x
y
y
x
f
k
(0.4)
(0.2),
4
0.5
(0)
,
1
Problem :
2
y
y
find
to
RK
Use
y
x
y
dx
dy
=
+
+
=
See RK4 Formula
Step 1

64
Example: RK4
0.8293
0.2,
1
)
,
(
0.2
1
1
2
=
=
+
+
=
=
y
x
x
y
y
x
f
h
( ) 2141
1.
2
2
6
0.2
2.0555
)
,
(
1.9311
)
2
1
,
2
1
(
1.9182
)
2
1
,
2
1
(
1.7893
)
,
(
4
3
2
1
1
2
3
1
1
4
2
1
1
3
1
1
1
2
1
1
1
=
+
+
+
+
=
=
+
+
=
=
+
+
=
=
+
+
=
=
=
k
k
k
k
y
y
h
k
y
h
x
f
k
h
k
y
h
x
f
k
h
k
y
h
x
f
k
y
x
f
k
(0.4)
(0.2),
4
0.5
(0)
,
1
Problem :
2
y
y
find
to
RK
Use
y
x
y
dx
dy
=
+
+
=
Step 2

Example: RK4
Problem :
dy
2
= 1+
y + x ,
dx
Use RK4
to find
y(0)
= 0.5
y(0.2),
y(0.4)
Summary of the solution
x i
y i
0.0 0.5
0.2 0.8293
0.4 1.2141
65

Summary
Runge Kutta methods generate an
accurate solution without the need to
calculate high order derivatives.
Second order RK have local truncation
error of order O(h 3 ) and global truncation
error of order O(h 2 ).
Higher order RK have better local and
global truncation errors.
N function evaluations are needed in the
N th order RK method.
66

Solving Systems of ODEs
67

Convert a single (or a system of) high
order ODE to a system of first order
ODEs.
Use the methods discussed earlier in this
topic to solve systems of first order
ODEs.
68

Outline
Solution of a system of first order ODEs.
Conversion of a high order ODE to a system of
first order ODEs.
Conversion of a system of high order ODEs to a
system of first order ODEs.
Use different methods to solve systems of first
order ODEs.
Use different methods to solve high order ODEs.
Use different methods to solve systems of high
order ODEs.
69

Solving a System of First Order ODEs
Methods discussed earlier such as Euler,
Runge-Kutta,… are used to solve first
order ordinary differential equations.
The same formulas will be used to solve
a system of first order ODEs.
In this case, the differential equation is a
vector equation and the dependent variable is
a vector variable.
70

Euler Method for Solving a System of
First Order ODEs
Recall Euler method for solving a first order ODE:
Given
dy(
x)
dx
=
f
( y,
x),
y(
a)
=
y
a
Euler Method :
y(
a
y(
a +
y(
a
+ h)
= y(
a)
+ h f ( y(
a),
a)
2h)
= y(
a
+ 3h)
= y(
a
+ h)
+ h f ( y(
a
+ 2h)
+ h f ( y(
a
+ h),
a + h)
+ 2h),
a + 2h)
71

Example - Euler Method
Euler method to solve a system of n first order ODEs.
Given
Euler
Y ( a
Y ( a
Y ( a
⎡ f1(
Y,
x)
⎤ ⎡ y1(
a)
⎤
⎢
( )
f2(
Y,
x)
⎥ ⎢
y2(
a)
⎥
d Y x
= F(
Y,
x)
= ⎢ ⎥,
Y ( a)
= ⎢ ⎥
dx
⎢ ... ⎥ ⎢ ... ⎥
⎢ ⎥ ⎢ ⎥
⎣ fn(
Y,
x)
⎦ ⎣yn(
a)
⎦
Method :
+ h)
= Y ( a)
+ h
+ 2h)
= Y ( a + h)
+
+ 3h)
= Y ( a
+ 2h)
+
F(
Y ( a),
a)
h F(
Y ( a
h F(
Y ( a
+ h),
a
+ h)
+ 2h),
a
+ 2h)
72

Solving a System of n First Order ODEs
Exactly the same
formula is used but
the scalar variables
and functions are
replaced by vector
variables and vector
value functions.
Y is a vector of
length n.
F(Y,x) is a vector
valued function.
⎡ y1(
x)
⎤
⎢
y2(
x)
⎥
Y ( x)
= ⎢ ⎥
⎢ ... ⎥
⎢ ⎥
⎣yn(
x)
⎦
⎡ d y
⎢
⎢
( )
d dx d Y x
y
=
⎢
dx ⎢ dx
⎢ ...
⎢d
y
⎢⎣
dx
Y ( a + h)
= Y ( a)
+ h
1
2
n
⎤
⎥ ⎡ f
⎥ ⎢
⎥ ⎢
f
=
⎥ ⎢
⎥ ⎢
⎥ ⎣ f
⎥⎦
( Y,
x)
⎤
( Y,
x)
⎥
⎥ =
... ⎥
⎥
( Y,
x)
⎦
F(
Y ( a),
a)
n×
1 vector
F(
Y,
x)
Y ( a + 2h)
= Y ( a + h)
+ h F(
Y ( a + h),
a + h)
1
2
n
Y
Y ( a + 3h)
= Y ( a + 2h)
+ h F(
Y ( a + 2h),
a + 2h)
is
73

74
Example :
Euler method for solving a system of first order ODEs.
⎥
⎦
⎤
⎢
⎣
⎡−
=
⎥
⎦
⎤
⎢
⎣
⎡
+
+
+
−
=
⎥
⎦
⎤
⎢
⎣
⎡
−
+
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
+
=
+
⎥
⎦
⎤
⎢
⎣
⎡−
=
⎥
⎦
⎤
⎢
⎣
⎡
+
+
+
−
=
⎥
⎦
⎤
⎢
⎣
⎡
−
+
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
+
=
+
=
⎥
⎦
⎤
⎢
⎣
⎡−
=
⎥
⎦
⎤
⎢
⎣
⎡
=
=
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⎥
⎦
⎤
⎢
⎣
⎡
1.39
0.78
0.9)
.1(1
1.2
0.12
0.9
(0.1)
1
(0.1)
0.1
(0.1)
(0.1)
(0.2)
(0.2)
)
),
(
(
)
(
)
2
(0
2 :
1.2
0.9
1)
0.1(1
1
0.1
1
(0)
1
(0)
0.1
(0)
(0)
(0.1)
(0.1)
(0),0)
(
(0)
)
(0
1:
0.1
1
1
(0)
(0)
(0)
),
,
(
1
)
(
)
(
1
2
2
1
2
1
1
2
2
1
2
1
2
1
1
2
2
1
y
y
y
y
y
y
h
h
Y
h F
h
Y
h
Y
STEP
y
y
y
y
y
y
Y
F
h
Y
h
Y
STEP
h
with
Method
Euler
of
steps
Two
y
y
Y
x
Y
F
y
y
x
y
x
y
&
&

75
Example :
RK2 method for solving a system of first order ODEs
⎥
⎦
⎤
⎢
⎣
⎡−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎥
⎦
⎤
⎢
⎣
⎡
+
⎥
⎦
⎤
⎢
⎣
⎡
+
⎥
⎦
⎤
⎢
⎣
⎡−
=
⎥
⎦
⎤
⎢
⎣
⎡
+
+
=
+
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
+
−
+
=
+
+
=
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
−
=
=
=
−
⎥
⎦
⎤
⎢
⎣
⎡−
=
⎥
⎦
⎤
⎢
⎣
⎡
=
=
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⎥
⎦
⎤
⎢
⎣
⎡
1.195
0.89
0.19
0.12
0.2
0.1
2
1
1
1
(0.1)
(0.1)
2)
1
0.5(
(0)
)
(0
0.19
0.12
0.1)
(0)
(
1
0.2
(0)
0.1
)
1,0
(0)
(
2
0.2
0.1
(0)
1
(0)
0.1
(0),0)
(
1
1:
0.1
Method
Kutta
second order Runge
1
1
(0)
(0)
(0)
),
,
(
1
)
(
)
(
2
1
1
2
1
2
2
1
1
2
2
1
y
y
K
K
Y
h
Y
y
y
h
K
Y
F
h
K
y
y
Y
F
h
K
STEP
h
with
of
steps
Two
y
y
Y
x
Y
F
y
y
x
y
x
y
&
&

76
Example :
RK2 method for solving a system of first order ODEs
⎥
⎦
⎤
⎢
⎣
⎡−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎥
⎦
⎤
⎢
⎣
⎡
⎥ +
⎦
⎤
⎢
⎣
⎡
⎥ +
⎦
⎤
⎢
⎣
⎡−
=
⎥
⎦
⎤
⎢
⎣
⎡
+
+
=
+
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
+
−
+
=
+
+
=
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
−
=
=
⎥
⎦
⎤
⎢
⎣
⎡−
=
⎥
⎦
⎤
⎢
⎣
⎡
=
=
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⎥
⎦
⎤
⎢
⎣
⎡
1.3780
0.7611
0.1771
0.1384
0.1890
0.1195
2
1
1.195
0.89
(0.2)
(0.2)
2)
1
0.5(
(0.1)
)
(0.1
0.1771
0.1384
0.1195)
(0.1)
(
1
0.189
(0.1)
0.1
)
1,0.1
(0.1)
(
2
0.1890
0.1195
(0.1)
1
(0.1)
0.1
(0.1),0.1)
(
1
2 :
1
1
(0)
(0)
(0)
),
,
(
1
)
(
)
(
2
1
1
2
1
2
2
1
1
2
2
1
y
y
K
K
Y
h
Y
y
y
h
K
Y
F
h
K
y
y
Y
F
h
K
STEP
y
y
Y
x
Y
F
y
y
x
y
x
y
&
&

Methods for Solving a System of First Order ODEs
We have extended Euler and RK2 methods to
solve systems of first order ODEs.
Other methods used to solve first order ODE can
be easily extended to solve systems of first
order ODEs.
77

High Order ODEs
How do solve a second order ODE?
&& x + 3 x&
+ 6x
=
1
How do solve high order ODEs?
78

The General Approach to Solve ODEs
High order ODE Convert System of first order ODEs Solve
&& x + 3x&
+ 6x
= 1
x&
(0) = 1; x(0)
=
4
Convert
⎡z&
⎢
⎣z&
1
2
⎤
⎥
⎦
Z(0)
⎡ z2
⎤
= ⎢ ⎥,
⎣1 − 3z2
− 6z1⎦
=
⎡4⎤
⎢ ⎥
⎣1⎦
Solve
Second order ODE
Two first order ODEs
CISE301_Topic8L6 79

Conversion Procedure
High order ODE Convert System of first order ODEs Solve
1. Select the dependent variables
One way is to take the original dependent
variable and its derivatives up to one degree less
than the highest order derivative.
2. Write the Differential Equations in terms of
the new variables. The equations come from the
way the new variables are defined or from the
original equation.
3. Express the equations in a matrix form.
80

Remarks on the Conversion Procedure
High order ODE Convert System of first order ODE Solve
1. Any n th order ODE is converted to a system of n
first order ODEs.
2. There are an infinite number of ways to select
the new variables. As a result, for each high
order ODE there are an infinite number of set of
equivalent first order systems of ODEs.
3. Use a table to make the conversion easier.
81

Example of Converting a High Order
ODE to First Order ODEs
Convert && x + 3x&
+ 6x
= 1, x&
(0) = 1; x(0)
= 4
to a system of first order ODEs
1.Select a
(Second order ODE
z
z
1
2
=
=
x
x&
new set of
variables
⇒
We need two variables)
One degree less than the
highest order derivative
82

Example of Converting a High Order
ODE to First Order ODEs
old new
name name
x
x&
z
z
1
2
Initial
cond.
4
1
Equation
z&
1
z&
2
=
z
2
= 1−
3z
2
−
6z
1
⎡ z&
⎢
⎣z&
1
2
⎤
⎥
⎦
=
⎡
⎢
⎣1
−
z
3z
2
2
−
6z
1
⎤
⎥,
⎦
Z(0)
=
⎡4⎤
⎢ ⎥
⎣1⎦
83

Example of Converting a High Order
ODE to First Order ODEs
Convert
&&& x + 2&&
x + 7x&
+ 8x
= 0
&& x(0)
= 9, x&
(0) = 1; x(0)
= 4
1.Select a
z
z
z
1
2
3
= x
= x&
= && x
new set of
variables (3 of
them)
One degree less than the
highest order derivative
84

85
Example of Converting a High Order
ODE to First Order ODEs
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
= −
=
=
9
1
4
(0)
,
8
7
2
8
7
2
9
1
4
cond.
name
name
Equation
Initial
new
old
1
2
3
3
2
3
2
1
1
2
3
3
3
3
2
2
2
1
1
Z
z
z
z
z
z
z
z
z
z
z
z
z
z
x
z
z
z
x
z
z
z
x
&
&
&
&
&&
&
&
&

Conversion Procedure for Systems of
High Order ODEs
System of high order ODEs Convert System of first order ODE Solve
1. Select the dependent variables
Take the original dependent variables and their
derivatives up to one degree less than the
highest order derivative for each variable.
2. Write the Differential Equations in terms of
the new variables. The equations come from the
way the new variables are defined or from the
original equation.
3. Express the equations in a matrix form.
86

Example of Converting a High Order
ODE to First Order ODEs
Convert
&&& x + 5&&
x +
&& y + 2xy
+ x&
= 2
x(0)
= 4; x&
(0) = 2; && x(0)
z
z
z
z
z
= x
= x&
= && x
= y
= y&
2x&
+ 8y
= 0
= 9; y(0)
= 1; y&
(0) = −3
1.Select a new set of variables ((3+
2) variables)
1
2
3
4
5
One degree less
than the highest
order derivative
87

Example of Converting a High Order
ODE to First Order ODEs
old new
name name
x
x&
&& x
y
y&
z
z
z
z
z
1
2
3
4
5
Initial
cond.
4
2
9
1
− 3
Equation
z&
z&
1
z&
z&
z&
2
3
4
5
=
=
z
z
2
2
3
= −5z
=
=
z
5
−
3
z
− 2z
2
2
− 2z
1
−8z
z
4
4
88

Solution of a Second Order ODE
Solve the equation using Euler method. Use h=0.1
&& x + 2x&
x(0)
=
+ 8x
= 1;
Select a
F(
Z)
=
=
x&
(0)
2
= −2
new set of
The second order equation is expressed as :
Z&
⎡z&
⎢
⎣z&
1
2
⎤
⎥
⎦
variables:
⎡ z
= ⎢
⎣2
− 2z
2
2
z
1
−8z
1
=
x,
z
2
⎤
⎥,
Z(0)
⎦
=
=
x&
⎡ 1 ⎤
⎢ ⎥
⎣−
2⎦
89

90
Solution of a Second Order ODE
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⎥
⎦
⎤
⎢
⎣
⎡
−
−
−
−
+
⎥
⎦
⎤
⎢
⎣
⎡
−
=
+
=
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⎥
⎦
⎤
⎢
⎣
⎡
−
−
−
−
+
⎥
⎦
⎤
⎢
⎣
⎡
−
=
+
=
+
=
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
2.2
0.58
8(0.8)
2.2)
2(
2
2.2
0.1
2.2
0.8
(0.1))
(
(0.1)
(0.2)
2.2
0.8
8(1)
2)
2(
2
2
0.1
2
1
(0))
(
(0)
0.1)
(0
0.1
,
2
1
(0)
,
8
2
2
)
(
1
2
2
Z
hF
Z
Z
Z
hF
Z
Z
h
Z
z
z
z
Z
F

Summary
Formulas used in solving a first order ODE
are used to solve systems of first order
ODEs.
Instead of scalar variables and functions, we
have vector variables and vector functions.
High order ODEs are converted to a set of
first order ODEs.
91