zadání

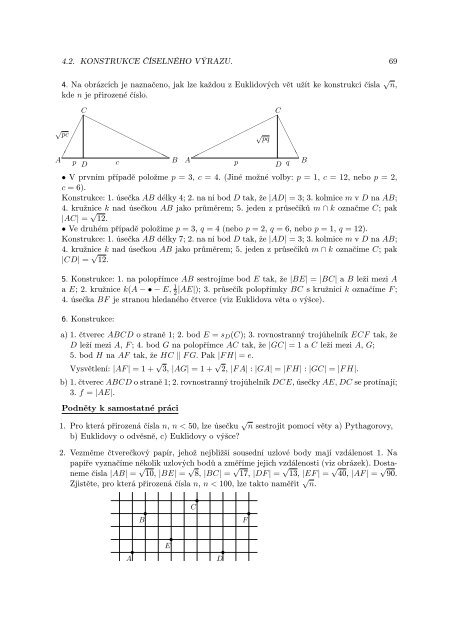
4.2. KONSTRUKCE ČÍSELNÉHO VÝRAZU. 694. Na obrázcích je naznačeno, jak lze každou z Euklidových vět užít ke konstrukci čísla √ n,kde n je přirozené číslo.CC❍ ✟✁ ❍❍❍❍❍❍❍❍❍❍✁✟✟ ❆√ ✟ ❆❆❆❆❆pc ✁✟✟ √✟ pq✁✟✁✟✟✁❍ ✟✟A pBD cA pBD q• V prvním případě položme p = 3, c = 4. (Jiné možné volby: p = 1, c = 12, nebo p = 2,c = 6).Konstrukce: 1. úsečka AB délky 4; 2. na ní bod D tak, že |AD| = 3; 3. kolmice m v D na AB;4. kružnice k nad úsečkou AB jako průměrem; 5. jeden z průsečíků m ∩ k označme C; pak|AC| = √ 12.• Ve druhém případě položíme p = 3, q = 4 (nebo p = 2, q = 6, nebo p = 1, q = 12).Konstrukce: 1. úsečka AB délky 7; 2. na ní bod D tak, že |AD| = 3; 3. kolmice m v D na AB;4. kružnice k nad úsečkou AB jako průměrem; 5. jeden z průsečíků m ∩ k označíme C; pak|CD| = √ 12.5. Konstrukce: 1. na polopřímce AB sestrojíme bod E tak, že |BE| = |BC| a B leží mezi Aa E; 2. kružnice k(A − • − E, 1 2|AE|); 3. průsečík polopřímky BC s kružnicí k označíme F ;4. úsečka BF je stranou hledaného čtverce (viz Euklidova věta o výšce).6. Konstrukce:a) 1. čtverec ABCD o straně 1; 2. bod E = s D (C); 3. rovnostranný trojúhelník ECF tak, žeD leží mezi A, F ; 4. bod G na polopřímce AC tak, že |GC| = 1 a C leží mezi A, G;5. bod H na AF tak, že HC ‖ F G. Pak |F H| = e.Vysvětlení: |AF | = 1 + √ 3, |AG| = 1 + √ 2, |F A| : |GA| = |F H| : |GC| = |F H|.b) 1. čtverec ABCD o straně 1; 2. rovnostranný trojúhelník DCE, úsečky AE, DC se protínají;3. f = |AE|.Podněty k samostatné práci1. Pro která přirozená čísla n, n < 50, lze úsečku √ n sestrojit pomocí věty a) Pythagorovy,b) Euklidovy o odvěsně, c) Euklidovy o výšce?2. Vezměme čtverečkový papír, jehož nejbližší sousední uzlové body mají vzdálenost 1. Napapíře vyznačíme několik uzlových bodů a změříme jejich vzdálenosti (viz obrázek). Dostanemečísla |AB| = √ 10, |BE| = √ 8, |BC| = √ 17, |DF | = √ 13, |EF | = √ 40, |AF | = √ 90.Zjistěte, pro která přirozená čísla n, n < 100, lze takto naměřit √ n.A • B • E • C • D • F •