Lekce - Realisticky cz
Lekce - Realisticky cz
Lekce - Realisticky cz
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
4.4.3 Další trigonometrické věty<br />
Předpoklady: 4402<br />
Věty, které objevíme v této hodině, mohou usnadnit některé výpočty, ale je možné se bez nich<br />
(na rozdíl od kosinové a sinové věty) obejít.<br />
Pedagogická poznámka: Následující dva příklady třída počítá najednou rozdělená do dvou<br />
skupin.<br />
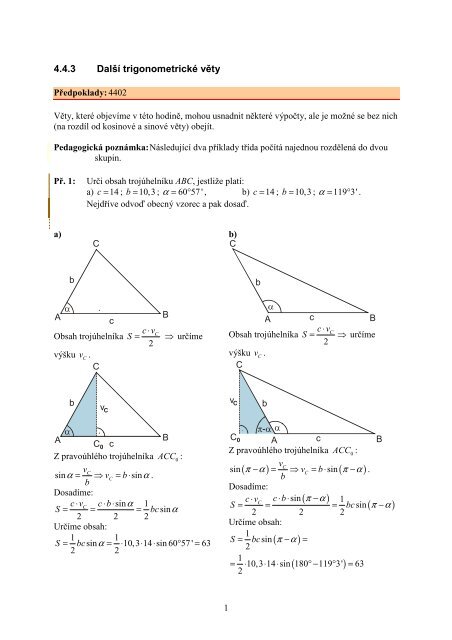
Př. 1:<br />
Urči obsah trojúhelníku ABC, jestliže platí:<br />
a) c = 14 ; b = 10,3 ; α = 60° 57 ' , b) c = 14 ; b = 10,3 ; α = 119° 3' .<br />
Nejdříve odvoď obecný vzorec a pak dosaď.<br />
a)<br />
C<br />
b)<br />
C<br />
b<br />
b<br />
A<br />
c<br />
Obsah trojúhelníka<br />
výšku v<br />
C<br />
.<br />
C<br />
B<br />
c ⋅v S = C<br />
⇒ určíme<br />
2<br />
A<br />
Obsah trojúhelníka<br />
výšku v<br />
C<br />
.<br />
C<br />
c<br />
B<br />
c ⋅v S = C<br />
⇒ určíme<br />
2<br />
b<br />
v C<br />
v C<br />
b<br />
A<br />
B<br />
C 0 c<br />
Z pravoúhlého trojúhelníka ACC<br />
0<br />
:<br />
vC<br />
sinα<br />
= ⇒ vC<br />
= b ⋅ sinα<br />
.<br />
b<br />
Dosadíme:<br />
c ⋅vC<br />
c ⋅b⋅sinα<br />
1<br />
S = = = bcsinα<br />
2 2 2<br />
Určíme obsah:<br />
1 1<br />
S = bcsinα<br />
= ⋅10,3⋅14 ⋅ sin 60° 57 ' = 63<br />
2 2<br />
C 0<br />
A c<br />
B<br />
Z pravoúhlého trojúhelníka ACC<br />
0<br />
:<br />
vC<br />
sin ( π − α ) = ⇒ vC<br />
= b ⋅sin<br />
( π − α ) .<br />
b<br />
Dosadíme:<br />
c ⋅v C<br />
c ⋅b⋅sin ( π −α<br />
) 1<br />
S = = = bc sin ( π − α )<br />
2 2 2<br />
Určíme obsah:<br />
1<br />
S = bcsin<br />
( π − α ) =<br />
2<br />
1<br />
= ⋅ 10,3 ⋅ 14 ⋅ sin ( 180 ° − 119 ° 3' ) = 63<br />
2<br />
1
Máme podobné vzorce a stejné výsledky ⇒ asi to není náhoda.<br />
60 57' 119 3' 180 sin 60° 57' = sin 180° − 119°<br />
3'<br />
° + ° = ° ⇒ ( )<br />
Navíc: ( ) ( )<br />
sin π − α = sinπ cosα − cosπ sinα = 0⋅cosα − − 1 sinα = sinα<br />
⇒<br />
1 1<br />
S = bcsin<br />
( π − α ) = bcsinα<br />
⇒ v obou případech jsme odvodili stejný vzorec<br />
2 2<br />
Vzorec platí pro všechny ostroúhlé i tupoúhlé trojúhelníky.<br />
Př. 2:<br />
Rozhodni, zda vzorec z předchozího příkladu platí i pro trojúhelník s pravým úhlem<br />
α .<br />
C<br />
b<br />
A<br />
c<br />
V pravoúhlém trojúhelníku platí vC<br />
B<br />
= b ⇒<br />
bc<br />
S = .<br />
2<br />
bc<br />
1 1 1<br />
Dosadíme: S = bcsinα<br />
= bcsin 90° = bc ⋅ 1 = .<br />
2 2 2 2<br />
Vztah platí i pro pravoúhlý trojúhelník.<br />
Tedy pro každý trojúhelník platí vzorec<br />
1<br />
S = bcsinα<br />
.<br />
2<br />
Př. 3:<br />
Přepiš vzorec pro výpočet obsahu i po další kombinace stran a úhlů.<br />
1<br />
Vzorec S = bcsinα<br />
umožňuje určit obsah trojúhelníku pomocí dvou stran a úhlu mezi nimi<br />
2<br />
1<br />
1<br />
⇒ další možnosti dvou stan a úhlu mezi nimi jsou S = ca sin β a S = absinγ<br />
.<br />
2<br />
2<br />
Pro každý trojúhelník ABC, jehož vnitřní úhly mají velikosti α , β , γ a strany délky a,<br />
1 1 1<br />
b, c platí : S = absin γ = bc sinα = casin<br />
β .<br />
2 2 2<br />
Př. 4: V trojúhelníku ABC je dáno: b = 6,7 ; β = 38°; γ = 73° . Urči jeho obsah.<br />
Pokud chceme použít předchozí vzorec pro obsah trojúhelníka, musíme určit dvě strany a úhel<br />
mezi nimi.<br />
Snadno můžeme dopočíst stranu c (sinová věta):<br />
b c sinγ<br />
sin 73°<br />
= ⇒ c = ⋅ b = ⋅ 6,7 = 10,4<br />
sin β sin γ sin β sin 38°<br />
Potřebujeme úhel mezi stranami b a c, tedy úhel α .<br />
2
( ) ( )<br />
α + β + γ = 180° ⇒ α = 180° − β + γ = 180° − 38° + 73° = 69°<br />
1 1<br />
Dosazení: S = bcsinα<br />
= ⋅6,7 ⋅10, 4⋅ sin 69° = 32,5<br />
2 2<br />
Obsah trojúhelníka ABC je 32,5.<br />
Př. 5:<br />
Je dán kvádr ABCDEFGH o délkách stran 2,3,4. Urči obsah trojúhelníku EBG.<br />
Nakreslíme si kvádr, na označení v tomto případě nezáleží (strany trojúhelníka jsou stěnové<br />
úhlopříčky všech druhů obdélníků, které se na kvádru vyskytují). Zvolíme například toto:<br />
AB = 3 ; BC = 2 ; AE = 4 .<br />
H<br />
G<br />
E<br />
F<br />
D<br />
C<br />
A<br />
B<br />
Pomocí Pythagorovy věty určíme délky jednotlivých stran trojúhelníku EBG.<br />
• Strana EB (přepona v pravoúhlém trojúhelníku ABE):<br />
2 2 2 2<br />
EB = AB + AE = 3 + 4 = 5 .<br />
• Strana BG (přepona v pravoúhlém trojúhelníku BCG):<br />
2 2 2 2<br />
BG = BC + CG = 2 + 4 = 2 5 .<br />
• Strana EG (přepona v pravoúhlém trojúhelníku EGH):<br />
2 2 2 2<br />
EG = GH + EH = 3 + 2 = 13 .<br />
Teď známe všechny strany v řešeném trojúhelníku:<br />
E<br />
G<br />
B<br />
Pokud chceme použít vzorec musíme vypočíst jeden z úhlů (například β ) pomocí kosinové<br />
( ) 2 2<br />
2 2 2 2<br />
5 + 2 5 − 13<br />
BE + BG − EG<br />
věty: cos β = = = 0,7155<br />
2⋅ BE ⋅ BG 2⋅5⋅<br />
2 5<br />
Dosadíme do vzorce pro výpočet obsahu:<br />
⇒ β = 44°<br />
19'<br />
3
1 1<br />
S = BE ⋅ BG ⋅ sin β = ⋅5⋅ 2 5 sin 44° 19' = 7,8<br />
2 2<br />
Obsah trojúhelníka BEG je 7,8.<br />
Př. 6: Najdi v tabulkách vzorec, který by umožnil spočítat obsah trojúhelníku BEG (z<br />
předchozího příkladu) přímo z délek jeho stran bez určování velikosti vnitřního úhlu.<br />
Pomocí nalezeného vzorce obsah vypočti a porovnej výsledky.<br />
Vzorec (Heronův) je v části se vzorci v kapitole o planimetrii a goniometrii na straně 35<br />
a + b + c<br />
v tomto znění: S = s ( s − a)( s − b)( s − c),<br />
s = .<br />
2<br />
a + b + c 5 + 2 5 + 13<br />
Určíme s: s = = ≐ 6,54<br />
2 2<br />
( )( )( ) ( )( )( )<br />
S = s s − a s − b s − c = 6,54 6,54 − 5 6,54 − 2 5 6,54 − 13 = 7,8<br />
Oba postupy vedou ke stejnému výsledku.<br />
Kromě vzorců pro obsah trojúhelníka existují i vzorce po výčet poloměru kružnice opsané a<br />
kružnice vepsané.<br />
Př. 7: V trojúhelníku ABC známe: AB = 12 a γ = 66° . Urči poloměr kružnice trojúhelníku<br />
opsané.<br />
Nakreslíme obrázek situace. Střed kružnice opsané leží na průsečíku os stran.<br />
C<br />
r<br />
S<br />
A<br />
S AB<br />
c<br />
B<br />
k<br />
Poloměr kružnic opsané spočteme z trojúhelníku ASS<br />
AB<br />
. Je pravoúhlý a platí: AS = r ;<br />
c<br />
AS<br />
AB<br />
= ; ∢ ASSAB<br />
= γ (je polovinou ∢ ASB , který je kvůli větě o obvodovém a středovém<br />
2<br />
úhlu dvojnásobkem úhlu γ ).<br />
c<br />
ASAB<br />
Platí sin<br />
2 c c<br />
γ = = = ⇒ r = .<br />
AS r 2r<br />
2sinγ<br />
Dosadíme:<br />
c 12<br />
r = = = 6,6<br />
2sinγ<br />
2⋅ sin 66°<br />
4
Dodatek: Je dobré si uvědomit, že trojúhelník ABC není v předchozím příkladě zcela<br />
zadaný. Známe jen dvě velikosti, vrchol C by mohl ležet kdekoliv na delším<br />
oblouku AB kružnice k. Trojúhelník by pak sice vypadal jinak, ale poloměr<br />
kružnice opsané by se nezměnil.<br />
Př. 8:<br />
Napiš další možné varianty vzorce odvozeného v předchozím příkladě.<br />
Poloměr kružnice opsané jsme počítali z úhlu a protější strany, platí tedy<br />
a b c<br />
r = = =<br />
2sinα 2sin β 2sin γ<br />
Př. 9:<br />
Najdi v tabulkách další vzorce pro výpočet poloměrů kružnice opsané a vepsané.<br />
Vzorce jsou v části se vzorci v kapitole o planimetrii a goniometrii na straně 35 v tomto znění:<br />
abc<br />
poloměr kružnice opsané : r = ,<br />
4S<br />
S a + b + c<br />
poloměr kružnice vepsané: ρ = , kde s = .<br />
s<br />
2<br />
abc<br />
Dodatek: Předchozí vzorce se někdy uvádějí ve tvarech: S = , S = ρs<br />
jako vzorce pro<br />
4r<br />
výpočet obsahu trojúhelníku.<br />
Př. 10: Urči obvod trojúhelníku, který je vepsán do kružnice o poloměru 7 cm, jestliže jeho<br />
vnitřní úhly mají velikosti: α = 67° ; β = 81° .<br />
Na první pohled neřešitelné. Hledáme nějaký vztah mezi poloměrem kružnice opsané a<br />
a<br />
velikostí strany ⇒ r = ⇒ a = r ⋅ 2sinα<br />
.<br />
2sinα<br />
Podobně můžeme vyjádřit i ostatní strany: b = r ⋅ 2sin β ; c = r ⋅ 2sin γ .<br />
o = a + b + c = r ⋅ 2sinα + r ⋅ 2sin β + r ⋅ 2sin γ = 2r<br />
( sinα + sin β + sin γ ) .<br />
Určíme úhel γ : α β γ γ ( α β ) ( )<br />
Dosadíme: o = r ( α + β + γ ) = ⋅ ( ° + ° + ° ) =<br />
+ + = 180° ⇒ = 180° − + = 180° − 67° + 81° = 32° .<br />
2 sin sin sin 2 7 sin 67 sin81 sin 32 34,1<br />
Trojúhelník má obvod 34,1 cm.<br />
Př. 11: Petáková:<br />
strana 50/cvičení 96<br />
strana 51/cvičení 100<br />
strana 51/cvičení 105<br />
Shrnutí:<br />
5