Gaussovy kvadratury Gaussian Quadrature
Gaussovy kvadratury Gaussian Quadrature Gaussovy kvadratury Gaussian Quadrature
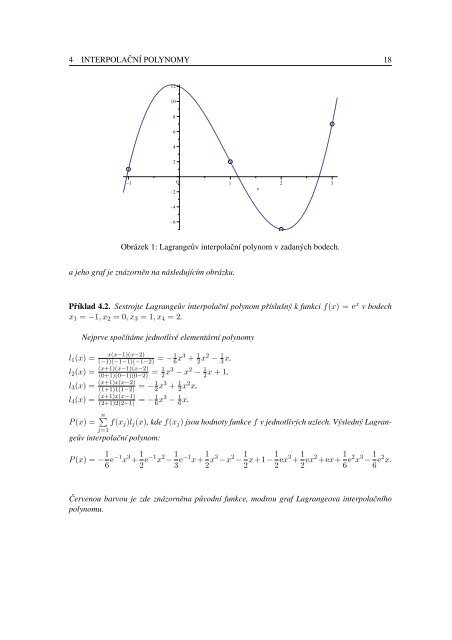
4 INTERPOLAČNÍ POLYNOMY 18 Obrázek 1: Lagrangeův interpolační polynom v zadaných bodech. a jeho graf je znázorněn na následujícím obrázku. Příklad 4.2. Sestrojte Lagrangeův interpolační polynom příslušný k funkci f(x) = e x v bodech x 1 = −1,x 2 = 0,x 3 = 1,x 4 = 2. Nejprve spočítáme jednotlivé elementární polynomy l 1 (x) = x(x−1)(x−2) (−1)(−1−1)(−1−2) = −1 6 x3 + 1 2 x2 − 1 3 x, l 2 (x) = (x+1)(x−1)(x−2) (0+1)(0−1)(0−2) = 1 2 x3 −x 2 − 1 2 x+1, l 3 (x) = (x+1)x(x−2) (1+1)1(1−2) = −1 2 x3 + 1 2 x2 x, l 4 (x) = (x+1)x(x−1) (2+1)2(2−1) = −1 6 x3 − 1 6 x. j=1 ∑ P(x) = n f(x j )l j (x), kdef(x j ) jsou hodnoty funkcef v jednotlivých uzlech. Výsledný Lagrangeův interpolační polynom: P(x) = − 1 6 e−1 x 3 + 1 2 e−1 x 2 − 1 3 e−1 x+ 1 2 x3 −x 2 − 1 2 x+1−1 2 ex3 + 1 2 ex2 +ex+ 1 6 e2 x 3 − 1 6 e2 x. Červenou barvou je zde znázorněna původní funkce, modrou graf Lagrangeova interpolačního polynomu.
4 INTERPOLAČNÍ POLYNOMY 19 Obrázek 2: Lagrangeův interpolační polynom příslušný k funkcif. 4.1.2 Chyba Lagrangeova interpolačního polynomu V případě, že se rozhodneme interpolovat funkci pomocí Lagrangeova interpolačního polynomu, dopouštíme se jisté chyby, kterou budeme značit R. Tato chyba bude rovněž funkcí a její hodnota se bude měnit v závislosti na proměnnéx. Pro určování odhadu chyby nám poslouží tento vztah R(x) = f(x)−P(x), x ∈ Df, kde f(x) je hodnota funkce f v bodě x a P(x) hodnota příslušného Lagrangeova interpolačního polynomu vypočítaného pomocí vztahu (7). Věta 4.2. Necht’ f je reálná funkce, která má v intervalu I vlastní n-tou derivaci (n ∈ N). Pak pro každé x ležící v intervaluI existuje bodξ z intervaluI takový, že platí R(x) = (x−x 1)(x−x 2 )...(x−x n ) f (n) (ξ), n! kdex 1 ,x 2 ,...,x n ∈ I, přičemžx 1 < x 2 < ··· < x n , jsou body, v nichž konstruujeme Lagrangeův polynom. Důkaz. Víme, že hodnoty polynomu v bodechx j odpovídají funkčním hodnotám funkcef, proto R(x j ) = 0 (∀j ∈ {1,2...,n}). (8) Zvolme tedy pevně x ∈ I, které je různé od x 1 ,x 2 ,...,x n , a definujme funkci F proměnnné t předpisem F(t) = (x−x 1 )(x−x 2 )...(x−x n )R(t)−(t−x 0 )(t−x 1 )...(t−x n )R(x).
- Page 1: VŠB - Technická univerzita Ostrav
- Page 5 and 6: Abstrakt Gaussova kvadratura je jed
- Page 7 and 8: OBSAH 7 11 Závěr 70 12 Literatura
- Page 9 and 10: 1 ÚVOD 9 1 Úvod Na základě pozn
- Page 11 and 12: 3 ORTOGONÁLNÍ SYSTÉMY POLYNOMŮ
- Page 13 and 14: 3 ORTOGONÁLNÍ SYSTÉMY POLYNOMŮ
- Page 15 and 16: 3 ORTOGONÁLNÍ SYSTÉMY POLYNOMŮ
- Page 17: 4 INTERPOLAČNÍ POLYNOMY 17 Polyno
- Page 21 and 22: 4 INTERPOLAČNÍ POLYNOMY 21 Přík
- Page 23 and 24: 4 INTERPOLAČNÍ POLYNOMY 23 4.2 He
- Page 25 and 26: 4 INTERPOLAČNÍ POLYNOMY 25 Podobn
- Page 27 and 28: 4 INTERPOLAČNÍ POLYNOMY 27 4.2.2
- Page 29 and 30: 4 INTERPOLAČNÍ POLYNOMY 29 Pro ab
- Page 31 and 32: 5 KVADRATURNÍ FORMULE A JEJÍ PŘE
- Page 33 and 34: 5 KVADRATURNÍ FORMULE A JEJÍ PŘE
- Page 35 and 36: 5 KVADRATURNÍ FORMULE A JEJÍ PŘE
- Page 37 and 38: 6 GAUSSOVA-LEGENDROVA KVADRATURNÍ
- Page 39 and 40: 6 GAUSSOVA-LEGENDROVA KVADRATURNÍ
- Page 41 and 42: 6 GAUSSOVA-LEGENDROVA KVADRATURNÍ
- Page 43 and 44: 6 GAUSSOVA-LEGENDROVA KVADRATURNÍ
- Page 45 and 46: 6 GAUSSOVA-LEGENDROVA KVADRATURNÍ
- Page 47 and 48: 6 GAUSSOVA-LEGENDROVA KVADRATURNÍ
- Page 49 and 50: 6 GAUSSOVA-LEGENDROVA KVADRATURNÍ
- Page 51 and 52: 6 GAUSSOVA-LEGENDROVA KVADRATURNÍ
- Page 53 and 54: 6 GAUSSOVA-LEGENDROVA KVADRATURNÍ
- Page 55 and 56: 6 GAUSSOVA-LEGENDROVA KVADRATURNÍ
- Page 57 and 58: 6 GAUSSOVA-LEGENDROVA KVADRATURNÍ
- Page 59 and 60: 7 GAUSSOVA-ČEBYŠEVOVA KVADRATURN
- Page 61 and 62: 8 GAUSSOVA-LAGUERROVA KVADRATURNÍ
- Page 63 and 64: 9 GAUSSOVA-HERMITOVA KVADRATURNÍ F
- Page 65 and 66: 9 GAUSSOVA-HERMITOVA KVADRATURNÍ F
- Page 67 and 68: 10 OBECNÁ GAUSSOVA KVADRATURA 67 P
4 INTERPOLAČNÍ POLYNOMY 18<br />
Obrázek 1: Lagrangeův interpolační polynom v zadaných bodech.<br />
a jeho graf je znázorněn na následujícím obrázku.<br />
Příklad 4.2. Sestrojte Lagrangeův interpolační polynom příslušný k funkci f(x) = e x v bodech<br />
x 1 = −1,x 2 = 0,x 3 = 1,x 4 = 2.<br />
Nejprve spočítáme jednotlivé elementární polynomy<br />
l 1 (x) =<br />
x(x−1)(x−2)<br />
(−1)(−1−1)(−1−2) = −1 6 x3 + 1 2 x2 − 1 3 x,<br />
l 2 (x) = (x+1)(x−1)(x−2)<br />
(0+1)(0−1)(0−2) = 1 2 x3 −x 2 − 1 2 x+1,<br />
l 3 (x) = (x+1)x(x−2)<br />
(1+1)1(1−2) = −1 2 x3 + 1 2 x2 x,<br />
l 4 (x) = (x+1)x(x−1)<br />
(2+1)2(2−1) = −1 6 x3 − 1 6 x.<br />
j=1<br />
∑<br />
P(x) = n f(x j )l j (x), kdef(x j ) jsou hodnoty funkcef v jednotlivých uzlech. Výsledný Lagrangeův<br />
interpolační polynom:<br />
P(x) = − 1 6 e−1 x 3 + 1 2 e−1 x 2 − 1 3 e−1 x+ 1 2 x3 −x 2 − 1 2 x+1−1 2 ex3 + 1 2 ex2 +ex+ 1 6 e2 x 3 − 1 6 e2 x.<br />
Červenou barvou je zde znázorněna původní funkce, modrou graf Lagrangeova interpolačního<br />
polynomu.