DeskriptivnÃ geometrie 1

Západočeská univerzita v Plzni 

Fakulta aplikovaných věd 

Katedra matematiky 

Deskriptivní geometrie 1 

Pomocný učební text 

1. část 

Světlana Tomiczková 

Plzeň – 2. října 2006– verze 2.0

Předmluva 

Tento pomocný text vznikl pro potřeby předmětu Deskriptivní geometrie I. Některé části jsou 

shodné s kapitolami ve skriptech pro strojní fakultu, které jsme vytvořili společně s doc. RNDr. 

Františkem Ježkem CSc. 

Chybí zde ještě pojednání o kuželosečkách, kótovaném promítání, řešení terénu a kartografických 

projekcích. Tyto chybějící kapitoly se objeví ve druhé části, která bude k dispozici v 

průběhu semestru. 

Pokud najdete v textu nedopatření, resp. pokud je text někde nesrozumitelný, prosím o sdělení 

takových poznatků. Ideální cestou je použití e-mailu a adresy svetlana@kma.zcu.cz. 

Autorka 

2

Obsah 

1 Opakování stereometrie 5 

1.1 Axiómy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 

1.2 Určování odchylek . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 

1.2.1 Odchylka mimoběžek . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 

1.2.2 Odchylka dvou rovin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 

1.3 Kritéria rovnoběžnosti . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 

1.4 Kritéria kolmosti . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 

1.5 Otáčení v prostoru . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 

1.6 Dělící poměr . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 

1.7 Kontrolní otázky . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 

2 Nevlastní elementy 10 

2.1 Úvodní úvaha . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 

2.2 Nevlastní bod, přímka a rovina . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 


3 Elementární plochy a tělesa 12 

3.1 Základní pojmy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 

3.1.1 Jehlanová plocha, jehlan . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 

3.1.2 Hranolová plocha, hranol . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 

3.1.3 Kuželová plocha, kužel . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 

3.1.4 Válcová plocha, válec . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 

3.1.5 Kulová plocha, koule . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 


4 Základy promítání 15 

4.1 Úvod . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 

4.2 Středové promítání . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 

4.3 Rovnoběžné promítání . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16 

4.4 Pravoúhlé promítání . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 

4.5 Středová kolineace . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 

4.6 Osová afinita . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21 

4.7 Kružnice v osové afinitě a středové kolineaci . . . . . . . . . . . . . . . . . . . . 23 


3

Obsah 4 

5 Mongeovo promítání 26 

5.1 Úvod . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26 

5.2 Obraz bodu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26 

5.3 Obraz přímky . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27 

5.4 Obraz roviny . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 

5.5 Polohové úlohy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 

5.5.1 Přímka v rovině (základní úloha Z1) . . . . . . . . . . . . . . . . . . . . 32 

5.5.2 Bod v rovině (základní úloha Z2) . . . . . . . . . . . . . . . . . . . . . . 35 

5.5.3 Rovnoběžné roviny (základní úloha Z3) . . . . . . . . . . . . . . . . . . . 37 

5.5.4 Průsečík přímky s rovinou (základní úloha Z4) . . . . . . . . . . . . . . . 38 

5.5.5 Průsečnice dvou rovin (základní úloha Z5) . . . . . . . . . . . . . . . . . 40 

5.6 Metrické úlohy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42 

5.6.1 Skutečná velikost úsečky (základní úloha Z6) . . . . . . . . . . . . . . . . 42 

5.6.2 Nanesení úsečky na přímku (základní úloha Z7) . . . . . . . . . . . . . . 44 

5.6.3 Přímka kolmá k rovině (základní úloha Z8) . . . . . . . . . . . . . . . . . 44 

5.6.4 Rovina kolmá k přímce (základní úloha Z9) . . . . . . . . . . . . . . . . 46 

5.6.5 Otočení roviny do polohy rovnoběžné s průmětnou (základní úloha Z10) . 47 

5.6.6 Obraz kružnice (základní úloha Z11) . . . . . . . . . . . . . . . . . . . . 50 

5.6.7 Transformace průměten (základní úloha Z12) . . . . . . . . . . . . . . . 51 


6 Axonometrie 53 

6.1 Úvod . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53 

6.2 Klasifikace axonometrií . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54 

6.3 Zobrazení bodu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55 

6.4 Zobrazení přímky . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56 

6.5 Zobrazení roviny . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57 

6.6 Úlohy v axonometrii . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58 

6.6.1 Vzájemná poloha přímek . . . . . . . . . . . . . . . . . . . . . . . . . . . 58 

6.6.2 Přímka v rovině . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59 

6.6.3 Průsečík přímky s rovinou . . . . . . . . . . . . . . . . . . . . . . . . . . 60 

6.6.4 Průsečnice rovin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61 

6.6.5 Kružnice v souřadnicové rovině . . . . . . . . . . . . . . . . . . . . . . . 62 

6.7 Pravoúhlá axonometrie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63 

6.7.1 Metrické úlohy v rovinách xy, yz, zx . . . . . . . . . . . . . . . . . . . . 64 

6.7.2 Obraz kružnice ležící v některé souřadnicové rovině . . . . . . . . . . . . 66 

6.8 Kontrolní otázky . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67

Kapitola 1 

Opakování stereometrie 

Na úvod připomeneme základní pojmy a věty z prostorové geometrie, které budeme používat 

v dalších kapitolách. 

1.1 Axiómy 

Axiómy jsou jednoduchá tvrzení, která nemůžeme dokázat. Z nich se potom odvozují další věty. 

Tento systém axiómů použil před více než 2000 lety slavný řecký geometr Euklides k vybudování 

prostorové geometrie. Geometrii vybudované na tomto systému axiómů říkáme Euklidovská 

geometrie. 

Uvedeme si pět základních axiómů prostorové geometrie: 

1. axióm: Dva různé body A, B určují právě jednu přímku p. Symbolicky tuto větu zapíšeme: 

∀A, B; A ≠ B ∃! p = AB. 

2. axióm: Přímka p a bod A, který neleží na přímce p, určují právě jednu rovinu α. Symbolicky: 

∀A, p; A /∈ p ∃! α = (A, p). 

3. axióm: Leží-li bod A na přímce p a přímka p v rovině α, leží i bod A v rovině α. Symbolicky: 

∀A, p, α; A ∈ p ∧ p ⊂ α ⇒ A ∈ α. 

4. axióm: Mají-li dvě různé roviny α, β společný bod P , pak mají i společnou přímku p a P 

leží na p. Symbolicky: ∀α, β, α ≠ β : P ∈ α ∩ β ⇒ ∃! p : P ∈ p ∧ α ∩ β = p. 

5. axióm: Ke každé přímce p lze bodem P , který na ní neleží, vést jedinou přímku p ′ rovnoběžnou 

s p. Symbolicky: ∀P, p : P /∈ p ⇒ ∃! p ′ : p ′ ||p ∧ P ∈ p ′ . 

Uvedených pět axiómů tvoří základ, ale museli bychom je doplnit o další axiómy, aby systém 

dovoloval vybudování klasické geometrie. Není však cílem tohoto textu uvést úplný přehled 

axiómů a vět prostorové geometrie. Zaměříme se jen na takové vztahy, které budeme přímo 

využívat v dalším výkladu. 

1.2 Určování odchylek 

V rovině umíme určit odchylku přímek, které jsou různoběžné. Protože se zabýváme prostorovými 

vztahy, nadefinujeme si i odchylku dvou mimoběžek a ukážeme si, jak lze určit odchylku 

dvou rovin. 

5

1.3. Kritéria rovnoběžnosti 6 

1.2.1 Odchylka mimoběžek 

1. V prostoru jsou dány dvě mimoběžky a, 

b. 

2. Libovolným bodem M vedeme přímku a ′ 

rovnoběžnou s přímkou a a přímku b ′ rovnoběžnou 

s přímkou b. 

3. Odchylka mimoběžek a, b je rovna odchylce 

přímek a ′ , b ′ . Obrázek 1.1: 

1.2.2 Odchylka dvou rovin 

Uvedeme dva způsoby, jak určit odchylku dvou různoběžných rovin α a β. 

1. způsob - obr. 1.2 

Obrázek 1.2: Obrázek 1.3: 

1. Sestrojíme průsečnici p rovin α a β. 

2. Sestrojíme rovinu γ kolmou na p. 

3. Sestrojíme průsečnici a rovin α a γ a průsečnici b rovin β a γ. 

4. Odchylka ϕ přímek a, b je odchylkou rovin α a β. 

2. způsob - obr. 1.3 

1. Libovolným bodem M vedeme kolmici n k rovině α. 

2. Stejným bodem M vedeme kolmici n ′ k rovině β. 

3. Odchylka přímek n, n ′ je odchylkou rovin α a β. 

1.3 Kritéria rovnoběžnosti 

Věta 1.1 Kritérium rovnoběžnosti přímky s rovinou. Přímka p je rovnoběžná s rovinou 

α, právě když existuje přímka p ′ ležící v rovině α, rovnoběžná s přímkou p – obr. 1.4.

1.4. Kritéria kolmosti 7 

Věta 1.2 Kritérium rovnoběžnosti dvou rovin. Rovina α je rovnoběžná s rovinou β, 

právě když existují různoběžky a, b ležící v rovině α a rovnoběžné s rovinou β – obr. 1.5. 


1.4 Kritéria kolmosti 

Věta 1.3 Kritérium kolmosti přímky a roviny. Přímka p je kolmá k rovině α, jestliže je 

kolmá ke dvěma různoběžkám a, b ležícím v rovině α – obr. 1.6. 

Věta 1.4 Kritérium kolmosti dvou rovin. Rovina α je kolmá k rovině β, jestliže v rovině 

α existuje přímka p kolmá k rovině β (tj. kolmá ke dvěma různoběžkám a, b ležícím v rovině β) 

– obr. 1.7. 


1.5 Otáčení v prostoru 

Transformacím bude věnována celá kapitola. Nyní si pouze připomeneme základní vlastnosti 

otáčení (rotace), protože otáčení budeme potřebovat při studiu zobrazovacích metod.

1.6. Dělící poměr 8 

Popíšeme otáčení v prostoru okolo osy o o úhel ϕ. Body osy otáčení jsou samodružné (zobrazí 

se samy na sebe). Bod A se otáčí po kružnici k. Určíme střed S kružnice k, poloměr r 

a rovinu ρ, ve které kružnice k leží - obr. 1.8. 

• Rovina otáčení ρ prochází bodem A a je kolmá k ose otáčení o. 

• Střed otáčení S je průsečíkem osy o s rovinou ρ. 

• Poloměr otáčení r je velikost úsečky AS, píšeme r = |AS|. 


Příklad 1.1 Jsou dány různoběžné roviny α a π, v rovině α je dán bod A. Napíšeme postup 

pro otočení bodu A do roviny π - obr. 1.9. 

Řešení: 

1. Osou otáčení o je průsečnice rovin α a π (o = α ∩ π). 

2. Rovina otáčení ρ je kolmá k ose o a prochází bodem A (ρ ⊥ o ∧ A ∈ ρ). 

3. Střed otáčení S získáme jako průsečík osy o a roviny ρ (S = o ∩ ρ). 

4. Velikost úsečky SA je poloměr otáčení (r = |SA|). 

□ 

1.6 Dělící poměr 

Na orientované přímce p jsou dány dva různé body A, B. Bod C ≠ B je libovolný bod přímky 

p. Dělící poměr bodu C vzhledem k bodům A, B je číslo 

λ = (A, B, C) = d( −→ AC) : d( −→ BC), 

kde d( −→ AC), d( −→ BC) jsou orientované délky příslušných úseček. 

Například je-li bod C středem úsečky AB, jeho dělící poměr vzhledem k bodům A, B je 

λ = −1, což plyne ze vztahu d( −→ AC) = −d( −→ BC). 

Obráceně ke každému číslu λ ≠ 1 můžeme sestrojit na dané orientované přímce AB bod, 

jehož dělící poměr vůči bodům A, B je dané číslo λ.

1.7. Kontrolní otázky 9 

1.7 Kontrolní otázky 

1.1 Popište, jak lze určit odchylku dvou rovin. 

1.2 Uveďte kritérium rovnoběžnosti přímky a roviny a kritérium rovnoběžnosti dvou rovin. 

1.3 Uveďte kritérium kolmosti přímky a roviny a kritérium kolmosti dvou rovin. 

1.4 Proč nemůže dělící poměr podle uvedené definice nabývat hodnoty 1?

Kapitola 2 

Nevlastní elementy 

2.1 Úvodní úvaha 

Je dána přímka q a bod P , který na této přímce neleží. Bodem P prochází přímka p (obr.2.1). 

Otáčíme přímkou p kolem bodu P a sestrojujeme průsečíky přímky p s přímkou q. 

Obrázek 2.1: 

V určitém okamžiku se přímka p dostane do speciální polohy (p ‖ q), kdy průsečík neexistuje. 

Nyní nastávají dvě možnosti: buď ve svých úvahách budeme uvádět tento případ zvlášť, nebo 

si pomůžeme tím, že i pro tuto situaci zavedeme „průsečík a budeme rovnoběžky považovat 

za přímky, které mají společný bod. Tento průsečík, který ovšem nemůžeme zobrazit, nazveme 

nevlastním bodem. 

2.2 Nevlastní bod, přímka a rovina 

Definice 2.1 Všechny navzájem rovnoběžné přímky v prostoru mají společný právě jeden bod, 

který nazýváme nevlastním bodem. (Někdy říkáme, že rovnoběžné přímky mají stejný směr 

- nahradili jsme tedy pojem směr pojmem nevlastní bod.) - obr. 2.2 

Podobnou úvahu jako v obr. 2.1 můžeme provést pro dvě roviny a vyslovíme další definice: 

10



Definice 2.2 Všechny navzájem rovnoběžné roviny v prostoru mají společnou právě jednu 

přímku, kterou nazýváme nevlastní přímkou - obr. 2.3. 

Definice 2.3 

Nevlastní rovina je množina všech nevlastních bodů a nevlastních přímek. 

Nevlastní útvary označujeme stejně jako vlastní, pouze připojujeme index ∞. Tedy např. 

A ∞ je nevlastní bod, p ∞ je nevlastní přímka apod. 

Euklidovský prostor obsahuje pouze vlastní útvary. Jestliže k němu přidáme právě zavedené 

nevlastní body, přímky a roviny, dostaneme nový prostor, který nazýváme projektivně 

rozšířený euklidovský prostor (nebo zkráceně rozšířený euklidovský prostor). 

V rozšířeném euklidovském prostoru platí pro vlastní útvary všechny axiomy a věty, které 

platily v euklidovském prostoru. Pro nevlastní útvary musíme předpokládat platnost dalších 

tvrzení o incidenci vlastních a nevlastních útvarů: 

• Na každé vlastní přímce leží právě jeden nevlastní bod. 

• V každé vlastní rovině leží právě jedna nevlastní přímka. 

• Nevlastní body všech vlastních přímek jedné roviny leží na nevlastní přímce této roviny. 

Poznámka 2.1 Nevlastní bod na vlastní přímce značíme A ∞ a někdy připojujeme k příslušné 

přímce šipku, což ale nesmí vést k domněnce, že na vlastní přímce existují dva různé nevlastní 

body. Vlastní přímka má jediný nevlastní bod, neboť patří jednomu systému navzájem rovnoběžných 

přímek. Dvě rovnoběžné přímky mají jeden společný nevlastní bod. 


2.1 Definujte nevlastní bod přímky. 

2.2 Kolik nevlastních bodů leží na jedné přímce (rozlište přímku vlastní a nevlastní)? 

2.3 Je pravdivé tvrzení, že v rozšířené euklidovské rovině mají dvě různé přímky právě jeden 

společný bod? Je toto trvzení pravdivé i pro rozšířený euklidovský prostor?

Kapitola 3 

Elementární plochy a tělesa 

3.1 Základní pojmy 

Elementárními plochami budeme rozumět jehlanovou, hranolovou, kuželovou, válcovou a kulovou 

plochu a elementárními tělesy jehlan, hranol, kužel, válec a kouli. Elementární tělesa znáte 

z předchozího studia na střední škole. Zde je jen dáme do souvislostí s nově definovanými pojmy. 

3.1.1 Jehlanová plocha, jehlan 

Jehlanová plocha je určena rovinnou lomenou čárou - polygonem c (c ⊂ σ) a bodem V , který 

neleží v rovině polygonu (V ∉ σ), a je tvořena přímkami, které protínají polygon c a procházejí 

bodem V - obr. 3.1 a). 

Je-li polygon uzavřený, pak množina přímek, které procházejí daným bodem V a protínají 

vnitřek polygonu nebo polygon, se nazývá jehlanový prostor. Přímky určené vrcholem V a 

vrcholy polygonu jsou hrany jehlanové plochy. 

Rovina, která prochází vrcholem, se nazývá vrcholová rovina. 

Jehlan je průnik jehlanového prostoru a prostorové vrstvy určené rovinou σ řídícího polygonu 

a vrcholové roviny σ ′ ‖ σ - obr. 3.1 c). ) Výška jehlanu je vzdálenost vrcholu V od roviny 

podstavy. Má-li podstava střed S a leží-li vrchol V na kolmici vztyčené v bodě S k rovině 

podstavy, nazýváme jehlan kolmý a SV je jeho osa. V opačném případě je jehlan kosý. 

3.1.2 Hranolová plocha, hranol 

Hranolová plocha je určena rovinnou lomenou čárou - polygonem c (c ⊂ σ) a směrem s, který 

nenáleží dané rovině (s ̸‖ σ), a je tvořena přímkami, které protínají polygon c a jsou směru s - 

obr. 3.1b). 

Je-li polygon uzavřený, pak množina přímek směru s, které protínají polygon nebo vnitřek 

polygonu, se nazývá hranolový prostor. Přímky určené vrcholy polygonu a směru s jsou hrany 

hranolové plochy. V projektivním rozšíření euklidovského prostoru lze definovat hranolovou 

plochu jako speciální případ jehlanové plochy, jejímž vrcholem je nevlastní bod. Vrcholovou 

rovinou je každá rovina směru s. 

Hranol je průnik hranolového prostoru a prostorové vrstvy určené rovinou σ řídícího polygonu 

a roviny σ ′ ‖ σ - obr. 3.1d). Výška hranolu je vzdálenost rovin podstav. Jsou-li pobočné 

12

3.1. Základní pojmy 13 

hrany kolmé na roviny podstav, nazýváme hranol kolmý a spojnice středů podstav je jeho osou 

(pokud existuje). V opačném případě je hranol kosý. Hranol, jehož podstavou je rovnoběžník, 

nazýváme rovnoběžnostěn. 


3.1.3 Kuželová plocha, kužel 

Kuželová plocha je určena rovinnou křivku k (k ⊂ σ) a bodem V , který neleží v rovině dané 

křivky (V ∉ σ), a je tvořena přímkami, které protínají křivku k a procházejí bodem V - obr. 

3.2 a). 

Je-li křivka k uzavřená, pak množina přímek, které procházejí daným bodem V a protínají 

křivku nebo vnitřek křivky, se nazývá kuželový prostor. Přímka určená vrcholem V a bodem 

křivky k je površka kuželové plochy. 

Rovina, která prochází vrcholem, se nazývá vrcholová rovina. 

Kužel je průnik kuželového prostoru a prostorové vrstvy určené rovinou σ řídícího polygonu 

a vrcholové roviny σ ′ ‖ σ - obr. 3.2 c). 

Je-li řídící křivkou kuželové plochy kružnice (řídící kružnice), kuželová plocha se nazývá 

kruhová. Jestliže je spojnice středu S řídící kružnice k a vrcholu V kolmá na rovinu σ, pak 

nazýváme kuželovou plochu kolmou nebo rotační a přímku SV osou kuželové plochy. Rotační 

kuželovou plochu můžeme také získat rotací přímky, která protíná osu otáčení a není k ní kolmá. 

Není-li přímka SV kolmá na rovinu řídící kružnice, nazývá se kuželová plocha kosá. Podobně 

kolmý nebo rotační kužel má osu kolmou k rovině podstavy na rozdíl od kosého kužele. 

3.1.4 Válcová plocha, válec 

Válcová plocha je určena rovinnou křivkou k (k ⊂ σ) a směrem s, který nenáleží dané rovině 

(s ̸‖ σ), a je tvořena přímkami, které protínají křivku k a jsou směru s - obr. 3.2 b).


Je-li křivka k uzavřená, pak množina přímek směru s, které protínají křivku nebo procházejí 

vnitřním bodem křivky, se nazývá válcový prostor. Přímka určená bodem křivky k a směru 

s je površka. Podobně jako u hranolové plochy, můžeme v projektivním rozšíření euklidovského 

prostoru definovat válcovou plochu jako speciální případ kuželové plochy, jejímž vrcholem je 

nevlastní bod. Vrcholovou rovinou je každá rovina směru s. 

Válec je průnik válcového prostoru a prostorové vrstvy určené rovinou σ řídícího polygonu 

a roviny σ ′ ‖ σ - obr. 3.2 d). 

Je-li řídící křivkou válcové plochy regulární kuželosečka, získáme eliptickou, parabolickou 

či hyperbolickou válcovou plochu. Jestliže je řídící křivkou kružnice, nazývá se válcová plocha 

kruhová. Jestliže jsou površky kolmé na rovinu řídící kružnice, dostáváme kolmou kruhovou 

neboli rotační válcovou plochu, v opačném případě je plocha kosá. 

Poznámka 3.1 Každá křivka (podle naší definice rovinná) na válcové nebo kuželové ploše 

může být řídící křivkou této plochy. Řezem rotační kuželové plochy rovinou může být, podle 

polohy roviny řezu, i jiná kuželosečka. To znamená, že zvolíme-li tuto kuželosečku jako řídící 

křivku, dostaneme opět rotační kuželovou plochu. Nemá tedy smysl, na rozdíl od válcových 

ploch, rozlišovat hyperbolickou nebo parabolickou kuželovou plochu od eliptické kuželové plochy. 

3.1.5 Kulová plocha, koule 

Kulová plocha je množina všech bodů, které mají od daného bodu S vzdálenost rovnu danému 

kladnému číslu r. Koulí rozumíme množinu všech bodů, které mají od daného bodu S 

vzdálenost menší nebo rovnu danému kladnému číslu r. 


3.1 Popište a načrtněte pravidelný trojboký jehlan a pravidelný čtyřboký hranol. 

3.2 Definujte kosý kruhový válec. 

3.3 Vysvětlete rozdíl mezi koulí a kulovou plochou.

Kapitola 4 

Základy promítání 

4.1 Úvod 

Deskriptivní geometrie se zabývá studiem takových zobrazení, kterými můžeme zobrazit prostorové 

útvary do roviny a naopak. Zpravidla požadujeme, aby tato zobrazení byla vzájemně 

jednoznačná. Vzájemně jednoznačným zobrazením v deskriptivní geometrii říkáme zobrazovací 

metody. 

Protože deskriptivní geometrie vznikla z potřeb praxe, je důležité, aby bylo možné snadno 

vyčíst velikost objektů, jejich tvar a vzájemnou polohu jednotlivých částí. Další požadavky se 

týkají názornosti a snadného řešení stereometrických úloh. 

Procesu našeho vidění se nejvíce blíží středové promítání a jeho speciální případ lineární 

perspektiva. Tyto zobrazovací metody jsou velmi názorné a často se s nimi setkáváme 

v situacích, kdy je třeba reálné zobrazení světa, například v umění nebo architektuře. Nevýhodou 

středového promítání je složitost konstrukcí a obtíže s měřením délek. Proto se v technické 

praxi více používají zobrazovací metody, které můžeme označit společným názvem rovnoběžná 

promítání. V následujícím textu se tedy velmi krátce zmíníme o principech středového promítání, 

ale podrobněji se budeme zabývat promítáním rovnoběžným a jeho speciálním případem 

- pravoúhlým promítáním. 

4.2 Středové promítání 

Zvolme v prostoru rovinu π, na kterou budeme zobrazovat - budeme jí říkat průmětna a bod 

S (vlastní), který neleží v rovině π. Bod S se nazývá střed promítání. Libovolný bod A 

v prostoru (různý od bodu S) zobrazíme do roviny π následujícím způsobem: Body S a A 

proložíme přímku p. Přímka p se nazývá promítací přímka. Průsečík A ′ přímky p s rovinou π 

je středovým průmětem bodu A do roviny π. Podobně sestrojíme bod B ′ jako středový průmět 

bodu B - obr. 4.1. 

Vlastnosti středového promítání 

1. Středovým průmětem bodu různého od středu promítání je bod. (Bod S ve středovém 

promítání nemůžeme zobrazit.) 

15

4.3. Rovnoběžné promítání 16 

2. Středovým průmětem přímky, která neprochází středem promítání S, je přímka. Středovým 

průmětem přímky procházející středem promítání S je bod. 

3. Středovým průmětem roviny procházející středem promítání S je přímka. Středovým 

průmětem roviny, která neprochází středem promítání S, je celá průmětna. 

4. Středovým průmětem bodu A ležícího na přímce k je bod A ′ ležící na středovém průmětu 

k ′ přímky k. Obecně leží-li bod na nějaké čáře, pak jeho průmět leží na průmětu té čáry. 

Říkáme, že se zachovává incidence. 

Poznámka 4.1 Pokud budeme pracovat s body z projektivního rozšíření prostoru, zjistíme, 

že ve středovém promítání může být obrazem vlastního bodu bod nevlastní a naopak obrazem 

nevlastního bodu bod vlastní. Načrtněte si takovou situaci a uveďte vhodný reálný příklad 

(např. zobrazení železničních kolejí). 


4.3 Rovnoběžné promítání 

Podobně jako ve středovém promítání zvolíme v rovnoběžném promítání rovinu π, na kterou 

budeme zobrazovat, a které říkáme průmětna. Dále zvolíme přímku s, která není rovnoběžná 

s rovinou π. Říkáme, že přímka s nám určuje směr promítání. Rovnoběžný průmět A ′ bodu 

A získáme tak, že bodem A vedeme přímku p (nazýváme ji opět promítací přímka), která je 

rovnoběžná s přímkou s a najdeme její průsečík s rovinou π. Podobně najdeme průmět bodu 

B - obr. 4.2. 

Pokud použijeme pojmy z kapitoly o nevlastních elementech, můžeme říct, že rovnoběžné 

promítání je speciální případ středového promítání, kde středem promítání je nevlastní bod. 

Vlastnosti rovnoběžného promítání 

1. Rovnoběžným průmětem (vlastního) bodu je (vlastní) bod.

4.4. Pravoúhlé promítání 17 

2. Rovnoběžným průmětem přímky, která není směru promítání, je přímka. Rovnoběžným 

průmětem přímky, která je směru promítání, je bod. 

3. Rovnoběžným průmětem roviny, která je směru promítání, je přímka. Rovnoběžným průmětem 

roviny, která není směru promítání, je celá průmětna. 

4. Rovnoběžným průmětem bodu A ležícího na přímce k je bod A ′ ležící na rovnoběžném 

průmětu k ′ přímky k. Obecně leží-li bod na nějaké čáře, pak jeho průmět leží na průmětu 

té čáry. 

5. Rovnoběžným průmětem různoběžek a, b jsou různoběžné přímky nebo přímky splývající, 

pokud a, b nejsou směru promítání. Jestliže je jedna z přímek a, b směru promítání, pak 

rovnoběžným průmětem různoběžek a, b je přímka a na ní bod. 

6. Rovnoběžnost se zachovává, tj. rovnoběžné přímky se zobrazí na rovnoběžné nebo splývající 

přímky (nebo na dva body), rovnoběžné úsečky na rovnoběžné úsečky apod. 

7. Rovnoběžným průmětem rovnoběžných a shodných úseček jsou rovnoběžné a shodné 

úsečky (popř. dva body). 

8. Rovnoběžným průmětem útvaru ležícího v rovině rovnoběžné s průmětnou je útvar s ním 

shodný. 

9. Dělící poměr se v rovnoběžném promítání zachovává, tj. například střed úsečky se zobrazí 

na střed úsečky. 

Druhy rovnoběžného promítání 

Podle vztahu směru promítání vzhledem k průmětně rozlišujeme dva druhy rovnoběžného promítání. 

Jestliže směr promítání je kolmý k průmětně, pak hovoříme o pravoúhlém (nebo také 

o kolmém či ortogonálním) promítání. Pokud směr promítání není kolmý k průmětně, mluvíme 

o kosoúhlém promítání. Připomeňme, že jsme vyloučili případ, kdy směr promítání je 

rovnoběžný s průmětnou. 

4.4 Pravoúhlé promítání 

Vlastnosti, které jsme uvedli pro rovnoběžné promítání, doplníme dvěma větami, které platí 

jen pro pravoúhlé promítání. 

Věta 4.1 (Věta o pravoúhlém průmětu pravého úhlu) Pravoúhlým průmětem pravého úhlu 

je pravý úhel, jestliže alespoň jedno jeho rameno je rovnoběžné s průmětnou a druhé není na 

průmětnu kolmé. 

Věta 4.2 Velikost pravoúhlého průmětu A ′ B ′ úsečky AB je menší nebo rovna velikosti úsečky 

AB, tj. |A ′ B ′ | ≤ |AB|. 

4.5 Středová kolineace 

Jsou dány dvě různé roviny α a α ′ a bod S, který neleží v žádné z rovin α a α ′ . Středová 

kolineace je geometrická příbuznost, kdy bodu jedné roviny odpovídá jeho středový průmět 

z bodu S do druhé roviny. Průsečnice o rovin α a α ′ se nazývá osa kolineace (obr. 4.3).

4.5. Středová kolineace 18 


Vlastnosti středové kolineace 

Uvedeme vlastnosti středové kolineace, které vyplývají z vlastností středového promítání. 

1. Bodu odpovídá bod a přímce přímka. 

2. Přímky, které si odpovídají ve středové kolineaci, se protínají na ose kolineace nebo jsou 

s ní rovnoběžné, což ale znamená, že mají společné nevlastní body. 

3. Body osy kolineace jsou samodružné, tj. vzor a obraz splývají. 

4. Středová kolineace zachovává incidenci. To znamená, že jestliže bod A leží na přímce b, 

pak pro jejich obrazy A ′ , b ′ opět platí A ′ ∈ b ′ . 

5. Body, které si odpovídají ve středové kolineaci, leží na přímce procházející středem kolineace. 

Poznámka 4.2 Je nutné si uvědomit, že středová kolineace obecně nezachovává rovnoběžnost 

a že vlastnímu bodu může odpovídat bod nevlastní a naopak. Také dělící poměr tří kolineárních 

bodů se obecně ve středové kolineaci nezachovává. 

Středová kolineace v rovině 

Protože se zabýváme zobrazováním trojrozměrného prostoru na rovinu, zajímá nás, co se stane, 

promítneme-li středovou kolineaci do roviny. 

Promítneme rovnoběžně obě roviny α, α ′ a střed promítání S do průmětny π tak, aby směr 

promítání nebyl rovnoběžný s žádnou z rovin α a α ′ (tj. žádná z rovin se nezobrazí jako přímka). 

Odpovídající si body A a A ′ promítnuté do π leží opět na přímce procházející průmětem středu 

kolineace. Takto získanou příbuznost v rovině nazveme středovou kolineací v rovině - obr. 

4.4. 

Vlastnosti, které jsme uvedli pro středovou kolineaci mezi rovinami, platí také pro středovou 

kolineaci v rovině. 

Znalost středové kolineace využijeme např. při sestrojování řezů na jehlanu a kuželi.


Středová kolineace v rovině je určena středem S, osou o a párem odpovídajících si bodů A, 

A ′ (body A, A ′ , S leží na jedné přímce). Pro sestrojování obrazů bodů ve středové kolineaci 

jsou nejdůležitější tyto tři vlastnosti: 

1. Středová kolineace zachovává incidenci. 

2. Přímky, které si odpovídají ve středové kolineaci, se protínají na ose kolineace nebo jsou 

s ní rovnoběžné. 

3. Body, které si odpovídají, leží na přímce procházející středem kolineace. 

Příklad 4.1 Středová kolineace v rovině je určena středem S, osou o a párem odpovídajících 

si bodů A, A ′ - obr. 4.5. Sestrojíme obraz bodu B v kolineaci. 

Řešení: (obr. 4.6) 

1. Spojíme bod B se vzorem bodu, pro který známe jeho obraz, tj. v našem případě s bodem 

A - dostaneme přímku p. 

2. Najdeme obraz p ′ přímky p (p a p ′ se protínají na ose a přímka p ′ prochází bodem A ′ - 

vlastnost 2. a 1.) 

3. Protože body, které si odpovídají, leží na přímce procházející středem kolineace- vlastnost 

3., sestrojíme přímku SB. 

4. Bod B ′ leží v průsečíku přímek SB a p ′ . 


□ 

Jak jsme již uvedli, obrazem vlastního bodu ve středové kolineaci nemusí vždy být vlastní 

bod. Stejně tak se některé nevlastní body zobrazí na vlastní body. Vzory a obrazy nevlastních 

bodů nazýváme úběžníky. Vzor nevlastní přímky se nazývá úběžnice vzorů a obraz nevlastní 

přímky se nazývá úběžnice obrazů. 

Nevlastní přímka má s osou o společný nevlastní bod (nevlastní bod osy o). Přímky, které si 

odpovídají v kolineaci se protínají na ose, pokud je tento bod nevlastní, pak jsou odpovídající 

si přímky rovnoběžné. Tedy obě úběžnice jsou rovnoběžné s osou kolineace.



si bodů A, A ′ - obr. 4.7. Sestrojíme úběžnici obrazů. 


1. Zvolíme libovolný bod V ∞ na nevlastní přímce. 

2. Najdeme obraz V ′ nevlastního bodu V ∞ (bod V ′ je vlastní). 

3. Bod V ′ leží na úběžnici obrazů v ′ a ta je rovnoběžná s osou o. 

4. Podobně lze sestrojit úběžnici vzorů. Úběžnice vzorů je rovnoběžná s osou o a prochází 

vzorem bodu U ′ ∞ (bod U ′ ∞ je libovolný bod nevlastní přímky). 



si přímek p, p ′ - obr. 4.9. Sestrojíme obě úběžnice. 


1. Označíme V ∞ nevlastní bod přímky p. 

2. Najdeme obraz V ′ nevlastního bodu V ∞ (V ′ ∈ p ′ ) a sestrojíme úběžnici obrazů v ′ (v ′ ‖ 

o, V ′ ∈ v ′ ). 

3. Dále označíme bod U ′ ∞ nevlastní bod přímky p ′ . 

4. Najdeme vzor U nevlastního bodu U ′ ∞ (U ∈ p) a sestrojíme úběžnici vzorů v (v ‖ o, U ∈ 

u). 

□ 

Ve středové kolineaci v rovině je vzdálenost středu od jedné úběžnice rovna vzdálenosti 

druhé úběžnice od osy kolineace. Podíváme-li se znovu na obrázek 4.10, pak toto tvrzení plyne 

z rovnoběžníka SUMV ′ . 

Středová kolineace v rovině se nazývá involutorní, když pro všechny body X, Y platí: 

jestliže X = Y ′ , pak Y = X ′ . V involutorní kolineaci úběžnice splývají a půlí vzdálenost středu 

kolineace od osy. 

Nechť body A, A ′ si odpovídají ve středové kolineaci, bod Ā je průsečík přímky AA′ s osou 

′ (A′ AĀ) 

o. Pak dvojpoměr (A AĀS) = je konstantní pro všechny páry odpovídajících si bodů. 

(A ′ AS) 

′ 

Číslo k = (A AĀS) se nazývá charakteristika středové kolineace, charakteristika involutorní 

kolineace je k = −1. 

□

4.6. Osová afinita 21 


4.6 Osová afinita 

Jsou dány dvě různé roviny α a α ′ a směr s, který není rovnoběžný s žádnou z rovin α a α ′ . 

Osová afinita je geometrická příbuznost, kdy bodu jedné roviny odpovídá jeho rovnoběžný 

průmět ve směru s do druhé roviny. 

Průsečnice rovin α a α ′ se nazývá osa afinity (obr. 4.11). 


Vlastnosti osové afinity 

(vyplývají z rovnoběžného promítání) 

Vlastnosti 1.- 5. jsou podobné vlastnostem pro kolineaci, ale všimněte si pozorně vlastností 

6. a 7. 

1. Bodu odpovídá bod a přímce přímka. 

2. Přímky, které si odpovídají v osové afinitě, se protínají na ose afinity nebo jsou s ní 

rovnoběžné.

4.6. Osová afinita 22 

3. Body osy afinity jsou samodružné. 

4. Osová afinita zachovává incidenci.(To znamená, že jestliže bod A leží na přímce b, pak 

pro jejich průměty A ′ , b ′ opět platí A ′ ∈ b ′ .) 

5. Body, které si odpovídají v osové afinitě leží na rovnoběžce se středem promítání. 

6. Osová afinita zachovává rovnoběžnost. 

7. Osová afinita zachovává dělící poměr. 

Osová afinita v rovině 

Podobně jako kolineaci promítneme rovnoběžně i afinitu. 

Promítneme rovnoběžně obě roviny α, α ′ a směr promítání s do průmětny π tak, aby směr 

promítání u do roviny π nebyl rovnoběžný s žádnou z rovin α a α ′ (tj. žádná z rovin se nezobrazí 

jako přímka) a aby nebyl rovnoběžný se směrem s (dostali bychom identitu). Odpovídající si 

body A a A ′ promítnuté do π leží na přímce rovnoběžné s promítnutým směrem s. 

Takto získanou příbuznost nazveme osovou afinitou v rovině - obr. 4.12. 

Uvedené vlastnosti osové afinity mezi rovinami budou platit i pro osovou afinitu v rovině. 

Osovou afinitu využijeme při sestrojování řezů na hranolu a kuželi a při otáčení v Mongeově 

projekci a axonometrii. 

Nejčastější určení osové afinity je osou o a párem odpovídajících si bodů A a A ′ (tím je 

určen směr afinity). Opět zopakujeme tři vlastnosti, které využijeme při sestrojování obrazu 

nebo vzoru daného bodu: 

1. Osová afinita zachovává incidenci 

2. Přímky, které si odpovídají v osové afinitě, se protínají na ose afinity nebo jsou s ní 

rovnoběžné. 

3. Body, které si odpovídají, leží na rovnoběžce se směrem afinity. 

Příklad 4.4 Osová afinita v rovině je určena osou o a párem odpovídajících si bodů A, A ′ - 

obr. 4.13. Sestrojíme obraz bodu B v afinitě. 


1. Spojíme bod B s bodem A - dostaneme přímku p. (Obecně se vzorem bodu, pro který 

známe jeho obraz.) 

2. Najdeme obraz p ′ přímky p (p a p ′ se protínají na ose a přímka p ′ prochází bodem A ′ - 

vlastnost 2 a 1) 

3. Protože body, které si odpovídají, leží na přímce směru afinity a tento směr určuje přímka 

AA ′ (vlastnost 3), sestrojíme přímku k rovnoběžnou s přímkou AA ′ a procházející bodem 

B. 

4. Bod B ′ leží v průsečíku přímek k a p ′ . 

□

4.7. Kružnice v osové afinitě a středové kolineaci 23 


Poznámka 4.3 Osová afinita může být určena i jiným způsobem než osou a párem odpovídajících 

bodů, např. osou, směrem a párem odpovídajících si přímek (které se protínají na 

ose) nebo dvěma páry odpovídajících si přímek. Stejně i kolineace může být určena jinak než 

středem, osou a párem odpovídajících si bodů. 

Osovou afinitu můžeme chápat jako speciální případ středové kolineace, kdy střed kolineace 

je nevlastním bodem. Vztah mezi afinitou a kolineací nám přiblíží schéma na obrázku 4.16. 

4.7 Kružnice v osové afinitě a středové kolineaci 

Ve středové kolineaci odpovídá kuželosečce k kuželosečka k ′ (nemusí být stejného typu) a platí: 

1. Bodům a tečnám vzoru odpovídají body a tečny obrazu, 

2. Středu kuželosečky k obecně neodpovídá střed kuželosečky k ′ , 

3. Průměru kuželosečky k obecně neodpovídá průměr kuželosečky k ′ , 

4. Sdruženým průměrům kuželosečky k neodpovídají sdružené průměry kuželosečky k ′ . 

Jestliže kružnice k nemá s úběžnicí u žádný společný bod, pak se všechny její body zobrazí 

na body vlastní a obrazem kružnice k ve středové kolineaci je elipsa; jestliže se kružnice k 

dotýká úběžnice u, pak se tento dotykový bod zobrazí na nevlastní bod a obrazem kružnice k 

ve středové kolineaci je parabola; jestliže kružnice k úběžnici u protíná, pak obrazem kružnice 

k ve středové kolineaci je hyperbola, která má dva nevlastní body (viz obr. 4.15). 

V osové afinitě se všechny vlastní body zobrazí opět na vlastní body, kuželosečce k odpovídá 

kuželosečka k ′ , je stejného typu a platí: 

1. Bodům a tečnám vzoru odpovídají body a tečny obrazu, 

2. Středu kuželosečky k odpovídá střed kuželosečky k ′ , 

3. Průměru kuželosečky k odpovídá průměr kuželosečky k ′ ,


Obrázek 4.15: 

4. Sdruženým průměrům kuželosečky k odpovídají sdružené průměry kuželosečky k ′ . 

Obrazem kružnice k v osové afinitě je tedy elipsa. 


4.1 Vyslovte větu o pravoúhlém průmětu pravého úhlu. 

4.2 Jakou délku může mít (v porovnání s délkou zobrazované úsečky) průmět úsečky v pravoúhlém 

promítání a jakou v kosoúhlém? 

4.3 Rovnoběžné promítání zachovává dělící poměr. Je pravda, že obrazem středu úsečky je 

v rovnoběžném promítání střed úsečky, která je průmětem dané úsečky? 

4.4 Jakou vlastnost mají body, které leží na ose afinity nebo kolineace? 

4.5 Jakou vlastnost mají body úběžnic kolineace?


Obrázek 4.16:

Kapitola 5 

Mongeovo promítání 

5.1 Úvod 

Mongeovo promítání je pravoúhlé promítání na dvě navzájem kolmé průmětny. Jeho výhodou je 

snadné řešení stereometrických úloh, nevýhodou může být menší názornost a složitější orientace 

ve dvou pohledech na jeden objekt. 

Obrázek 5.1: 

Zvolíme v prostoru dvě navzájem kolmé roviny. 

Rovinu π volíme ve vodorovné poloze - říkáme 

jí půdorysna - a rovinu ν v poloze svislé - nárysna. 

Průsečnici rovin π a ν ztotožníme s osou 

x souřadnicového systému a říkáme jí základnice. 

Osu y volíme v rovině π, tak aby byla 

kolmá k x. Průsečíkem O os x a y prochází osa 

z, leží v rovině ν a je kolmá k osám x, y. V Mongeově 

promítání budeme při vynášení souřadnic 

používat zpravidla levotočivý souřadnicový systém 

– viz obr. 5.2. Při použití pravotočivého 

souřadnicového systému by se kladné souřadnice 

x nanášely vlevo. 

Poznámka 5.1 Pokud bychom chtěli promítat pouze na jednu průmětnu, pak útvar, který 

promítneme, nebude v prostoru jednoznačně určen. Další možností je použít kótované promítání, 

to znamená, že ke každému bodu budeme připisovat jeho vzdálenost od průmětny. 

Toto promítání se používá při řešení střech a při tvorbě map (vstevnice), to znamená většinou 

v případech, kdy není nutné řešit složitější prostorové vztahy. 

5.2 Obraz bodu 

Nejprve kolmo promítneme bod B do půdorysny a průmět označíme indexem 1 - dostaneme bod 

B 1 - obr. 5.2a), potom bod B promítneme do nárysny, průmět označíme indexem 2 a získáme 

26

5.3. Obraz přímky 27 

bod B 2 - obr. 5.2b). Nyní máme dvě možnosti, jak si představit sdružení průmětů. Buď otočíme 

rovinu π kolem osy x tak, aby kladná část osy y splynula se zápornou částí osy z - obr. 5.1 

nebo si představíme nárysnu a půdorysnu jako dvě průhledné folie, které položíme na sebe, tak 

aby se překrývaly průměty osy x 1 a x 2 a bod O 1 a O 2 - obr. 5.2. 

Bod B 1 nazýváme půdorysem a bod B 2 nárysem bodu B. Spojnice nárysu a půdorysu 

téhož bodu je kolmá k základnici a nazývá se ordinála. (Půdorys je vlastně pohled shora a 

nárys je pohled zpředu). 

Z obrázku 5.2 c) je vidět, jak sestrojíme nárys a půdorys bodu, známe-li jeho souřadnice. 

V našem případě jsou všechny tři souřadnice kladné. Nárysu a půdorysu bodu B říkáme sdružené 

průměty bodu B. (Neplést si se sdruženými průměry, ty najdeme u elipsy.) 

Obrázek 5.2: 

Příklad 5.1 Určeme, kde bude ležet nárys a půdorys bodů B, C, D, E, jestliže umístíme každý 

do jiného kvadrantu vymezeného nárysnou a půdorysnou - obr. 5.3. 

Řešení: (obr. 5.4) Bod B, který se nachází nad půdorysnou a před nárysnou, má půdorys pod 

osou a nárys nad osou x 1,2 . 

Bod C leží za nárysnou a nad půdorysnou a oba jeho průměty leží nad osou x 1,2 . 

Nárys i půdorys bodu E ležícího pod půdorysnou a před nárysnou najdeme pod osou x 1,2 . 

Pro bod D, který je za nárysnou a pod půdorysnou platí, že nárys je pod a půdorys nad 

osou x 1,2 . 

□ 

5.3 Obraz přímky 

Z vlastností rovnoběžného promítání víme, že obrazem přímky je buď přímka, nebo bod. Pokud 

přímka p není kolmá k ose x, pak jejím půdorysem a nárysem jsou přímky p 1 a p 2 , které nejsou 

kolmé k ose x 1,2 - obr. 5.5 a 5.6. Jestliže je přímka kolmá k půdorysně je jejím půdorysem 

bod a nárysem přímka kolmá k ose x 1,2 , pro přímku kolmou k nárysně bude nárysem bod 

a půdorysem přímka kolmá k ose x 1,2 . Ve všech těchto případech je přímka svými průměty 

jednoznačně určena.

5.3. Obraz přímky 28 


Je-li přímka kolmá k ose x a přitom není kolmá k žádné průmětně, pak její sdružené průměty 

splývají a jsou kolmé k x 1,2 . Jen v tomto případě není přímka určena svými sdruženými průměty. 

K určení je v tomto případě nutná znalost např. průmětů dvou různých bodů přímky. 

Přímkou, která není kolmá k průmětně, můžeme proložit rovinu kolmou k průmětně. Této 

rovině říkáme promítací rovina přímky. Přímkou můžeme proložit půdorysně promítací 

rovinu kolmou k půdorysně nebo nárysně promítací rovinu kolmou k nárysně. 

Na zvláštní polohy přímky vzhledem k průmětně se podívejme v příkladu 5.2. 


Příklad 5.2 V obrázku 5.7 určíme polohu jednotlivých přímek vzhledem k průmětnám. 

Řešení: Přímky p, q, r jsou kolmé k základnici. Přímka p je navíc kolmá k půdorysně a q 

je kolmá k nárysně. Přímka r není svými průměty jednoznačně určena a musíme ji dourčit 

sdruženými průměty dvou bodů, které na ní leží. Přímka s je rovnoběžná s půdorysnou a přímka 

t s nárysnou, s ′ v půdorysně leží a u je rovnoběžná se základnicí. 

□

5.4. Obraz roviny 29 

Obrázek 5.7: 

Vzájemný vztah přímky a bodu, který na ní leží, je v Mongeově promítání dán větou: 

Věta 5.1 Leží-li bod M na přímce p, pak M 1 ∈ p 1 a M 2 ∈ p 2 . 

Jestliže přímka p je určena svými průměty (tím vylučujeme přímky kolmé k ose x a nejsou 

promítací), pak pro sdružené průměty bodu M a přímky p platí: pokud M 1 ∈ p 1 a M 2 ∈ p 2 , pak 

bod M leží na přímce p. 

Přímka je jednoznačně určena dvěma body. Pro sdružené průměty přímky můžeme vyslovit 

následující větu: 

Věta 5.2 Sdružené průměty přímky p = AB jsou v Mongeově promítání jednoznačně určeny 

průměty dvou jejích bodů A, B. 

Vlastní bod, ve kterém přímka protne průmětnu, nazýváme stopník. Půdorysný stopník 

P je bod, ve kterém přímka protne půdorysnu, nárysný stopník N je bod, ve kterém přímka 

protíná nárysnu - obr. 5.5. 

Pro půdorysný stopník P přímky p platí: P 1 ∈ p 1 , P 2 ∈ p 2 a P 2 ∈ x 1,2 . 

Pro nárysný stopník N přímky p platí: N 1 ∈ p 1 , N 2 ∈ p 2 a N 1 ∈ x 1,2 - obr. 5.6. 

Poznámka 5.2 Přímka, která je rovnoběžná s průmětnou, má jen jeden stopník. 

5.4 Obraz roviny 

Pravoúhlým průmětem roviny, která není kolmá k průmětně, je celá průmětna. Rovinu v Mongeově 

projekci zadáme pomocí sdružených průmětů určujících prvků. Ukažme si nejobvyklejší 

způsoby určení roviny. 

1. Třemi body, které neleží v přímce (nekolineární body) - obr. 5.8. 

2. Dvěma různoběžkami - obr. 5.9. Sdružené průměty průsečíku různoběžek musí ležet 

na ordinále.




3. Dvěma rovnoběžkami - obr. 5.10. Nárysem i půdorysem rovnoběžek jsou opět rovnoběžky 

(mohou ovšem i splývat). 

4. Bodem a přímkou - obr. 5.11. Aby byla rovina určena bodem a přímkou, nesmí bod 

ležet na přímce. 

Speciálním případem je zadání roviny stopami. Stopa roviny ρ je přímka, ve které rovina 

ρ protne průmětnu. Průsečnice roviny ρ s nárysnou se nazývá nárysná stopa a značíme ji n ρ . 

Průsečnice roviny ρ s půdorysnou se nazývá půdorysná stopa a značíme ji p ρ . 

Stopy roviny jsou dvě přímky (rovnoběžné nebo různoběžné). Rovina určená stopami je 

tedy opět určena rovnoběžkami nebo různoběžkami. 

Pro půdorys nárysné stopy n ρ 1 a nárys půdorysné stopy p ρ 2 platí n ρ 1 = p ρ 2 = x 1,2 . Přímky n ρ 2 

a p ρ 1 se protínají na ose x 1,2 - obr. 5.12 nebo jsou obě rovnoběžné s osou x 1,2 . 

Příklad 5.3 V obrázku 5.13 rozhodneme, jakou polohu mají roviny, určené svými stopami, 

vzhledem k průmětnám. 

Řešení: Rovina α je v obecné poloze vzhledem k průmětnám, není kolmá ani rovnoběžná 

s žádnou z průměten. Rovina β je kolmá k nárysně, rovina γ je kolmá k půdorysně. Rovina σ 

je kolmá k ose x a ρ je s x rovnoběžná. Posledním případem je rovina τ, která obsahuje osu x, 

v tomto případě není rovina stopami jednoznačně určena. 

□




Poznámka 5.3 Rovina, která je rovnoběžná s průmětnou, má jen jednu stopu. 

V následujících kapitolách ukážeme 12 základních úloh, pomocí kterých budeme schopni 

řešit složitější konstrukce jako např. sestrojení těles v obecné poloze, jejich průniky či řezy na 

plochách. Každou složitější úlohu pak rozložíme na tyto základní úlohy, které už budeme umět 

řešit (provedeme dekompozici, což je velice důležitý postup plynoucí z analytického geometrického 

myšlení). 

Rozdělíme úlohy na dva typy - polohové a metrické. Polohové úlohy řeší vztahy mezi jednotlivými 

útvary, jako je vzájemná poloha, průnik, rovnoběžnost. Vzdálenosti, velikost objektů, 

kolmost nám pomohou určit úlohy metrické. 

Uvedeme vždy důležité skutečnosti, které budeme využívat, a ukážeme přímo na příkladech 

řešení základních úloh.

5.5. Polohové úlohy 32 

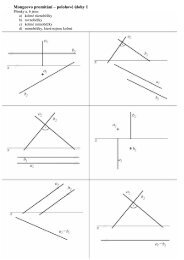
5.5 Polohové úlohy 

5.5.1 Přímka v rovině (základní úloha Z1) 

Při řešení této úlohy je vhodné uvědomit si následující 

fakta: 

• Leží-li přímka v rovině, je se všemi přímkami 

roviny různoběžná nebo rovnoběžná. 

• Stopník přímky ležící v rovině leží na její 

stopě (Půdorysný stopník na půdorysné 

stopě, nárysný stopník na nárysné stopě). 

• Chceme-li sestrojit stopu roviny, určíme 

stopníky dvou přímek ležících v rovině. Půdorysná 

stopa je spojnicí půdorysných stopníků, 

nárysná stopa je spojnicí nárysných 

stopníků. Obrázek 5.14: 


Příklad 5.4 Je dána rovina ρ a jeden průmět přímky k ležící v rovině ρ. Sestrojme druhý 

průmět přímky k. 

a) Rovina ρ je učena přímkami a, b - obr. 5.15. 

b) Rovina ρ je učena stopami - obr. 5.17. 

Řešení: a) obr. 5.16 

1. Sestrojíme průsečík A 1 přímky a 1 a k 1 . 

2. Sestrojíme průsečík B 1 přímky b 1 a k 1 . 

3. Odvodíme druhé průměty bodů A a B. Na přímce a 2 dostaneme bod A 2 a podobně bod 

B 2 .



4. Přímka k 2 je spojnicí bodů A 2 a B 2 . 

b) obr. 5.18 

1. Sestrojíme nárys nárysného stopníku N 2 - průsečík přímky k 2 a stopy n ρ 2. 

2. Sestrojíme nárys půdorysného stopníku P 2 - průsečík přímky k 2 a osy x 1,2 = p ρ 2. 

3. Určíme body N 1 a P 1 , N 1 leží na ose x 1,2 a P 1 na stopě p ρ 1. 

4. Přímka k 1 je spojnicí bodů N 1 a P 1 . 

Hlavní přímky roviny 

Hlavní přímka roviny ρ je přímka, která leží v rovině ρ a je rovnoběžná s průmětnou. 

Horizontální hlavní přímka (hlavní přímka první osnovy) je rovnoběžná s půdorysnou. 

Speciálním případem horizontální hlavní přímky je půdorysná stopa. Všechny horizontální 

hlavní přímky jedné roviny jsou navzájem rovnoběžné – obr. 5.19. 

□ 

Obrázek 5.19: Obrázek 5.20:


Frontální hlavní přímka (hlavní přímka druhé osnovy) je rovnoběžná s nárysnou. Speciálním 

případem frontální hlavní přímky je nárysná stopa. Všechny frontální hlavní přímky 

jedné roviny jsou navzájem rovnoběžné – obr. 5.20. 



Příklad 5.5 Zobrazte nějakou (libovolnou) a) horizontální hlavní přímku roviny ρ - obr. 5.21, 

b) frontální hlavní přímku roviny ρ - obr. 5.23. 

Řešení: a) (obr. 5.22) Horizontální hlavní přímka je rovnoběžná s půdorysnou, proto je její 

nárys rovnoběžný s osou x 1,2 . 

1. Sestrojíme nárys přímky h. (h 2 ||x 1,2 ). 

2. Půdorys přímky h je rovnoběžný se stopou p ρ 1. Použijeme stopník N přímky h. 

Kdyby rovina nebyla určena stopami, odvodili bychom půdorys pomocí průsečíků s jinými 

přímkami roviny. 

b) (obr.5.24) Frontální hlavní přímka je rovnoběžná s nárysnou, proto je její půdorys rovnoběžný 

s osou x 1,2 . 

1. Sestrojíme půdorys přímky f. (f 1 ||x 1,2 ).


2. Nárys přímky f je rovnoběžný se stopou n ρ 2. Použijeme stopník P přímky f. 

Kdyby rovina nebyla určena stopami, odvodili bychom nárys pomocí průsečíků s jinými přímkami 

roviny. 

□ 

Spádové přímky roviny 

Spádová přímka je kolmá na hlavní přímky jednoho systému - obr. 5.25. To znamená, že 

máme dva systémy spádových přímek - spádové přímky kolmé na horizontální hlavní přímky - 

spádové přímky první osnovy a spádové přímky kolmé na frontální hlavní přímky - spádové 

přímky druhé osnovy. 

Příklad 5.6 Sestrojíme spádovou přímku s první osnovy (kolmou k horizontálním hlavním 

přímkám). 

Řešení: (obr. 5.26) Půdorys s 1 spádové přímky je kolmý k půdorysné stopě p ρ 1, což plyne z věty 

o pravoúhlém průmětu pravého úhlu. Najdeme půdorysy stopníků této přímky a odvodíme je 

do nárysu. Nárys s 2 spádové přímky prochází nárysy těchto stopníků. Nárys spádové přímky 

nemá žádnou speciální polohu vůči stopám nebo ose x. 

□ 


5.5.2 Bod v rovině (základní úloha Z2) 

Bod leží v rovině, právě když leží na některé přímce roviny. Chceme-li odvodit druhý průmět 

bodu ležícího v rovině, zvolíme přímku procházející tímto bodem (může to být i přímka hlavní) 

a použijeme řešení úlohy 5.5.1, tj. Z1. Bod leží na odvozené přímce a na ordinále. 

Příklad 5.7 Rovina ρ je určena přímkami a, b. Sestrojme nárys bodu M ležícího v rovině ρ, 

známe-li jeho půdorys - obr. 5.27. 


1. Bodem M 1 vedeme přímku k 1 , tím jsme úlohu převedli na úlohu 5.5.1, tj. Z1.



a) Sestrojíme průsečík A 1 přímky a 1 a k 1 . 

b) Sestrojíme průsečík B 1 přímky b 1 a k 1 . 

c) Odvodíme body A 2 a B 2 . Po ordinále na přímce a 2 dostaneme bod A 2 , na přímce b 2 

dostaneme bod B 2 . 

d) Přímka k 2 je spojnicí bodů A 2 a B 2 . 

2. Bod M 2 najdeme na přímce k 2 a na ordinále vedené bodem M 1 . 

□ 


Příklad 5.8 Rovina ρ je určena stopami. Sestrojme půdorys bodu M ležícího v rovině ρ, 

známe-li jeho nárys - obr. 5.29. 


1. Bodem M 2 vedeme přímku k 2 , tím jsme úlohu převedli na úlohu 5.5.1, tj. Z1. 

a) Sestrojíme nárys nárysného stopníku N 2 - průsečík přímky k 2 a stopy n ρ 2.


b) Sestrojíme nárys půdorysného stopníku P 2 - průsečík přímky k 2 a osy x 1,2 = p ρ 2. 

c) Odvodíme body N 1 a P 1 , N 1 leží na ose x 1,2 a P 1 na stopě p ρ 1. 

d) Přímka k 1 je spojnicí bodů N 1 a P 1 . 

2. Bod M 1 najdeme na přímce k 1 a na ordinále vedené bodem M 2 . 

5.5.3 Rovnoběžné roviny (základní úloha Z3) 

□ 

Při řešení této úlohy je vhodné uvědomit si následující 

fakta: 

• Kritérium rovnoběžnosti přímky a roviny. 

Kritérium rovnoběžnosti dvou rovin. 

• Rovnoběžné roviny mají rovnoběžné 

stopy. 

• Stopy roviny obecně neprochází nárysem 

i půdorysem bodu ležícím v této rovině 

(aby nastal tento případ, musel by bod 

ležet na ose x). Obrázek 5.31: 


Příklad 5.9 Rovina ρ je určena přímkami a, b. Bodem M veďte rovinu σ rovnoběžnou s rovinou 

ρ - obr. 5.32. 

Řešení: (obr.5.33)


1. Bodem M vedeme přímku a ′ rovnoběžnou s přímkou a (a ′ 1||a 1 , a ′ 2||a 2 ). 

2. Bodem M vedeme přímku b ′ rovnoběžnou s přímkou b (b ′ 1||b 1 , b ′ 2||b 2 ). 

3. Přímkami a ′ b ′ je určena rovina σ. 

□ 


Příklad 5.10 Rovina ρ je určena stopami. Bodem M veďte rovinu σ rovnoběžnou s rovinou ρ 

- obr.5.34. Sestrojte stopy roviny σ. 


1. Bodem M vedeme hlavní přímku h rovnoběžnou s půdorysnou stopou roviny ρ (h 1 ||p ρ 1, 

h 2 ||p ρ 2 = x 1,2 ). 

2. Bodem M vedeme hlavní přímku f rovnoběžnou s nárysnou stopou roviny ρ (f 2 ||n ρ 2, 

f 1 ||n ρ 1 = x 1,2 ). 

3. Přímkami h, f je určena rovina σ. 

4. Pro sestrojení stop roviny σ nám stačí nalézt stopník jedné z přímek h f - našli jsme 

půdorysný stopník P přímky f. 

5. Půdorysná stopa roviny σ prochází půdorysným stopníkem a je rovnoběžná s půdorysnou 

stopou roviny ρ. 

6. Nárysná stopa roviny σ je rovnoběžná s nárysnou stopou roviny ρ a protíná se s půdorysnou 

stopou na ose x. 

5.5.4 Průsečík přímky s rovinou (základní úloha Z4) 

Příklad 5.11 Rovina σ je určena přímkami a, b. Sestrojte průsečík přímky p s rovinou σ - obr. 

5.37. 


□


Pro určení průsečíku přímky s rovinou použijeme 

metodu krycí přímky. V rovině σ zvolíme 

přímku s, která se „kryje s přímkou p v 

některém průmětu, tj. leží s přímkou p v jedné 

promítací rovině, a zároveň leží v rovině σ. 

Přímka s je průsečnicí roviny σ a promítací roviny 

přímky p. Průsečík přímky p a s je zároveň 

průsečíkem přímky p s rovinou σ. V průmětně, 

ve které průměty přímek p a s nesplývají, najdeme 

jejich průsečík a odvodíme pomocí ordinály 

do druhé průmětny. Obrázek 5.36: 

1. V rovině σ zvolíme půdorysně krycí přímku s (s 1 = p 1 , s ⊂ σ). 

2. Pomocí průsečíků přímky s s přímkami a, b odvodíme přímku s 2 (úloha 5.5.1, tj. Z1). 

3. Průsečík P 2 přímek p 2 a s 2 je nárysem hledaného průsečíku přímky p s rovinou σ. 

4. Půdorys P 1 průsečíku najdeme na přímce p 1 a na ordinále vedené bodem P 2 . 

□ 


Příklad 5.12 Rovina σ je určena stopami. Sestrojte průsečík přímky p s rovinou σ - obr. 5.39. 


1. V rovině σ zvolíme nárysně krycí přímku s (s 2 = p 2 , s ⊂ σ). 

2. Pomocí stopníků odvodíme přímku s do půdorysu (úloha 5.5.1, tj. Z1). 

3. Průsečík P 1 přímek p 1 a s 1 je půdorysem hledaného průsečíku přímky p s rovinou σ. 

4. Nárys P 2 průsečíku najdeme na přímce p 2 a na ordinále vedené bodem P 1 . 

□



5.5.5 Průsečnice dvou rovin (základní úloha Z5) 

• Pokud přímka r leží v rovině ρ, pak průsečík 

R přímky r s rovinou σ leží na průsečnici 

p rovin ρ a σ. 

• Průsečnice rovin je přímka ležící v obou 

rovinách, tj. její stopník leží na stopách 

obou rovin. 


Příklad 5.13 Roviny ρ a σ jsou určeny stopami. Sestrojte průsečnici těchto rovin - obr. 5.42. 


1. Nárysný stopník průsečnice leží na nárysné stopě roviny ρ i roviny σ. 

(N 2 ∈ n ρ 2 ∩ n σ 2, N 1 ∈ x 1,2 ). 

2. Půdorysný stopník průsečnice leží na půdorysné stopě roviny ρ i roviny σ. 

(P 1 ∈ p ρ 1 ∩ p σ 1, P 2 ∈ x 1,2 ). 

3. Přímka NP je hledanou průsečnicí. 

Příklad 5.14 Rovina ρ je určena přímkami r a q a rovina σ je dána stopami. Sestrojte průsečnici 

těchto rovin - obr. 5.44. 

□




Řešení: (obr. 5.45) Vyřešíme dvakrát úlohu průsečík přímky s rovinou. 

1. Zvolíme krycí přímku s, tak aby s 2 = q 2 a s ⊂ σ. 

2. Odvodíme půdorys s 2 přímky s. (Úloha 5.5.1). 

3. Najdeme průsečík X 1 přímek s 1 a q 1 . 

4. Odvodíme bod X do nárysu na přímku q. 

5. Podobně zvolíme krycí přímku u a najdeme průsečík Y . 

6. Přímka XY je hledaná průsečnice. 

Poznámka 5.4 Všimněte si, že v některých úlohách jsme ke konstrukcím nepoužívali osu 

x 1,2 , stačilo nám znát směr ordinály. Vzpomeneme si, že kolmé průměty téhož objektu do 

rovnoběžných rovin jsou shodné. Pokud tedy nezáleží na vzdálenosti od průměten, můžeme osu 

x vynechat, případně posunout průměty ve směry ordinály. Je to výhodné zejména v případech, 

kdy se nárys a půdorys překrývají a chceme zobrazení zpřehlednit. 

Není-li zadaná osa x, nemůžeme používat stopy a stopníky. 

□

5.6. Metrické úlohy 42 

5.6 Metrické úlohy 

5.6.1 Skutečná velikost úsečky (základní úloha Z6) 

Na obrázku 5.46 je zřejmé, že body A, B a jejich průměty do půdorysny tvoří lichoběžník 

ABB 1 A 1 s pravými úhly při vrcholech A 1 a B 1 . V tomto lichoběžníku známe, kromě pravých 

úhlů, také velikost strany A 1 B 1 , a velikosti stran AA 1 (z-ová souřadnice bodu A) a BB 1 (zová 

souřadnice bodu B). Tento lichoběžník zobrazíme pomocí sklopení promítací roviny do 

půdorysny. Podobně můžeme provést sklopení do nárysny. 



Příklad 5.15 Sestrojte skutečnou velikost úsečky AB - obr. 5.47. 


1. z A (zetovou souřadnici bodu A) naneseme na kolmici vedenou bodem A 1 , získaný bod 

označíme (A). 

2. z B (zetovou souřadnici bodu B) naneseme na kolmici vedenou bodem B 1 , získaný bod 

označíme (B).


3. Spojnice bodů (A), (B) je sklopená přímka b. Vzdálenost bodů (A), (B) je skutečná 

velikost úsečky AB. 

Poznámka 5.5 Mají-li body A, B opačná znaménka souřadnice z, pak body ABB 1 A 1 netvoří 

lichoběžník, ale čtyřúhelník, ve kterém se dvě strany protínají. Při sklápění tohoto čtyřúhelníku 

naneseme příslušné souřadnice na opačně orientované kolmice. 

Poznámka 5.6 Je-li body A, B je určena přímka p, pak sklopená přímka (p) je určena body 

(A)(B). Odchylka přímky od půdorysny je rovna odchylce přímek p(p). 

Postup pro určování skutečné velikosti úsečky si můžeme zjednodušit použitím metody rozdílového 

trojúhelníka. V obrázku 5.46 je vyznačen pravoúhlý trojúhelník A 1 B 1 (B) ∗ s pravým 

úhlem při vrcholu B 1 . Úsečky (A)(B) a A 1 (B) ∗ jsou rovnoběžné a shodné. Stačí tedy sestrojit 

tento rozdílový trojúhelník, kde velikost strany B 1 (B) ∗ je rovna rozdílu z-ových souřadnic bodů 

A a B. 

I tento postup lze analogicky použít pro nárys, na kolmici k úsečce A 2 B 2 ovšem naneseme 

rozdíl y-ových souřadnic bodů A a B. 

□ 


Příklad 5.16 Sestrojte skutečnou velikost úsečky AB použitím rozdílového trojůhelníka - obr. 

5.49. 

Řešení: (obr. 5.50) Pomocí rozdílového trojúhelníka. 

1. Na kolmici vedenou bodem B 1 naneseme |z A − z B |, získaný bod označíme (B). 

2. Spojnice bodů (B), A 1 je sklopená úsečka AB a vzdálenost bodů (B), A 1 je skutečná 

velikost úsečky AB. 

Je zřejmé, že velikost úsečky rovněž zjistíme, vedeme-li kolmici bodem A (a není přitom důležité, 

do které poloroviny sklápíme). Ve všech případech vyjdou shodné trojúhelníky, které mají 

shodné přepony. Uvedený postup používá místo absolutních souřadnic souřadnice relativní. 

Použití relativních souřadnic vede k možnosti vynechání základnice. 

□


5.6.2 Nanesení úsečky na přímku (základní úloha Z7) 

Sklápění, které jsme využili v úloze 5.6.1, využijeme i v této úloze. Zvolíme na přímce dva body 

a sklopíme ji. Na sklopenou přímku naneseme úsečku ve skutečné velikosti a sklopíme zpět. 

Při sklápění použijeme metodu rozdílového trojúhelníka. 


Příklad 5.17 Je dána přímka b a na ní bod A. Naneste na přímku b od bodu A vzdálenost u 

- obr. 5.51. 


1. Zvolíme na přímce b bod X ≠ A. 

2. Sklopíme úsečku AX (použitím úlohy Z6 z odst. 5.6.1): 

(a) Na kolmici vedenou bodem X 2 naneseme |z X − z A |, získaný bod označíme (X). 

(b) Spojnice bodů (X), A 2 je sklopená přímka b. 

3. Na sklopenou přímku b naneseme velikost u, získaný bod označíme (B). 

4. Bod (B) sklopíme zpět na přímku b 2 pomocí kolmice vedené bodem (B) k přímce b 2 . 

Dostáváme bod B 2 . 

5. Bod B 1 odvodíme po ordinále na přímku b 1 . 

6. Úsečka AB má skutečnou velikost u. 

5.6.3 Přímka kolmá k rovině (základní úloha Z8) 

Při hledání přímky kolmé k rovině je vhodné si přípomenout: 

• Kritérium kolmosti přímky a roviny. 

• Větu o průmětu pravého úhlu. 

□




• Protože h||π, tak k 1 ⊥ h 1 . 

• Protože f||ν, tak k 2 ⊥ f 2 . 

Příklad 5.18 Rovina ρ je určena hlavními přímkami h, f. Sestrojte kolmici k bodem M k rovině 

ρ - obr. 5.54. 


1. Bodem M 1 vedeme kolmici k 1 k přímce h 1 . 

2. Bodem M 2 vedeme kolmici k 2 k přímce f 2 . 

Příklad 5.19 Rovina ρ je určena přímkami p, q. Sestrojte kolmici k bodem M k rovině ρ - 

obr. 5.56. 


□



1. Sestrojíme libovolné hlavní přímky h, f roviny ρ. 

a) Přímka f 1 je rovnoběžná s x 1,2 , f 2 odvodíme pomocí průsečíků přímky f s p a q. 

b) Přímka h 2 je rovnoběžná s x 1,2 , h 1 odvodíme pomocí průsečíků přímky h s p a q. 

2. Postupujeme jako v předchozí úloze. 

a) Bodem M 1 vedeme kolmici k přímce h 1 , dostaneme k 1 . 

b) Bodem M 2 vedeme kolmici k přímce f 2 , dostaneme k 2 . 

5.6.4 Rovina kolmá k přímce (základní úloha Z9) 

Tato úloha je obrácená k úloze předchozí, využijeme opět znalostí kritéria kolmosti přímky 

k rovině a hlavních přímek. Uvědomíme si, že nárys horizontální hlavní hlavní přímky je rovnoběžný 

s osou x 1,2 (neboli kolmý na ordinály) a půdorys je kolmý k zadané přímce. Pro frontální 

hlavní přímku platí, že půdorys je rovnoběžný s osou x 1,2 a nárys je kolmý k zadané přímce. 

Tedy h 1 ⊥ p 1 a h 2 ||x 1,2 a f 2 ⊥ p 2 a f 1 ||x 1,2 . 

Hlavní přímky v této úloze proto neodvozujeme pomocí průsečíků, ale sestrojujeme kolmice 

k průmětům zadané přímky! Je totiž zřejmé, že hlavní přímky jsou zpravidla s danou přímkou 

mimoběžné, a tudíž průsečíky v prostoru neexistují. 

Příklad 5.20 Je dána přímka p. Sestrojíme bodem M rovinu kolmou k přímce p - obr. 5.58. 

Řešení: (obr. 5.59) Sestrojíme hlavní přímky hledané roviny σ. 

1. h 1 ⊥ p 1 a h 2 ||x 1,2 a M 1 ∈ h 1 , M 2 ∈ h 2 . 

2. f 2 ⊥ p 2 a f 1 ||x 1,2 a M 1 ∈ f 1 , M 2 ∈ f 2 . 

3. Rovina σ je určena přímkami h, f. 

□ 

□



5.6.5 Otočení roviny do polohy rovnoběžné s průmětnou (základní 

úloha Z10) 

n 

n 

C 2 

C 

C 1 

r 

p 1 

S 

C 0 

p 

x 

C 

C 1 

C 2 

S 

h 

C 0 

p 

x 

a) b) 


Často je součástí prostorové konstrukce rovinná úloha. Potřebujeme například sestrojit podstavu 

nějakého tělesa v obecné rovině α. Víme, že útvar ležící v rovině rovnoběžné s průmětnou 

se promítne ve skutečné velikosti. Otočíme tedy rovinu α (některé její body) do polohy 

rovnoběžné s průmětnou π (obr. 5.60b)) nebo přímo do průmětny (obr. 5.60a)), provedeme 

požadovanou konstrukci a výsledek otočíme zpět. 

Nejprve musíme určit přímku, kolem které budeme rovinu α otáčet. V případě, že otáčíme 

přímo do průmětny, je osou otáčení průsečnice rovin α a π, tedy stopa roviny α (obr. 5.60a)). 

Nemáme-li zadanou osu x nebo chceme-li si ušetřit práci se sestrojováním stopy, můžeme otočit 

rovinu α do polohy rovnoběžné s průmětnou kolem přímky rovnoběžné s průmětnou, tedy 

hlavní přímky roviny α (obr. 5.60b)). 

Mezi body roviny α a body otočenými do průmětny existuje prostorová geometrická příbuznost 

- osová afinita. Víme, že rovnoběžným průmětem osové afinity získáme osovou afinitu


v rovině, odtud plyne, že při konstrukcích můžeme využívat osové afinity mezi průměty bodů 

(například půdorysy) a otočenými body do téže průmětny (půdorysny). Osou afinity je osa 

otáčení, párem odpovídajících si bodů je průmět bodu (např. A 1 ) a jeho otočený obraz A 0 . 

Postup řešení rovinné úlohy je následující: 

1. Určíme osu otáčení - hlavní přímka nebo stopa roviny. 

2. Sestrojíme rovinu, střed a poloměr kružnice otáčení (příklad 1.1 na straně 8). 

3. Otočíme jeden bod. 

4. Další otočené body získáme pomocí afinity. 

5. Provedeme rovinnou konstrukci. 

6. S využitím afinity otočíme výsledek zpět. 

7. Body výsledného útvaru odvodíme do druhého průmětu. 


Příklad 5.21 Otočme rovinu α kolem stopy do průmětny - obr. 5.61. 

Řešení: (obr. 5.62) Otočíme jeden bod roviny α. 

1. Pomocí horizontální hlavní přímky h roviny α vedené bodem C odvodíme půdorys bodu 

C. 

2. Budeme otáčet do půdorysny, tj. osou otáčení je půdorysná stopa p α 1 . 

3. Rovina otáčení ρ bodu C se promítá do přímky k 1 procházející bodem C 1 a kolmé k ose 

otáčení p α 1 . 

4. Střed otáčení S je průsečík roviny ρ se stopou, tedy S 1 je průsečíkem přímky k 1 se stopou 

p α 1 . 

5. Poloměr otáčení r je skutečná velikost úsečky CS. Skutečnou velikost úsečky určíme sklopením 

- na kolmici k úsečce C 1 S 1 naneseme (relativní) zetovou souřadnici bodu C (tj. 

rozdíl zetových souřadnic bodů C a S, S má zetovou souřadnici 0, protože leží v půdorysně).


C 2 

C 1 

k 1 

S 1 

C 0 

h 2 

h 1 



6. Na kolmici k 1 naneseme od bodu S 1 poloměr r, dostaneme tak otočený bod C 0 . 

Příklad 5.22 Otočme rovinu α, určenou bodem C a hlavní přímkou h, kolem h do roviny 

rovnoběžné s průmětnou - obr. 5.63. 

Řešení: (obr. 5.64) Otočíme jeden bod roviny α. 

1. Otočíme rovinu α kolem hlavní přímky h do polohy rovnoběžné s půdorysnou. 

2. Osou otáčení je hlavní přímka h. 

3. Bodem C 1 vedeme kolmici k 1 k přímce h 1 (rovina otáčení se promítá do k 1 ). 

4. Průsečík přímky k 1 s h 1 je půdorysem středu otáčení S. 

5. Sklopíme úsečku CS a zjistíme skutečnou velikost poloměru otáčení r (na kolmici k C 1 S 1 

naneseme rozdíl zetových souřadnic bodu CS a přímky h). 

6. Od bodu S 1 naneseme na k 1 poloměr r a získáme otočený bod C 0 . 

Příklad 5.23 V rovině ρ jsou dány body A a C svými nárysy. Sestrojíme čtverec ABCD 

s úhlopříčkou AC ležící v rovině ρ - obr. 5.65. 

Řešení: (obr. 5.66) Sestrojení čtverce je rovinná úloha. Rovinu ρ otočíme do půdorysny, sestrojíme 

čtverec v otočení a výsledek otočíme zpět. 

1. Pomocí hlavní přímky odvodíme bod C do půdorysu, půdorys bodu A leží na ose x 1,2 . 

2. Otočíme bod C do půdorysny - získáme bod C 0 . 

3. Bod A 0 sestrojíme pomocí afinity (osa afinity je p ρ 1, pár odpovídajících si bodů je A 1 , A 0 . 

4. V otočení sestrojíme čtverec A 0 B 0 C 0 D 0 . 

5. Pomocí afinity otočíme čtverec zpět do půdorysu. (Můžeme využít rovnoběžnosti protějších 

stran.) 

6. S využitím hlavních přímek najdeme nárys čtverce. 

□ 

□ 

□



5.6.6 Obraz kružnice (základní úloha Z11) 

Podívejme se, jak se v pravoúhlém promítání zobrazí kružnice. Pokud kružnice leží v rovině 

rovnoběžné s průmětnou, bude jejím obrazem shodná kružnice. Obrazem kružnice ležící v rovině 

kolmé na průmětnu bude úsečka, jejíž délka je rovna průměru kružnice. Obrazem kružnice 

v obecném případě je elipsa. Velikost průměru kružnice, který leží na hlavní přímce, se při 

pravoúhlém promítání zachová, ostatní průměry se v pravoúhlém promítání zkracují. Průměr 

na hlavní přímce bude tedy hlavní osou elipsy, do které se kružnice zobrazí. 

Obrázek 5.67: Obrázek 5.68:


Příklad 5.24 V rovině ρ(h, f) sestrojme kružnici k(S, r) - obr. 5.67. 


1. Na horizontální hlavní přímku h naneseme v půdorysu od bodu S 1 na obě strany skutečnou 

velikost poloměru r - body označíme A 1 , B 1 a odvodíme je po ordinále do nárysu. 

2. Na frontální hlavní přímku f naneseme v nárysu od bodu S 2 na obě strany skutečnou 

velikost poloměru r - body označíme C 2 , D 2 a odvodíme je po ordinále do půdorysu. 

3. Obrazem kružnice v půdorysu je elipsa s hlavní osou A 1 B 1 , body C 1 , D 1 leží na elipse. 

Pomocí proužkové konstrukce získáme vedlejší osu. 

4. Obrazem kružnice v nárysu je elipsa s hlavní osou C 2 D 2 , body A 2 , B 2 leží na elipse. 

Pomocí proužkové konstrukce získáme vedlejší osu. 

5.6.7 Transformace průměten (základní úloha Z12) 

V předchozích úlohách jsme již mluvili o možnosti vynechání osy x, to znamená o posunutí 

půdorysny nebo nárysny. Nárys nebo půdorys útvarů se neměnil, neboť poloha nových průměten 

byla rovnoběžná s původními. 

Nyní přejdeme od původních průměten k nové dvojici navzájem kolmých průměten. Jednu 

průmětnu necháme v původní poloze a jako druhou volíme libovolnou rovinu k ní kolmou 

(volíme ji vhodně tak, aby se použitím nových průměten úloha zjednodušila). 

Zvolíme například třetí průmětnu µ kolmou k půdorysně π – obr. 5.69. Průsečnice rovin 

µ a π bude novou osou x - označíme ji x 1,3 . Promítneme bod M do třetí průmětny, průmět 

označíme indexem M 3 a provedeme sdružení průmětů. Ordinála bude spojnicí bodů M 1 a M 3 

a bude kolmá k ose x 1,3 , vzdálenost M 3 od osy x 1,3 je z-ovou souřadnicí bodu M - obr. 5.70. 

□ 


Příklad 5.25 Určeme vzdálenost bodu A od roviny ρ s využitím třetí průmětny (obr. 5.71). 

Řešení: (obr. 5.72)



1. Zvolíme třetí průmětnu µ kolmou k půdorysně a kolmou k rovině ρ - rovina ρ se do nové 

průmětny zobrazí jako přímka. 

2. Najdeme třetí průmět bodu A. 

3. Najdeme třetí průmět libovolného bodu roviny ρ - zvolili jsme stopník N. 

4. Třetím průmětem roviny ρ je přímka procházející bodem N 3 a protínající se se stopou p ρ 1 

na ose x 1,3 . 

5. Vzdálenost A 3 a ρ 3 je hledanou vzdáleností bodu A od roviny ρ. 

□ 


5.1 Definujte pojem stopník a stopa. 

5.2 Vysvětlete pojem hlavní přímka. 

5.3 Vysvětlete metodu krycí přímky. 

5.4 K čemu se používá otáčení roviny? 

5.5 V čem se liší otáčení roviny okolo stopy a okolo hlavní přímky?

Kapitola 6 

Axonometrie 

6.1 Úvod 

Předpokládejme, že je v prostoru dána kartézská soustava souřadnic. Souřadnicové roviny nazýváme 

půdorysna - xy ( 1 π), nárysna xz ( 2 π) a bokorysna yz ( 3 π). V praxi obvykle umísťujeme 

objekty co nejvýhodněji vzhledem k osám. Např. hranol nebo válec umístíme tak, aby měl podstavu 

v souřadnicové rovině. Útvar, který má osu, umístíme tak, aby jeho osa byla rovnoběžná s 

osou soustavy souřadnic. Jestliže promítneme pravoúhle tento objekt do souřadnicových rovin 

(Mongeova projekce), budou se nám snadno řešit polohové a metrické úlohy, ale chybí názorný 

pohled. Názornou zobrazovací metodou, která využívá výhody rovnoběžného promítání, 

je axonometrie. 

Obrázek 6.1: 

Axonometrie je rovnoběžné promítání na jednu průmětnu α takové, že směr promítání s 

není rovnoběžný s žádnou souřadnicovou rovinou, tj. osy se promítají do tří různých přímek 

x A , y A , z A - obr.6.1. 

Rovinu α nazýváme axonometrickou průmětnou; x A , y A , z A axonometrickými průměty 

os x, y, z; B A axonometrickým průmětem bodu B. Pravoúhlé průměty bodu B 

do souřadnicových rovin jsou půdorys (xy), nárys (xz) a bokorys (yz) a jejich průměty do 

53

6.2. Klasifikace axonometrií 54 

axonometrické průmětny axonometrický půdorys (B 1A ), nárys (B 2A ) a bokorys (B 3A ). 

Jednotky na osách (j x , j y , j z ) se promítnou do axonometrických jednotek (j xA , j yA , j zA ). 

Chceme-li zadat axonometrii, vycházíme z následující věty: 

Věta 6.1 (Pohlkeova věta) Tři úsečky se společným koncovým bodem, které leží v jedné rovině 

a neleží na jedné přímce, můžeme považovat za rovnoběžný průmět tří navzájem kolmých a 

shodných úseček v prostoru. 

6.2 Klasifikace axonometrií 

Podle velikosti axonometrických jednotek j x , j y , j z : 

1. izometrie ( j x = j y = j z ) - obr. 6.2a) 

2. dimetrie ( j x = j y nebo j y = j z nebo j x = j z ) - obr. 6.2b) 

3. trimetrie ( j x ≠ j y ≠ j z ) - obr. 6.2c) 

z 

z 

z 

j x 

j x 

y 

j y 

Obrázek 6.2: 

j y 

y 

x 

j x 

x 

x 

a) b) c) 

y 

Podle směru promítání 

1. Směr s je kolmý k axonometrické průmětně, axonometrie se nazývá pravoúhlá. 

2. Směr s není kolmý k axonometrické průmětně, axonometrie se nazývá obecná nebo také 

kosoúhlá. 

Uveďme si ještě některé speciální axonometrie: 

1. Kosoúhlé promítání. Průmětnou je souřadnicová rovina yz a směr není kolmý k průmětně. 

Na osách y a z jsou jednotky stejné, na ose x se jednotka obvykle zkracuje. Je to 

dimetrie nebo izometrie. 

2. Vojenská perspektiva. Průmětnou je souřadnicová rovina xy a směr není kolmý k 

průmětně. Na všech osách je stejné zkrácení jednotek. Promítání je izometrie.

6.3. Zobrazení bodu 55 

3. Pravoúhlá axonometrie. Průmětnou je obecná rovina, která protíná osy v bodech 

různých od počátku. Směr je kolmý k průmětně. Pravoúhlou axonometrií se budeme ještě 

podrobněji zabývat, protože má některé pěkné vlastnosti. 

6.3 Zobrazení bodu 

Jedním průmětem není bod v prostoru jednoznačně určen, proto musíme k axonometrickému 

průmětu zadávat ještě některý z pravoúhlých průmětů do souřadnicových rovin. Obvyklé je 

zadání dvojicí B A a B 1A . Bod však může být určen libovolnou dvojicí z bodů B A , B 1A , B 2A , 

B 3A (např. B 1A , B 3A ). 

Na obrázku 6.3 je axonometrický obraz 

bodu B[2, 3, 4], jeho axonometrický nárys, 

půdorys a bokorys. 

Obrázek 6.3: 

Poznámka 6.1 Pro zjednodušení budeme 

tam, kde nemůže dojít k záměně, axonometrické 

průměty označovat bez dolního indexu 

A a vynechávat přívlastek axonometrický. 


Příklad 6.1 Bod je v axonometrii určen dvojicí A a A 3 - obr. 6.4. Doplníme zbývající pravoúhlé 

průměty do souřadnicových rovin. 

Řešení: (obr.6.5) Pomocí rovnoběžek s osami x, y, z doplníme zbývající průměty. 

□

6.4. Zobrazení přímky 56 


Příklad 6.2 Zobrazíme body A ∈ xy, B ∈ yz, C ∈ xz - obr. 6.6. 

Řešení: (obr.6.7) 

A ∈ xy ⇒ A = A 1 , A 2 ∈ x, A 3 ∈ y 

B ∈ yz ⇒ B = B 3 , B 2 ∈ z, B 1 ∈ y 

C ∈ xz ⇒ C = C 2 , C 1 ∈ x, C 3 ∈ z 

□ 

6.4 Zobrazení přímky 

Přímka je určena dvěma body, průmět přímky je tedy určen průměty dvou bodů. 

Obrazem přímky p, která není kolmá k průmětně, je opět přímka. Zadáváme ji opět pomocí 

axonometrického průmětu p A a pravoúhlého průmětu do souřadnicové roviny (např. p 1A ). 

Stopník je opět průsečík přímky s průmětnou, ovšem v tomto případě s průmětnou axonometrickou. 

Tento stopník ale v konstrukcích zpravidla nevyužíváme. Výhodné jsou pro nás 

pomocné stopníky, jimiž jsou průsečíky přímky se souřadnicovými rovinami (xy, xz, yz). Nazýváme 

je půdorysný, nárysný a bokorysný stopník. 

Příklad 6.3 Sestrojíme půdorysný, nárysný a bokorysný stopník přímky a - obr. 6.8. 


Průsečík přímky a a jejího půdorysu a 1 je půdorysný stopník P = P 1 . 

Průsečík přímky a 1 s osou x je půdorys nárysného stopníku N 1 , nárysný stopník N najdeme 

na přímce a a na rovnoběžce s osou z vedené bodem N 1 . 

Průsečík přímky a 1 s osou y je půdorys bokorysného stopníku M 1 , bokorysný stopník M 

najdeme na přímce a a na rovnoběžce s osou z vedené bodem M 1 . 

□

6.5. Zobrazení roviny 57 


6.5 Zobrazení roviny 

Rovinu můžeme určit pomocí průmětů prvků, které ji určují (např. třemi různými nekolineárními 

body, dvěma rovnoběžkami, dvěma různoběžkami nebo přímkou a bodem, který na ní 

neleží). Nejnázornější je zadání roviny pomocí stop. Stopa roviny je průsečnice roviny s průmětnou, 

ale my budeme (stejně jako u stopníků) používat průsečnice roviny se souřadnicovými 

rovinami (xy, xz, yz). Nazýváme je půdorysná, nárysná a bokorysná stopa. 


Každá dvojice stop se protíná na ose (průsečík může být i nevlastní bod, tj. stopy jsou pak 

rovnoběžné). Pro určení roviny stačí zadat dvě stopy, jsou to dvě různoběžné nebo rovnoběžné 

přímky. Třetí stopu snadno doplníme pomocí průsečíků s osami - obr. 6.10 nebo 6.11. 

Na obrázku 6.12 jsou stopy roviny ρ rovnoběžné s půdorysnou xy, stopy roviny σ rovnoběžné 

s bokorysnou yz a stopy roviny τ rovnoběžné s nárysnou yz. Na obrázku 6.13 jsou stopy roviny 

α kolmé na nárysnu xz, stopy roviny β kolmé na půdorysnu xy a stopy roviny γ kolmé na 

bokorysnu yz.

6.6. Úlohy v axonometrii 58 


6.6 Úlohy v axonometrii 

V obecné axonometrii se zaměříme pouze na polohové úlohy a ukážeme si, jak lze zobrazit 

kružnici. Další typy úloh jsou nejen příliš složité, ale zejména jejich řešení umožňuje Mongeova 

projekce. Pomocí přepočtu délek na osách pak může být zobrazen v axonometrii jen výsledek. 


6.6.1 Vzájemná poloha přímek 

Z axonometrických průmětů přímek a jejich půdorysů můžeme určit jejich vzájemnou polohu. 

Z vlastností rovnoběžného promítání plyne, že rovnoběžné přímky se budou promítat jako 

rovnoběžky (pokud se nepromítnou jako dva body). Rovnoběžné budou jak jejich axonometrické 

průměty, tak jejich půdorysy - obr. 6.14a). Na obrázku 6.14b) jsou různoběžky, průsečík jejich 

axonometrických průmětů a půdorysů leží na rovnoběžce s osou z (můžeme ji říkat ordinála) 

na rozdíl od mimoběžek - obr. 6.14c).


6.6.2 Přímka v rovině 

Připomeňme důležité vlastnosti: 

• Přímka ležící v rovině je se všemi ostatními přímkami rovnoběžná nebo různoběžná. 

• Přímka leží v rovině, právě když všechny stopníky přímky leží na příslušných stopách 

roviny. 

Těchto vlastností využijeme i v následujících úlohách. 


Příklad 6.4 Je dána rovina ρ. Sestrojme axonometrický průmět přímky m ∈ ρ, je-li dán její 

půdorys m 1 - obr. 6.15. 


1. Najdeme průsečík přímky m 1 s půdorysnou stopou p ρ 1 roviny ρ, získali jsme půdorysný 

stopník P = P 1 . 

2. Průsečík přímky m 1 s osou y je půdorys bokorysného stopníku M 1 . 

3. Bokorysný stopník M najdeme na bokorysné stopě m ρ a na rovnoběžce s osou z vedené 

bodem M 1 . (Podobně bychom mohli sestrojit i nárysný stopník, ale pro konstrukci přímky 

stačí kterékoliv dva ze tří stopníků.) 

4. Oba stopníky leží na přímce m, axonometrický průmět přímky m je proto jejich spojnicí. 

(Nárysný stopník by ležel na také na přímce m.) 

Příklad 6.5 Je dána rovina ρ(a, b). Sestrojte m 1 , je-li dán axonometrický průmět přímky m ∈ 

ρ - obr. 6.17. 


1. Najdeme průsečíky A, B přímky m s přímkami a, b. 

2. Body A, B odvodíme na přímky a 1 a b 1 a získáme jejich půdorysy A 1 a B 1 . 

3. Přímka m 1 prochází body A 1 a B 1 . 

□ 

□



6.6.3 Průsečík přímky s rovinou 

Průsečík přímky k s rovinou ρ budeme opět hledat metodou krycí přímky. Podobně jako v 

Mongeově projekci volíme krycí přímku s tak, aby krycí přímka ležela v rovině ρ. Máme dvě 

možnosti volby této krycí přímky: buď se kryjí axonometrické průměty přímek k a s a hledáme 

průsečík jejich půdorysů nebo se kryjí půdorysy a hledáme průsečík axonometrických průmětů 

přímek k a s. V následujících dvou příkladech jsme volili první možnost. 


Příklad 6.6 Sestrojíme průsečík přímky k s rovinou ρ, určenou stopami - obr. 6.19. 


1. Volíme krycí přímku s tak, že axonometrické průměty přímek s a k splynou a s ⊂ ρ. 

2. Odvodíme půdorys přímky s pomocí stopníků N a M. Půdorys přímky s označíme s 1 . 

3. Průsečík přímek s 1 a k 1 je půdorysem hledaného průsečíku P 1 . Axonometrický průmět 

bodu P odvodíme pomocí ordinály (rovnoběžky s osou z).



Příklad 6.7 Sestrojíme průsečík přímky k s rovinou ρ, určenou stopami - obr. 6.21. 


1. Volíme krycí přímku s tak, že axonometrické průměty přímek s a k splynou a s ⊂ ρ. 

2. Odvodíme půdorys přímky s pomocí průsečíků A, B s přímkami a a b. Půdorys přímky 

s označíme s 1 . 

3. Průsečík přímek s 1 a k 1 je půdorysem hledaného průsečíku P 1 . Axonometrický průmět 

bodu P odvodíme pomocí ordinály (rovnoběžky s osou z). 

6.6.4 Průsečnice rovin 

Jsou dány roviny ρ a σ. Pokud je alespoň jedna z rovin, např. ρ, určena obecně zadanými 

přímkami, najdeme dvakrát průsečík přímky s rovinou σ a jejich spojnice je průsečnicí zadaných 

rovin. 

Jednodušší situaci máme, jestliže jsou obě roviny zadané stopami. Poznamenejme, že stopy 

roviny umíme najít pomocí stopníků. Půdorysné stopy obou rovin leží v rovině xy. Jejich 

průsečík je půdorysný stopník hledané průsečnice. Podobně můžeme najít nárysný stopník 

jako průsečík nárysných stop a bokorysný stopník jako průsečík bokorysných stop. Pro určení 

průsečnice stačí nalézt dva z těchto stopníků. 

Příklad 6.8 Sestrojíme průsečnici rovin ρ a σ, určených stopami - obr. 6.23. 


1. Průsečík nárysných stop n ρ a n σ je nárysný stopník N hledané průsečnice. Jeho půdorys 

N 1 leží na ose x. 

□ 

□



2. Průsečík bokorysných stop m ρ a m σ je bokorysný stopník M hledané průsečnice. Jeho 

půdorys M 1 leží na ose y. 

3. Spojnice bodů N a M je průsečnice rovin ρ a σ. 

4. Půdorysný stopník P je průsečíkem půdorysných stop a také leží na sestrojené průsečnici. 

6.6.5 Kružnice v souřadnicové rovině 

Obrazem kružnice v axonometrii je elipsa, protože se jedná o rovnoběžné promítání. Průměry 

kružnice, které jsou rovnoběžné s osami ležícími v rovině kružnice se zobrazí do sdružených 

průměrů elipsy. Hlavní osy elipsy získáme pomocí Rytzovy konstrukce. 

□ 


Příklad 6.9 Sestrojíme kružnici se středem v bodě S a poloměrem 3 jednotky ležící v rovině 

yz - obr. 6.25.

6.7. Pravoúhlá axonometrie 63 


1. Bodem S vedeme rovnoběžku s osou y a naneseme na ni na obě strany třikrát jednotku 

j y . Získané body označíme A, B. 

2. Bodem S vedeme rovnoběžku s osou z a naneseme na ni na obě strany třikrát jednotku 

j z . Získané body označíme C, D. 

3. Úsečky AB a CD jsou sdružené průměry elipsy, do které se zobrazí kružnice v rovině yz. 

4. Hlavní osy sestrojíme pomocí Rytzovy konstrukce. 

□ 

6.7 Pravoúhlá axonometrie 

Půdorysnu, nárysnu a bokorysnu protneme rovinou α, která neprochází počátkem a protíná 

všechny tři osy - obr. 6.27. Průsečíky roviny α s osami označíme X, Y, Z. Trojúhelník XY Z je 

vždy ostroúhlý. Rovina α je axonometrickou průmětnou, do které budeme pravoúhle promítat. 

Trojúhelníku XY Z říkáme axonometrický trojúhelník. Tento trojúhelník se zobrazoje 

vždy ve skutečné velikosti, neboť leží v axonometrické průmětně. 


Podívejme se, jak se zobrazí v pravoúhlé axonometrii osy x, y, z. Osa z je kolmá k rovině 

xy, a tudíž ke všem přímkám této roviny, tedy i k přímce XY . Přímka XY leží v axonometrické 

průmětně. Podle věty 4.1 o pravoúhlém průmětu pravého úhlu se osa z a přímka XY zobrazí 

jako kolmice. Stejné závěry můžeme udělat i o ose y a přímce XZ a ose x a přímce Y Z. Můžeme 

proto vyslovit následující větu: 

Věta 6.2 Osy x, y, z se promítnou do výšek axonometrického trojúhelníka - obr. 6.28. 

Je-li dán axonometrický trojúhelník, umíme sestrojit axonometrické průměty os. Obráceně: 

jsou-li dány průměty os (axonometrický osový kříž), můžeme sestrojit nekonečně mnoho axonometrických 

trojúhelníků, které jsou navzájem podobné. Volbou axonometrického trojúhelníka


volíme axonometrickou průmětnu dál nebo blíž od počátku. Volba axonometrického trojúhelníka, 

a tím i axonometrické průmětny, nemá vliv na velikost a tvar průmětů, protože všechny 

tyto roviny jsou navzájem rovnoběžné. 

Pravoúhlá axonometrie je speciálním případem axonometrie obecné, proto řešíme polohové 

úlohy stejně jako v obecné axonometrii. Navíc si ukážeme řešení rovinných úloh v půdorysně, 

nárysně a bokorysně. 

6.7.1 Metrické úlohy v rovinách xy, yz, zx 

Rovinné úlohy v rovinách xy, yz a zx řešíme pomocí otočení příslušné roviny do axonometrické 

průmětny. Osou otáčení je jedna z přímek XY , Y Z, ZX. Do axonometrické průmětny vždy 

nejprve otočíme počátek. Mezi axonometrickými průměty bodů a jejich otočenými průměty 

opět existuje afinita, další body tedy získáme pomocí afinity. V otočení vyřešíme rovinnou úlohu 

(najdeme velikosti jednotek na osách, sestrojíme podstavu tělesa atd.) a výsledek otočíme zpět 

do axonometrické průmětny. 

Pro určení obecné axonometrie jsme museli zadat axonometrický osový kříž s velikostmi 

jednotek na jednotlivých osách. Tím byla obecná axonometrie podle Pohlkeovy věty 6.1 jednoznačně 

určena. V pravoúhlé axonometrii máme zadán směr promítání a umíme určit jednotky 

na osách,což si ukážeme v následujícím příkladu. 


Příklad 6.10 Je dán axonometrický trojúhelník XY Z. Sestrojíme průměty os x, y, z a jednotky 

na osách - obr. 6.29. 


1. Osy x, y, z se promítnou do výšek axonometrického trojúhelníka XY Z. 

2. Otočíme rovinu xy kolem přímky XY . Otáčíme bod O: rovina otáčení je kolmá k přímce 

XY a prochází bodem O, promítne se do přímky k. Nemusíme hledat střed a poloměr 

otáčení, protože víme, že přímky x a y jsou ve skutečnosti kolmé a musí po otočení přejít 

do kolmic. Otočený bod O leží na přímce k a na Thaletově kružnici sestrojené nad úsečkou 

XY , označíme ho (O).


3. Otočená přímka x (označíme ji (x)) prochází bodem (O) a bodem X, který při otáčení 

zůstává na místě, protože leží na ose otáčení. 

4. Otočená přímka y (označíme ji (y)) prochází bodem (O) a bodem Y , který při otáčení 

zůstává na místě, protože leží na ose otáčení. 

5. Na otočených osách vyznačíme jednotky ve skutečné velikosti. 

6. Pomocí afinity s osou XY a párem odpovídajících si bodů O, (O) odvodíme jednotky na 

osy x a y. 

7. Pomocí otočení roviny yz kolem přímky Y Z získáme stejným způsobem jednotky na ose 

z (a znovu na ose y). 

8. Není třeba otáčet rovinu xz, protože bychom jen znovu získali jednotky na osách x a z. 

□ 


Příklad 6.11 V pravoúhlé axonometrii určené osovým křížem sestrojíme obraz čtverce ABCD, 

který leží v rovině yz, je-li dána úhlopříčka AC. - obr. 6.31. 


1. Sestrojíme axonometrický trojúhelník XY Z. Strany trojúhelníka jsou kolmé na osy x, y a 

z. Stranu Y Z volíme tak, aby procházela bodem A (zjednodušíme si tím další konstrukci). 

2. Pomocí Thaletovy kružnice a kolmice bodem O k přímce Y Z otočíme bod O - otočený 

bod označíme O 0 . 

3. S použitím afinity s osou Y Z a párem odpovídajících si bodů O, O 0 otočíme body A a 

C (bod A je samodružný, protože jsme přímku Y Z, neboli osu otáčení, zvolili bodem A. 

Otočené body označíme A 0 a C 0 . 

4. V otočení sestrojíme čtverec A 0 B 0 C 0 D 0 . 

5. Pomocí afinity otočíme čtverec zpět a získáme axonometrický obraz čtverce ABCD ležícího 

v rovině yz 

Podobně můžeme sestrojovat rovinné útvary v rovinách xy a xz. 

□


6.7.2 Obraz kružnice ležící v některé souřadnicové rovině 

Kružnici v půdorysně, nárysně nebo bokorysně můžeme sestrojit stejně jako v příkladu 6.9. 

V pravoúhlé axonometrii si však můžeme tuto úlohu zjednodušit. V pravoúhlém promítání se 

úsečky rovnoběžné s průmětnou zobrazí ve skutečné velikosti a všechny ostatní se promítnutím 

zkrátí. To znamená, že velikosti stran axonometrického trojúhelníka a všech úseček s nimi 

rovnoběžných se zobrazí ve skutečné velikosti. Průměr kružnice k ležící v rovině xy rovnoběžný 

s úsečkou XY se promítne do hlavní osy elipsy, do které se zobrazí kružnice k. Podobně hlavní 

osa elipsy, do které se zobrazí kružnice ležící v rovině yz, je rovnoběžná s úsečkou Y Z a rovna 

skutečnému poloměru kružnice. Hlavní osa elipsy, do které se zobrazí kružnice ležící v rovině 

zx, je rovnoběžná s úsečkou ZX a rovna skutečnému poloměru kružnice. 

Protože pravoúhlé promítání zachovává rovnoběžnost, můžeme najít další bod kružnice na 

rovnoběžkách vedenými hlavními vrcholy elipsy s osami ležícími v rovině kružnice. 


Příklad 6.12 V pravoúhlé axonometrii určené axonometrickým trojúhelníkem sestrojte kružnici 

m(V ; r 1 ) ležící v rovině xy a kružnici n(U; r 2 ) ležící v rovině yz - obr. 6.33. 


1. Sestrojíme osy x, y, z jako výšky axonometrického trojúhelníka XY Z. 

2. Bodem V vedeme rovnoběžku s přímkou XY a naneseme na ni na obě strany velikost r 1 . 

Body označíme A a B, jsou to hlavní vrcholy elipsy m. 

3. Bodem A vedeme rovnoběžku s osou x a bodem B rovnoběžku s osou y, jejich průsečík 

je bod M. Bod M je bodem elipsy. Nyní můžeme pomocí proužkové konstrukce (není v 

obrázku vyznačena) sestrojit vedlejší osu hledané elipsy a tedy i celou elipsu m. 

4. Elipsa m je obrazem hledané kružnice m(V ; r 1 ). 

5. Podobně sestrojíme obraz kružnice n(U; r 2 ) v rovině yz: hlavní osa CD elipsy je rovnoběžná 

s přímkou Y Z a její velikost je rovna poloměru r 2 . Bod N je průsečíkem rovnoběžek 

vedených body C a D s osami z a y. K sestrojení elipsy použijeme opět proužkovou konstrukci.


Stejně bychom setrojili i kružnici v rovině xz a kružnice v rovinách rovnoběžných s rovinami 

xy, yz a xz. 

□ 

Nyní umíme sestrojit rovinný útvar v půdorysně, nárysně a bokorysně. To znamená, že 

umíme sestrojit základní tělesa jako hranoly, válce, kužele a jehlany s podstavou v těchto 

rovinách. V další kapitole se ještě naučíme řešit průniky těchto těles s přímkami a rovinami. 


6.1 Uveďte, čím je obecně určena axonometrie. 

6.2 Uveďte dva základní způsoby určení pravoúhlé axonometrie a popište vzájemný vztah 

mezi určujícími prvky v prvním a druhém způsobu určení. 

6.3 Jakou konstrukci elipsy využijete při zobrazení kružnice v pravoúhlé, resp. obecné axonometrii?

Literatura 

[1] Bohne, E. – Klix, W.D.: Geometrie – Grundlagen für Anwendungen. Leipzig, Fachbuchverlag 

1995. 

[2] Polák, J.: Přehled středoškolské matematiky. Praha, SPN 1991. 

[3] Rogers, D.F. – Adams, J.A.: Mathematical Elements for Computer Graphics. New York, 

Mc Graw–Hill 1990. 

[4] Štauberová, Z.: Mongeovo promítání. Plzeň, ZČU 2004. 1997. 

[5] Urban, A.: Deskriptivní geometrie I. Praha, SNTL 1965. 

68

DeskriptivnÃ­ geometrie 1

Create successful ePaper yourself

Delete template?

Save as template?

DeskriptivnÃ geometrie 1