CEBťRSEL TOPOLOJť ARA SINAV CEVAP ANAHTARI 1. R Çözüm: R

22.11.2011
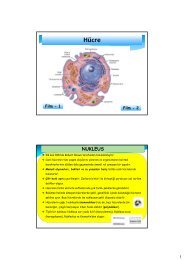
CEB RSEL TOPOLOJ
ARA SINAV CEVAP ANAHTARI
1. R 2 nin herhangi bir kapal alt kümesi D 2 diskinin içine homeomorf mudur Cevabnz açklaynz.
Çözüm: R 2 bir Hausdor uzay oldu§undan kapal her alt kümesi kompakttr. Fakat D 2 diskinin içi
kompakt olmad§ndan bu iki uzay birbirine homeomorf de§ildir.
2. (X, τ) bir topolojik uzay ve Y bo³tan farkl bir küme olmak üzere f : X → Y örten bir fonksiyon
olsun. f fonksiyonunu sürekli klan Y üzerindeki en ince topolojinin identikasyon topolojisi oldu§unu
ispatlaynz.
Çözüm: τ q , Y üzerindeki identikasyon topolojisi ve τ ′ , Y üzerinde τ q ⊆ τ ′ ve f fonksiyonunu sürekli
klacak ³ekilde bir topoloji olsun. Y üzerinde τ q identikasyon topolojisini göz önüne ald§mzda, identi-
kasyon topolojisinin tanm gere§i her U ∈ τ q için f −1 (U) ∈ τ oldu§undan f : X → Y süreklidir. Key
bir V ∈ τ ′ alalm. f : (X, τ) → (Y, τ ′ ) sürekli oldu§undan f −1 (V ) ∈ τ olur ve τ q tanm gere§i V ∈ τ q
elde edilir. O halde τ ′ ⊆ τ q .
3. ∼, bir X topolojik uzay üzerinde bir denklik ba§nts ve R = {(x, y) ∈ X × X : x ∼ y} olsun.
q : X → X/ ∼ bir do§al dönü³üm olsun. R ⊂ X × X açk ise, i x (y) = (x, y) ile tanml i x : X → {x} × X
homeomorzm olmak üzere X/ ∼ üzerindeki bölüm topolojisinin diskret oldu§unu gösteriniz.
Çözüm: X/ ∼ üzerindeki topolojinin diskret olabilmesi için her denklik snfnn açk oldu§unu göstermeliyiz.
R ⊂ X × X açk oldu§undan bir x 0 ∈ X için
({x 0 } × X) ∩ R = {(x 0 , y) ∈ {x 0 } × X : x 0 ∼ y} ⊂ {x 0 } × X
açktr. i x0 : X → {x 0 } × X homeomorzma oldu§undan
i −1
x 0
(({x 0 } × X) ∩ R) = i −1
x 0
({(x 0 , y) ∈ {x 0 } × X : x 0 ∼ y})
açktr.
= {y ∈ X : x 0 ∼ y}
= [x 0 ]
4. Bir Hausdor uzaynn retraksiyonunun kapal oldu§unu gösteriniz.
Çözüm: X bir Hausdor uzay, A ⊂ X ve r : X → A bir retraksiyon olsun. Bu durumda A = {x ∈
X : x = r(x)}. x ∈ X − A olsun, o zaman x ≠ r(x). X bir Hausdor uzay oldu§undan x ∈ U ve r(x) ∈ V
olacak ³ekilde ayrk ve açk U, V kümeleri vardr. V ∩ A, A da açktr. Böylece r −1 (V ∩ A), X te açktr.
x ∈ U, x ∈ r −1 (V ∩ A) ve iki açk kümenin arakesiti de açk oldu§undan G = U ∩ r −1 (V ∩ A) açktr ve

x noktasn içerir. Ayrca G ∩ A = ∅ oldu§undan X − A açktr. O halde A kapaldr.
5. (1, 0), (3, 5) ∈ R 2 olmak üzere π 1 (R 2 , (1, 0)) temel grubunu hesaplaynz. π 1 (R 2 , (1, 0)) ile π 1 (R 2 , (3, 5))
temel gruplar izomorf mudur Açklaynz.
Çözüm:
Teorem: α, X uzaynda x 0 noktasndan x 1 noktasna bir yol olsun. Bu durumda ̂α([f]) = [α] ∗ [f] ∗ [α]
ile tanml ̂α : π 1 (X, x 0 ) → π 1 (X, x 1 ) homomorzmas bir izomorzmdir.
Sonuç: X yol ba§lantl bir uzay ise, her x 0 , x 1 ∈ X için π 1 (X, x 0 ) ∼ = π 1 (X, x 1 )
Bu soruda da R 2 yol ba§lantl oldu§undan büzülebilirdir ve π 1 (R 2 , (1, 0)) ∼ = {0} ∼ = π 1 (R 2 , (3, 5)).
6. f, f ′ : X −→ Y ve g, g ′ : Y −→ Z homotopik ise g ◦ f, g ′ ◦ f ′ 'ye homotop oldu§unu gösteriniz.
Çözüm: f ≃ f ′ oldu§undan F : X × I −→ Y sürekli dönü³ümü F (x, 0) = f(x), F (x, 1) = f ′ (x)
ko³ullarn sa§lar. g ≃ g ′ oldu§undan G : Y × I −→ Z sürekli dönü³ümü G(x, 0) = g(x), G(x, 1) = g ′ (x)
ko³ullarn sa§lar. g ◦ f ≃ g ′ ◦ f ′ oldu§unu göstermek için ≃ ba§ntsnn denklik ba§nts oldu§undan
yararlanaca§z. g◦f ≃ g◦f ′ ve g◦f ′ ≃ g ′ ◦f ′ oldu§unu gösterirsek g◦f ≃ g ′ ◦f ′ oldu§unu göstermi³ oluruz.
• X × I F Y
g
Z
H : X × I −→ Z, H(x, t) = g ◦ F (x, t) ³eklinde tanmlanan dönü³üm F ve g sürekli oldu§undan
süreklidir. H(x, 0) = g◦F (x, 0) = g◦f(x) ve H(x, 1) = g◦F (x, 1) = g◦f ′ (x) oldu§undan g◦f ≃ g◦f ′
dir.
• X × I f ′ ×1 Y × I G Z
G◦(f ′ ×1) : X ×I −→ Z sürekli dönü³ümü G◦(f ′ ×1)(x, 0) = g◦f ′ (x) ve G◦(f ′ ×1)(x, 1) = g ′ ◦f ′ (x)
ko³ullarn da sa§lad§ndan g ◦ f ′ ≃ g ′ ◦ f ′ dir.
O halde g ◦ f ≃ g ′ ◦ f ′ dir.
7. Bir X uzaynn büzülebilir olmas için gerek ve yeter bir ³art Y herhangi bir topolojik uzay olmak
üzere her f : Y → X dönü³ümünün nullhomotop olmasdr. spatlaynz.
Çözüm: X uzaynn büzülebilir oldu§unu kabul edelim. Bu durumda id X ≃ c x0 olacak ³ekilde bir
H : X × I → X homotopi dönü³ümü vardr. f : Y → X herhangi bir sürekli dönü³üm olsun ve her
(y, t) ∈ Y × I için G(y, t) = H ◦ (f × id I )(y, t) = H(f(y), t) ile tanml dönü³ümü göz önüne alalm.
• H, f ve id I dönü³ümleri sürekli oldu§undan G süreklidir.
• G(y, 0) = H(f(y), 0) = f(y) ve G(y, 1) = H(f(y), 1) = c x0 (f(y)) = x 0
oldu§undan f = id X ◦ f ≃ c x0 ◦ f = c cx0 elde edilir.
O halde f nullhomotoptur.

Tersine her Y uzay için Y → X tüm dönü³ümler nullhomotop ise, Y = X ald§mzda id X
dönü³ümünün nullhomotop oldu§u, yani X uzaynn büzülebilir oldu§u elde edilir.
8. X herhangi bir topolojik uzay, Y büzülebilir bir uzay ve [X, Y ], X ten Y uzayna sürekli dönü³ümlerin
homotopi snarnn kümesi olmak üzere [X, Y ] kümesinin tek elemanl oldu§unu gösteriniz.
Çözüm: Y bir büzülebilir uzay olsun. Bu durumda id Y : Y −→ Y birim dönü³üm ve her y ∈ Y
için f : Y −→ Y , f(y) = p ile tanml sabit dönü³üm olmak üzere H(y, 0) = id Y (y) ve H(y, 1) = f(y)
olacak ³ekilde H : Y × I −→ Y homotopi dönü³ümü vardr.
Herhangi bir α : X −→ Y sürekli dönü³ümü için G(x, t) = H(α(x), t) ile G : X ×I −→ Y dönü³ümünü
tanmlayalm.
• H ve α sürekli oldu§undan, G dönü³ümü de süreklidir.
• G(x, 0) = H(α(x), 0) = α(x) ve G(x, 1) = H(α(x), 1) = f(α(x)) = p
olup, α ≃ f. Her α : X −→ Y dönü³ümü p noktasnda sabit olan dönü³üme homotop oldu§undan [X, Y ]
nin tek elemanl oldu§u elde edilir.