Föreläsning 5

34 6 SAMBAND MELLAN DERIVATA OCH MONOTONITET
6. Samband mellan derivata och monotonitet
Antag att funktionen f är deriverbar på ]a,b[. Vi vet att derivatan f ′ (x 0 ) i x 0 ∈]a,b[ är
riktningskoefficienten för tangenten i punkten (x 0 ,f(x 0 )) till kurva y = f(x). Derivatan
f ′ (x 0 ) är därför ett mått på hur mycket funktionen förändras nära x 0 . Följande sats gäller:
Sats 6.1. Låt funktionen f vara deriverbar på ]a,b[. Då gäller att
(a) f ′ (x) = 0 för alla x ∈]a,b[ ⇔ f konstant på ]a,b[.
(b) f ′ (x) ≥ 0 för alla x ∈]a,b[ ⇔ f växande på ]a,b[.
(c) f ′ (x) > 0 för alla x ∈]a,b[ ⇒ f strängt växande på ]a,b[.
(d) f ′ (x) ≤ 0 för alla x ∈]a,b[ ⇔ f avtagande på ]a,b[.
(e) f ′ (x) < 0 för alla x ∈]a,b[ ⇒ f strängt avtagande på ]a,b[.
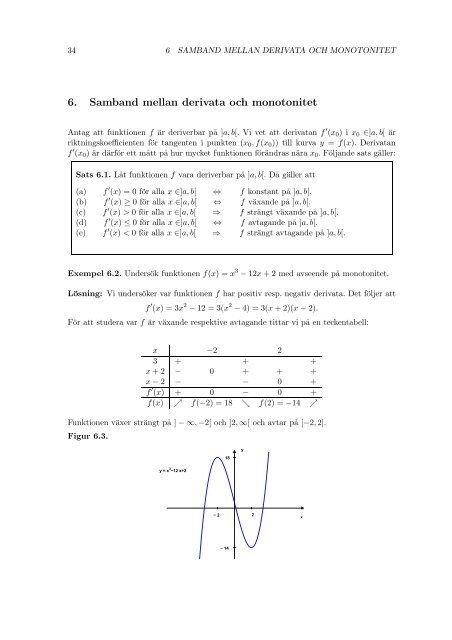
Exempel 6.2. Undersök funktionen f(x) = x 3 − 12x + 2 med avseende på monotonitet.
Lösning: Vi undersöker var funktionen f har positiv resp. negativ derivata. Det följer att
f ′ (x) = 3x 2 − 12 = 3(x 2 − 4) = 3(x + 2)(x − 2).
För att studera var f är växande respektive avtagande tittar vi på en teckentabell:
x −2 2
3 + + +
x + 2 − 0 + + +
x − 2 − − 0 +
f ′ (x) + 0 − 0 +
f(x) ր f(−2) = 18 ց f(2) = −14 ր
Funktionen växer strängt på ] − ∞, −2[ och ]2, ∞[ och avtar på [−2,2].
Figur 6.3.
18
y
y = x 3 −12 x+2
− 2 2
x
− 14

6.1 Lokala extrempunkter 35
6.1. Lokala extrempunkter
Definition 6.4. Låt f vara en funktionen definierad på ]a,b[. Vi säger att f har ett
lokalt maximum i x 0 ∈]a,b[ om
f(x) ≤ f(x 0 ) för alla x i närheten av x 0 .
Vi kallar då x 0 en lokal maximipunkt för f och funktionsvärdet f(x 0 ) för ett lokalt
maximivärde.
Observera: På motsvarande sätt definieras en lokal minimipunkt och ett lokalt minimivärde.
Lokala maximipunkter och lokala minimipunkter kallas med ett gemensamt
namn för lokala extrempunkter. Vi säger också att f har ett lokalt extremvärde i
dessa punkter.
Definition 6.5. Antag att funktionen f är deriverbar i punkten x 0 . Vi säger att punkten
x 0 är en stationärpunkt till f om
f ′ (x 0 ) = 0.
Exempel 6.6. Om f(x) = x 3 − 12x + 2, så är
f ′ (x) = 3x 2 − 12 = 3(x 2 − 4) = 3(x + 2)(x − 2) = 0 ⇔ x = ±2.
Funktionen f har alltså dem stationära punkterna x = ±2.
Satsen nedan ger oss ett effektivit sätt att söka efter lokala extrempunkter.
Sats 6.7. Om f har en lokal extrempunkt i x 0 ∈]a,b[ och om f är deriverbar i x 0 så
är f ′ (x 0 ) = 0, dvs extrempunkten x 0 är också en stationär punkt.
Bevis:

36 6 SAMBAND MELLAN DERIVATA OCH MONOTONITET
Exempel 6.8. Omvändningen till Sats 6.7 är inte sann, ty betrakta funktionen f(x) = x 3 .
Eftersom f ′ (x) = 3x 2 = 0 för x = 0 så är punkten x = 0 en stationär punkt. Vidare
gäller att f ′ (x) = 3x 2 > 0 för x ≠ 0, dvs f är strängt växande. Detta betyder att den
stationärapunkten x = 0 inte kan vara en extrempunkt.
Exempel 6.9. Bestäm alla lokala extrempunkter till f(x) = |x|(x − 2).
Lösning: Vi har att f(x) =
{ x(x − 2), x ≥ 0
−x(x − 2), x < 0
som är kontinuerlig för alla x.
Fallet x ≥ 0: Då är f(x) = x 2 − 2x och f ′ (x) = 2x − 2 = 0 om x = 1.
Fallet x < 0: Då är f(x) = −x 2 + 2x och f ′ (x) = −2x + 2 = 0 som saknar nollställen för
x < 0.
Dessutom ges höger derivatan i x = 0 av f +(0) ′ = lim − 2) = −2 och vänster derivatan
x→0 +(2x
är f − ′ (0) = lim + 2) = 2.
x→0−(−2x Alltså existerar ej f ′ (0) och funktionen är inte deriverbar i x = 0. Teckentabell visar
x 0 1
f ′ (x) + ∄ − 0 +
f(x) ր f(0) = 0 ց f(1) = −1 ր
Funktionen f har alltså en lokal maxpunkt i x = 0 och en lokal minpunkt i x = 1.
Figur 6.10.
y
y = |x| (x−2)
1 2
x

6.1 Lokala extrempunkter 37
Exempel 6.11. Bestäm alla lokala extrempunkter till f(x) =
{ xln x, x > 0
0, x = 0
Lösning: För x > 0 gäller att f ′ (x) = 1 + ln x = 0 om x = 1 . Vidare gäller också att
e
funktionen f är kontinuerlig för x ≥ 0. Speciellt gäller att lim xln x = 0 = f(0), dvs f är
x→0 +
kontinuerlig i x = 0. Däremot saknar f höger derivata, ty
Teckentabell ger
f(0 + h) − f(0) hln h
lim
= lim
h→0 + h h→0 + h
= lim ln h ej existerar.
h→0 +
x 0 1/e
f ′ (x) − 0 +
f(x) ց f(1/e) = −e ր
Funktionen f har alltså en lokal maxpunkt i x = 0 och en lokal minpunkt i x = 1/e.
Figur 6.12.
y
y = x ln x
1/e
− 1/e
x
Anmärkning:
• Exempel 6.8 visar att en stationär punkt inte behöver vara en extrempunkt.
• Exempel 6.9 visar att en punkt där funktionen inte är deriverbar kan vara en extrempunkt.
• Exempel 6.11 visar att en ändpunkt kan vara en extrempunkt.

38 6 SAMBAND MELLAN DERIVATA OCH MONOTONITET
Exempel 6.13. Bestäm eventuella lokala extrempunkter till funktionen
f(x) =
x
√
x 4 + 1 .
Lösning:

39
7. Tillämpningar på derivata
Som tillämpning på derivata kommer vi i det här avsnittet att studera största och minsta
värde hos en given funktion, grafritning, olikheter, ekvationer och medelvärdessatsen.
7.1. Medelvärdessatsen
Sats 7.1. Om f är kontinuerlig på [a,b] och deriverbar på ]a,b[, så finns minst ett
c ∈]a,b[ så att
f ′ f(b) − f(a)
(c) = .
b − a
Geometrisk tolkning:
Figur 7.2.
y
y = f(x)
a c 1
c 2 b
x
f(b) − f(a)
Kvoten är riktningskoefficienten för sekanten genom (a,f(a)) och (b,f(b)).
b − a
Medelvärdessatsen säger att det finns minst en punkt (c,f(c)) med en tangent parallell
med sekanten.

40 7 TILLÄMPNINGAR PÅ DERIVATA
( π
Exempel 7.3. Beräkna f om f(x) = cos x.
5)
( √
π 3
Lösning: Vi uttnyttjar att vi vet att f =
6)
2
( π
(
f(x) − f = f
6)
′ (c)
. Medelvärdessatsen ger att
x − π 6
där c ligger mellan x och π 6 . Sätter vi in x = π i uttrycket ovan får vi
5
( π
) ( π
(
f = f + f
5 6)
′ (c) x − π )
,
6
dvs
( π
( π
( π
cos = cos +
5)
6)
5 − π √
3
sin c =
6)
2 + π 30 sinc,
där c ligger mellan π 6 och π 5 . Antar vi nu att c ≈ π , så får vi att
6
( √
π 3
cos ≈
5)
2 + π ( π
) √
3
30 sin ≈
6 2 + π 1
30 2 ≈ 0,813.
)
,

7.1 Medelvärdessatsen 41
Exempel 7.4. Lös x = cos x 3 .
Lösning: Låt oss kalla roten till ekvationen för α, dvs α = cos α 3 . Eftersom cos x 3 är
kontinuerlig och avtar mellan 1 och 0 för 0 ≤ x ≤ 3π 2 så kommer kurvan y = cos x 3
och den
räta linjen y = α att skära varandra för något α som uppfyller 0 ≤ α ≤ 3π 2 . Låt x 0 vara en
godtycklig punkt sådan att 0 ≤ x 0 ≤ 3π 2
. Betrakta följande iterationsshema:
x n+1 = cos x n
3 , n = 0,1,2,... .
Vi visar att iteraten x n+1 går mot roten α, dvs x n+1 → α, då n → ∞. Enligt Medelvärdessatsen
finns ett c n mellan x n och α så att
|x n+1 − α| = |cos x n
3 − cos α 3 | = 1 3 |sin c n| · |x n − α|
≤ 1 3 |x n − α| ≤ 1 1
3 3 |x n−1 − α| = 1 3 2 |x n−1 − α| ≤ · · · ≤ 1
3 n+1 |x 0 − α| → 0,
då n → ∞. Detta ger att α ≈ 0.95.

42 7 TILLÄMPNINGAR PÅ DERIVATA
7.2. Största och minsta värde
Låt oss börja med att definiera vad vi menar med största och minsta värde hos en funktion.
Definition 7.5. Låt f vara en funktion. En punkt x 0 ∈ D f kallas en global maximipunkt
för f om
f(x 0 ) ≥ f(x) för alla x ∈ D f .
Talet f(x 0 ) kallas i så fall f:s största värde. Om istället
f(x 0 ) ≤ f(x) för alla x ∈ D f ,
kallas x 0 ∈ D f en global minimipunkt för f och f(x 0 ) f:s minsta värde.
Satsen nedan hjälper oss att söka efter punkter som ger största och minsta värde.
Sats 7.6. Om f är kontinuerlig på [a,b] så antar f sitt största respektive minsta värde
i någon av följande punkter:
1. i en inre punkt x ∈]a,b[ där f ′ (x) = 0,
2. i en inre punkt x ∈]a,b[ där f ′ (x) ej existerar,
3. i en randpunkt, dvs i x = a eller i x = b.
Följande sats kan vara användbar om det visar sig vara svårt att med hjälp av en teckentabell
avgöra karaktären hos en extrempunkt.
Sats 7.7. Antag att funktionen f är definierad nära punkten x 0 och att f ′′ (x 0 ) existerar.
Antag vidare att x 0 är en stationär punkt för f, dvs f ′ (x) = 0.
• Om f ′′ (x 0 ) > 0, så är x 0 en lokal minimipunkt för f
• Om f ′′ (x 0 ) < 0, så är x 0 en lokal maximipunkt för f

7.2 Största och minsta värde 43
Exempel 7.8. Bestäm största och minsta värde av funktionen f(x) = x 3 + 12|x|, där
−3 ≤ x ≤ 2.
Lösning: Funktionen f är kontinuerlig på ett slutet och begränsat intervall [−3,2].
Förutsättningarna för satsen om största och minsta värde, dvs Sats 2.16 är uppfyllda. Detta
betyder att f antar ett största och minsta värde på [−3,2]. Enligt Sats 7.6 hittar vi dessa
värden i en stationär punkt, en punkt där f är ej deriverbar eller i intervallets ändpunkter.
Vi börjar med att bestämma alla stationära punkter till f. Eftersom
f(x) = x 3 + 12|x| =
{ x 3 − 12x, −3 < x ≤ 0
x 3 + 12x, 0 < x ≤ 2
,
så är
f ′ (x) =
{ 3x 2 − 12, −3 < x < 0
3x 2 + 12, 0 < x < 2
Eftersom f ′ (x) = 3x 2 +12 > 0 för alla x saknar f stationära punkter i intervallet 0 < x < 2.
På intervallet −3 < x < 0 är f ′ (x) = 3x 2 −12 = 0 endast för x = −2. Vi har att f(−2) = 16.
Vidare gäller att punkten x = 0 är den enda punkt som funktionen f saknar derivata i. Vi
har f(0) = 0. Slutligen undersöker vi ändpunkterna; det gäller att f(−3) = 9 och f(2) = 32.
Alltså är största värde 32 för x = 2 och minsta värde är 0 för x = 0.
Figur 7.9.
y
y = x 3 + 12 |x|
32
16
9
− 3 − 2 − 1
1 2
x

44 7 TILLÄMPNINGAR PÅ DERIVATA
Exempel 7.10. Bestäm värdemängden till funktionen f(x) = xe −x , x ≥ 0. Hur många
gånger antas varje värde?
Lösning:

7.3 Grafritning 45
7.3. Grafritning
Antag att vi behöver rita grafen till en deriverbar funktion f. Vi skulle i så fall behöva
bestämma följande:
1. Extrempunkterna som återfinns bland de stationära punkterna.
2. Vågräta asymptoter som är räta linjer på formen y = A. Dessa finns om f har
ett gränsvärde, i så fall A, då x går mot ±∞, dvs om det finns ett A sådant att
lim f(x) = A.
x→±∞
3. Lodräta asymptoter som är räta linjer på formen x = a. Dessa finns om f har
det oegentliga gränsvärdet ∞ eller −∞ då x går mot punkten a, dvs
lim f(x) = ±∞.
x→a
4. Sneda asymptoter som är räta linjer på formen y = kx + m. Dessa linjer finns
om det finns tal k och m sådana att
f(x)
k = lim
x→±∞ x
och
m = lim (f(x) − kx).
x→±∞
Geometriskt betyder det att kurvan y = f(x) och linjen y = kx+m går närmare
och närmare varandra då x → ±∞, dvs
lim (f(x) − kx − m) = 0.
x→±∞

46 7 TILLÄMPNINGAR PÅ DERIVATA
Exempel 7.11. Rita grafen till funktionen y = x2 + 1
x 2 , så att alla väsentliga drag framgår.
− 4
Lösning: y = x2 + 1
x 2 − 4 ⇒ y′ = −
10x
(x 2 − 4) 2. Varken y eller y′ är definierade för x = ±2 och
dessutom har vi att y → ±∞ då x → ±2, d.v.s. vi har lodräta asymptoter i x = ±2. Vidare
ser vi att y ′ = 0 ⇒ x = 0. Teckentabellen blir då
x −2 0 +2
−10x + + + 0 − − −
(x 2 − 4) 2 + 0 + + 0 +
y ′ + ∄ + 0 − ∄ −
y ր ∄ ր y(0) ց ∄ ց
Vi har alltså ett lokalt maximum i x = 0 med y(0) = − 1 , och lokalt minimum saknas.
4
För att undersöka vågräta asymptoter studerar vi
lim y = lim x 2 + 1
x→±∞ x→±∞ x 2 − 4 = lim 1 + 1
x 2
x→±∞ 1 − 4 = 1.
x 2
En sned asymptot y = kx + m finns inte då eftersom
y
k = lim
x→±∞ x = lim x 2 + 1
x→±∞ x(x 2 − 4) = 0.
Dessutom kan vi notera att y → +∞ då x → −2 − och x → +2 + , samt y → −∞ då
x → −2 + och x → +2 − .
Svar: Lokalt max i (0, −1/4), lokalt min saknas. Lodräta asymptoter för x = ±2. Vågrät
asymptot y = 1 då x → ±∞.
Figur 7.12.
y
y = (x 2 +3) / (x 2 −4)
x

7.3 Grafritning 47
Exempel 7.13. Bestäm alla sneda asymptoter till kurvan f(x) = x + arctan x.
Lösning: Linjen y = kx + m är en sned asymptot till kurvan y = f(x) om det finns tal k
och m sådana att
f(x)
k = lim
x→±∞ x
och
m = lim (f(x) − kx).
x→±∞
Det följer att
f(x)
x
= x + arctan x
x
Detta ger att k = 1. Vidare gäller att
= 1 + arctan x
x
→ 1, då x → ±∞.
{ π/2, då x → +∞
f(x) − kx = (x + arctan x) − 1 · x = arctan x →
−π/2, då x → −∞
Alltså, har kurvan de sneda asymptoterna y = x + π 2 respektive y = x − π 2 .
Figur 7.14.
y
y = x + arctan x
x

48 7 TILLÄMPNINGAR PÅ DERIVATA
Exempel 7.15. Rita f(x) = x + 1 + 2arctan x. Ange lokala extrempunkter, största och
x − 1
minsta värde samt lodräta och vågräta asymptoter.
Lösning:

7.4 Olikheter 49
7.4. Olikheter
Exempel 7.16. Visa att xln x − (ln x) 2 ≥ x − 2 för x ≥ 1.
Lösning: Självklart ska man rita funktionerna och se att grafen till xln x − (ln x) 2 ligger
ovanför grafen till x − 2. Men det räcker inte som bevis. Vad man ska göra är att bilda en
funktion f som skillnaden mellan funktionerna, t.ex. om vi bildar funktionen
f(x) = xln x − (ln x) 2 − x + 2,
så är vi klara om vi kan visa att f(x) ≥ 0 för x ≥ 1.
Låt oss studera funktionen f(x). Vi deriverar funktionen f(x) för x > 1 och får
f ′ (x) = ln x + 1 − 2 1 x
ln x − 1 =
xln x − 2ln x
x
=
(x − 2)ln x
x
= 0 för x = 2.
En teckentabell blir
x 1 2
f ′ (x) − 0 +
f(x) ց ր
Funktionen f har alltså ett minsta värde f(2) = 2ln 2 − (ln 2) 2 = (2 − ln 2)ln 2 > 0.
Dessutom har vi att
och
lim f(x) = lim
x→1 + x→1 +(xln x − (ln x)2 − x + 2) = 1 > 0,
f(x) = xln x − (ln x) 2 − x + 2 → ∞, då x → ∞.
Alltså är f(x) ≥ 0 för x ≥ 1 och därmed klara.
Figur 7.17.
y
f(x) = x ln x − ( ln x ) 2 − x + 2
2 ln 2 − ( ln 2 ) 2
2
x

50 7 TILLÄMPNINGAR PÅ DERIVATA
Exempel 7.18. Visa att arctan x ≥
Lösning:
x
x + 1
för x > −1.

7.5 Ekvationer 51
7.5. Ekvationer
Exempel 7.19. Hur många rötter har ekvationen 2x − xln x = 1 i intervallet 0 < x < 1.
(Observera att vi bestämmer antalet och inte deras värden).
Lösning: Vi bildar en funktion som är skillnaden mellan leden. Betrakta funktionen
f(x) = 2x − xln x = 1 för 0 < x < 1.
Problemet att bestämma antalet rötter till ekvationen är detsamma som att bestämma
antalet nollställen till f(x). Produktregeln ger
f ′ (x) = 2 − ln x − x 1 x = 1 − ln x > 0
för 0 < x < 1, ty ln x < 0 för 0 < x < 1. Alltså är f(x) strängt växande och kan ha högst
ett nollställe, dvs ekvationen kan ha högst en rot.
Vidare gäller att
f(x) = lim − xln x − 1) = −1,
+ +(2x
och
lim
x→0
lim
x→1
x→0
f(x) = lim − xln x − 1) = 1.
− −(2x
x→1
Eftersom f är kontinuerlig så säger satsen om mellanliggande värden att till ett y = 0 som
ligger mellan y = −1 och y = 1 finns minst ett c där 0 < c < 1, så att f(c) = 0. Detta c
är ett nollställe till f, dvs ekvationen högst en rot. Högst ett nollställe tidigare kombinerat
med minst ett nollställe ger nu exakt ett nollställe.
Ekvationen har alltså precis en rot i 0 < x < 1.
Figur 7.20.
y
f(x) = 2 x − x ln x − 1
c
1
x

52 7 TILLÄMPNINGAR PÅ DERIVATA
Exempel 7.21. Hur många reella lösningar har ekvationen ln 4 + 16x2
5
= arctan 2x?
Lösning:

7.5 Ekvationer 53
Exempel 7.22. Bestäm för varje värde på konstanten a antalet skilda reella rötter till
ekvationen x 3 − 12x = a.
Lösning: Vi studerar funktionen f(x) = x 3 − 12x och jämför sedan med linjen y = a. Det
gäller att
f ′ (x) = 3x 2 − 12 = 3(x 2 − 4) = 3(x + 2)(x − 2) = 0 ⇔ x = ±2.
Teckentabell:
x −2 2
3 + + +
x + 2 − 0 + +
x − 2 − − 0 +
f ′ (x) + 0 − 0 +
f(x) ր ց ր
Dessutom gäller att
och
f(x) = x 3 − 12x → ∞, då x → ∞
f(x) = x 3 − 12x → −∞, då x → −∞.
Funktionen f:s största värde är f(−2) = 16 och minsta värde är f(2) = −16.
Satsen om mellanliggande värden säger att ekvationen har:
1. en rot om a < −16 eller a > 16,
2. två rötter om a = ±16,
3. tre rötter om −16 < a < 16,
y = (x 3 −12 x)
y
En rot om a>16
Två rötter om a=16
Tre rötter om −16 < a < 16
x

54 7 TILLÄMPNINGAR PÅ DERIVATA