Lösningsförslag!
Lösningsförslag!
Lösningsförslag!
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
TEKNISKA HÖGSKOLAN i LINKÖPING TENTAMEN - TMHL08<br />
Hållfasthetslära/IKP<br />
Finita Elementmetoden; grundkurs<br />
Bo Torstenfelt 2006-08-22<br />
Lösningsförslag!<br />
Tentamen i hållfasthetslära<br />
Finita Elementmetoden; grundkurs<br />
2006-08-22 kl. 14-18<br />
Bo Torstenfelt träffas under skrivtiden på telefon 281109. Resultatet anslås senast<br />
2006-09-07 på anslagstavlan, ingång 15, B-korridoren. Rätta lösningar anslås på<br />
anslagstavlan efter skrivtidens slut.<br />
Granskningstiden utgår 2006-09-21.<br />
Betyg: 3 4 5<br />
Poäng: 6-8 9-11 12-16<br />
På del I (teoridelen) får inga hjälpmedel användas. Frågorna besvaras direkt på<br />
tesen. Tentanden avgör själv när han/hon vill lämna in del I. Detta meddelas<br />
till vakthavande genom att eleven räcker upp handen. Tentanden får då ut del II<br />
(problemdelen) och får då ta fram hjälpmedel enligt nedanstående:<br />
Formelsamling i Hållfasthetslära, KTH<br />
T Dahlberg, formelsamling i Hållfasthetslära,<br />
Supplement till Teknisk Hållfasthetslära, Studentlitteratur, Lund<br />
Standard Math Tables<br />
Beta, Tefyma, Physics Handbook<br />
Introduction to the Finite Element Method<br />
Räknedosa
TEKNISKA HÖGSKOLAN i LINKÖPING TENTAMEN - TMHL08<br />
Hållfasthetslära/IKP<br />
Finita Elementmetoden; grundkurs<br />
Bo Torstenfelt 2006-08-22<br />
Del I (teoridel)<br />
Namn: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .<br />
1. Nämn minst 2 delsteg vilka alltid kan identifieras vid omformulering av ett Randvärdesproblem<br />
till dess motsvarande ekvivalenta Svaga form.<br />
(1p)<br />
• Multiplikation med en viktfunktion<br />
• Integration över området<br />
• (Partiell integration)
TEKNISKA HÖGSKOLAN i LINKÖPING TENTAMEN - TMHL08<br />
Hållfasthetslära/IKP<br />
Finita Elementmetoden; grundkurs<br />
Bo Torstenfelt 2006-08-22<br />
Del I (teoridel)<br />
Namn: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .<br />
2. Vid FE-analys av balkproblem mha den typ av balkelement vi studerat erhålls<br />
kontinuitet över elementgränserna hos två av de sökta storheterna. Vilka är dessa<br />
storheter?<br />
(1p)<br />
Förskjutning och lutning hos balkens medellinje är kontinuerliga<br />
över elementgränserna.
TEKNISKA HÖGSKOLAN i LINKÖPING TENTAMEN - TMHL08<br />
Hållfasthetslära/IKP<br />
Finita Elementmetoden; grundkurs<br />
Bo Torstenfelt 2006-08-22<br />
Del I (teoridel)<br />
Namn: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .<br />
3. Studera ett 3D värmeledningsproblem. Hur många differentialekvationer finner<br />
man hos motsvarande randvärdesproblem.<br />
(1p)<br />
1
TEKNISKA HÖGSKOLAN i LINKÖPING TENTAMEN - TMHL08<br />
Hållfasthetslära/IKP<br />
Finita Elementmetoden; grundkurs<br />
Bo Torstenfelt 2006-08-22<br />
Del I (teoridel)<br />
Namn: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .<br />
4. Vad är grundide´n vid en iso-parametrisk elementstyvhetsmatrisformulering!<br />
(1p)<br />
Att förskjutning och geometri interpoleras på samma sätt.<br />
u = Na och x = Nc där N ≡ N
TEKNISKA HÖGSKOLAN i LINKÖPING TENTAMEN - TMHL08<br />
Hållfasthetslära/IKP<br />
Finita Elementmetoden; grundkurs<br />
Bo Torstenfelt 2006-08-22<br />
Del II (problemdel)<br />
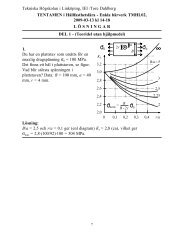
5. Tre elastiska stänger är sammanfogade enligt figuren nedan. Bestäm förskjutningen<br />
under kraften P samt kontrollera att jämvikten är uppfylld!<br />
(3p)<br />
E, A, 2L<br />
E<br />
2 A<br />
2 L<br />
P<br />
E<br />
2 A<br />
2 L<br />
v 1<br />
u 1 1<br />
1 2<br />
2<br />
3<br />
3<br />
v 3<br />
v 2<br />
u 3<br />
u 2<br />
Gör följande frihetsgradsuppdelning.<br />
⎧<br />
⎪⎨<br />
a L =<br />
{<br />
u2<br />
v 3<br />
}<br />
; a S =<br />
⎪⎩<br />
Bilda elementstyvhetsmatriserna<br />
⎡<br />
⎤<br />
1 0 −1 0<br />
K e 1 = EA<br />
⎢ 0 0 0<br />
⎥<br />
2L ⎣ 1 0 ⎦<br />
0<br />
u 1<br />
v 1<br />
v 2<br />
u 3<br />
⎫⎪ ⎬<br />
⎪ ⎭<br />
= 0<br />
K e 2 = EA<br />
2L<br />
⎡<br />
⎢<br />
⎣<br />
1 −1 −1 1<br />
1 1 −1<br />
1 −1<br />
1<br />
⎤<br />
⎥<br />
⎦ ;<br />
Ke 3 = EA<br />
2L<br />
⎡<br />
⎢<br />
⎣<br />
1 1 −1 −1<br />
1 −1 −1<br />
1 1<br />
1<br />
⎤<br />
⎥<br />
⎦<br />
Assemblera följande system.<br />
[ ] { } { }<br />
KLL K LS aL f<br />
= L<br />
K SS a S f S<br />
K T LS
a L = K −1<br />
LL f L och f S = K T LSa L ty a S = 0<br />
⇒<br />
EA<br />
2L<br />
[<br />
2 −1<br />
−1 2<br />
] { }<br />
u2<br />
=<br />
v 3<br />
{ 0<br />
−P<br />
}<br />
{ }<br />
u2<br />
= 1 [ 2 1<br />
v 3 3 1 2<br />
] {<br />
0<br />
−2P L/EA<br />
}<br />
= − 2P L<br />
3EA<br />
{ 1<br />
2<br />
}<br />
Bestäm reaktionskrafterna f s<br />
⎡ ⎤<br />
−1 1<br />
f S = EA<br />
⎢ 0 −1<br />
⎥<br />
2L ⎣ 1 −1 ⎦<br />
−1 0<br />
{<br />
u2<br />
v 3<br />
}<br />
= − P 3<br />
⎧<br />
⎪⎨<br />
⎪⎩<br />
1<br />
−2<br />
−1<br />
−1<br />
⎫<br />
⎪⎬<br />
⎪⎭<br />
2P/3<br />
P/3<br />
P/3<br />
P/3<br />
P<br />
SVAR:<br />
{<br />
u2<br />
v 3<br />
}<br />
= − 2P L<br />
3EA<br />
{ 2<br />
1<br />
}<br />
; f S = − P 3<br />
⎧<br />
⎪⎨<br />
+ Samtliga jämviktsekvationer är satisfierade.<br />
⎪⎩<br />
1<br />
−2<br />
−1<br />
−1<br />
⎫<br />
⎪⎬<br />
⎪⎭
TEKNISKA HÖGSKOLAN i LINKÖPING TENTAMEN - TMHL08<br />
Hållfasthetslära/IKP<br />
Finita Elementmetoden; grundkurs<br />
Bo Torstenfelt 2006-08-22<br />
Del II (problemdel)<br />
6. En rak L lång elastisk balk är belastad med en jämnt utbredd last/l.e. med en<br />
total resultant Q. Balken är fast inspänd i den vänstra änden och fri i den högra.<br />
Applicera sedan också ett böjande moment M i balkens högra ände. Bestäm detta<br />
moment så att lutningen vid den högra änden blir lika med noll. Det räcker att<br />
använda endast ett element.<br />
(3p)<br />
Q<br />
E, I, L<br />
θ<br />
w<br />
M<br />
Använd endast ett element<br />
⎡<br />
⎤<br />
−<br />
K e = EI<br />
⎢ −<br />
⎥<br />
L 3 ⎣ 12 −6L ⎦ (17.66)<br />
4L 2<br />
Den utbredda lasten ger 17.71<br />
⎧<br />
⎪⎨<br />
f e = Q 2<br />
⎪⎩<br />
−<br />
−<br />
−1<br />
L/6<br />
⎫<br />
⎪⎬<br />
⎪⎭<br />
Assemblering ⇒<br />
EI<br />
L 3 [ 12 −6L<br />
−6L 4L 2 ] { w<br />
θ<br />
} {<br />
=<br />
−Q/2<br />
M + QL/12<br />
}<br />
{ w<br />
θ<br />
}<br />
= L [ 4L<br />
2<br />
−6L<br />
12EI 6L 12<br />
] {<br />
−Q/2<br />
M + QL/12<br />
}
M fås ur θ = 0 ⇒<br />
−3QL + 12M + QL = 0<br />
SVAR:<br />
M = QL<br />
6
TEKNISKA HÖGSKOLAN i LINKÖPING TENTAMEN - TMHL08<br />
Hållfasthetslära/IKP<br />
Finita Elementmetoden; grundkurs<br />
Bo Torstenfelt 2006-08-22<br />
Del II (problemdel)<br />
7. Ett värmeledande område är rotationssymmetriskt runt z-axeln. I vänstra änden<br />
är temperaturen 10. ◦ C (Nod 1) och i den högra änden 0. ◦ C (Nod 4). Beräkna<br />
temperaturerna i noderna 2 och 3 mha en 1D värmeledningsanalys. Mantelytan<br />
kan antas vara en isolerad rand. Kroppen har isotropa värmeledningsegenskaper<br />
med ett värmeledningstal λ = 2.J/ ◦ Cms. Geometrin är definerad mha de ofyllda<br />
ringarna nedan (Mellan ringarna varierar radien r linjärt map z).<br />
(3p)<br />
r<br />
(10; 20)<br />
L = 20.<br />
(30; 14)<br />
(50; 10)<br />
(70; 8)<br />
1<br />
1 2 3<br />
2<br />
3<br />
4<br />
z<br />
Elementstyvhetsmatrisen K e fås ur<br />
K e i =<br />
∫ zi+1<br />
z i<br />
B eT λB e A(z)dz<br />
där<br />
⇒<br />
där<br />
B e = 1 L<br />
K e i = λa i<br />
L 2 [<br />
a 1 = π<br />
[<br />
−1 1<br />
]<br />
∫ 30<br />
10<br />
1 −1<br />
−1 1<br />
]<br />
(23 − 3z<br />
10 )2 dz<br />
i = 1, 2, 3<br />
a 2 = π<br />
∫ 50<br />
30<br />
(20 − 2z<br />
10 )2 dz<br />
a 3 = π<br />
∫ 70<br />
50<br />
(15 − z 10 )2 dz
Assemblering ⇒ följande system<br />
⎡<br />
⎤ ⎧<br />
a 1 −a 1 0 0<br />
λ<br />
⎢ a 1 + a 2 −a 2 0<br />
⎪⎨<br />
⎥<br />
L 2 ⎣<br />
a 2 + a 3 −a 3<br />
⎦<br />
⎪⎩<br />
a 3<br />
10<br />
T 2<br />
T 3<br />
0<br />
⎫ ⎧<br />
⎪⎬ ⎪⎨<br />
=<br />
⎪⎭ ⎪⎩<br />
?<br />
0<br />
0<br />
?<br />
⎫<br />
⎪⎬<br />
⎪⎭<br />
ekvation 2 och 3 ⇒<br />
[<br />
a1 + a 2 −a 2<br />
−a 2<br />
a 2 + a 3<br />
] {<br />
T2<br />
T 3<br />
}<br />
=<br />
{ 10a1<br />
0<br />
}<br />
Vilket har lösningen<br />
{ }<br />
T2<br />
10a 1<br />
=<br />
T 3 (a 1 + a 2 )(a 2 + a 3 ) − a 2 2<br />
Efter lösning av integralerna a 1 , a 2 och a 3 fås<br />
{ }<br />
a2 + a 3<br />
a 2<br />
SVAR:<br />
{<br />
T2<br />
}<br />
≈<br />
T 3<br />
{ 8.485<br />
5.440<br />
Om areorna vid respektive mittpunkt används<br />
{ } { }<br />
T2 8.5<br />
≈<br />
T 3 5.4<br />
}
TEKNISKA HÖGSKOLAN i LINKÖPING TENTAMEN - TMHL08<br />
Hållfasthetslära/IKP<br />
Finita Elementmetoden; grundkurs<br />
Bo Torstenfelt 2006-08-22<br />
Del II (problemdel)<br />
8. Betrakta ett 2D elasticitetsproblem. Området är triangulärt med konstant tjocklek<br />
t enligt figuren nedan. I övre hörnet angriper en horisontell koncentrerad kraft P.<br />
De båda övriga hörnen är fast inspända. Modellera området med ett enda 3-<br />
nodigt finit element och beräkna förskjutningen under kraften! E-modulen E och<br />
Poisson´s ν = 0.5 kan antas givna.<br />
(3p)<br />
v 3<br />
u 3<br />
(7; 6)<br />
3<br />
P<br />
(2; 4)<br />
1<br />
E, ν, t<br />
y<br />
2<br />
(8; 1)<br />
x<br />
Beräkna elementstyvhetsmatrisen<br />
∫<br />
K e = B eT DB e tdA (16.66)<br />
A α<br />
där<br />
⎡<br />
B e = 1 ⎣<br />
2A α<br />
y j − y k 0 y k − y i 0 y i − y j<br />
⎤<br />
0 x k − x j 0 x i − x k 0 x j − x i<br />
⎦ (15.23)<br />
2A α = (x j y k − x k y j ) − (x i y k − x k y i ) + (x i y j − x j y i ) (7.89)<br />
A α = 27/2<br />
Och om P.S antages<br />
⎡<br />
D =<br />
E ⎣<br />
1 − ν 2<br />
1 ν 0<br />
1 0<br />
(1 − ν)/2<br />
⎤<br />
⎦ = E 3<br />
⎡<br />
⎣<br />
4 2 0<br />
2 4 0<br />
0 0 1<br />
⎤<br />
⎦ ν = 0.5 (13.33)
Ovan ⇒<br />
⇒<br />
⎡<br />
B e = 1 ⎣<br />
2A α<br />
DB e =<br />
K e =<br />
⎡<br />
E ⎣<br />
6A α<br />
⎡<br />
Et<br />
12A α ⎢<br />
⎣<br />
−5 0 2 0 3 0<br />
0 −1 0 −5 0 6<br />
−1 −5 −5 2 6 3<br />
⎤<br />
⎦<br />
−20 −2 8 −10 12 12<br />
−10 −4 4 −20 6 24<br />
−1 −5 −5 2 6 3<br />
− − − − − −<br />
− − − − −<br />
− − − −<br />
− − −<br />
72 54<br />
153<br />
⎤<br />
⎥<br />
⎦<br />
⎤<br />
⎦<br />
Lös följande system<br />
[<br />
Et 72 54<br />
12A α 54 153<br />
{<br />
u3<br />
v 3<br />
}<br />
] { } {<br />
u3 P<br />
=<br />
v 3 0<br />
= 12P A [<br />
α 153 −54<br />
Et · 8100 −54 72<br />
}<br />
] { 1<br />
0<br />
}<br />
SVAR:<br />
{ }<br />
u3<br />
= P { 153<br />
v 3 50Et −54<br />
}