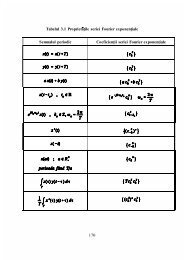
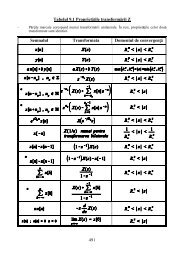
Transformata Laplace

Transformata LaplaceTransformata Laplace generalizează ideea transformatei Fourier in tot planul complex.Pt un semnal x(t) spectrul sau transformata Fourier este∞− jωt( ω) ( )X = ∫ xte dtPt acelaşi semnal x(t) se poate introduce transformata Laplace−∞( ) ( ) ( )∞−stL x() t () s = X s = ∫ x t e dt;s = σ + jω−∞unde integrala se efectuează pe o curba σ = cst de la −∞ la ∞ .Pentru σ = 0 transformata Laplace este spectrul semnalului adică transformata Fourier.σ=cstjωσDomeniul de convergenta = domeniul valorilor lui s pt care integrala este convergentasau X(s) - finita.Proprietati DC1. format din benzi paralele cu axa imaginara jω2. nu conţine nici un pol al transformatei Laplace3. pt semnale cu întindere spre dreapta (o subcategorie fiind semnalele cauzale), DCîncepe cu cel mai dreapta pol si se întinde tot spre dreapta Re{ s } >σp max4. pt semnale cu întindere spre stânga (o subcategorie fiind semnalele anticauzale),DC începe cu cel mai dreapta pol si se întinde tot spre stânga Re{ s }

Transformata inversa∞1stx() t = X ( s)e ds2πj∫−∞Integrala se efectuează pe dreapta paralela cu axa imaginara ( σ = cst )Mai des se foloseşte metoda descompunerii in fracţii simple si inversarea cu ajutorultabelelor.Problemes + 21. Transformata Laplace X(s) a unui semnal x(t) este X()s =.2( s− 1) ( s+3)Sa se determine x(t) in următoarele condiţiia) Re(s) B= ( s+ 3) X( s) = =−1/16s=−32( s −1)s + 2A = s− X s = =2s=−32( 1) ( ) 3/4s=1s + 3s=1d s+ 3−s−2A = ⎡( s− 1) X( s) ⎤ = = 1/1621 2ds ⎣ ⎦s= 1( s + 3)s=1s + 2 1/16 3/ 4 1/16X()s = = + −( s− 1) 2 ( s+3) s-1 s+3( s-1) 2t t 3ta) DC : Re(s) x()t =− eσ ( −t) − teσ ( − t) + e − σ ( −t);1 3 116 4 161 3 116 4 16t t 3tb) DC: -3< Re(s) x()t =− eσ ( −t) − teσ ( −t) − e − σ () t1 3 116 4 16t t 3tc) DC: Re(s) > 1 => x()t = eσ () t + teσ () t − e − σ () tVerificati expresia lui x(t) folosind mediul Matlab:>> L=(s+2)/((s-1)^2*(s+3))>> ilaplace(L)2

2. Funcţia de transfer a unui sistem liniar invariant in timp si cauzal este data de expresias + 2H()s = . Determinaţi si desenaţi răspunsul sistemului, daca la intrarea sa se2s + 2s+ 22 taplica semnalul x()t = e −.Rezolvarey t = x t ∗y t ↔ Y s = X s ⋅ H s() () () ( ) ( ) ( )s+ 2 s+2H()s = =cu poli complecşi s 1,2= − 1± j ⇒σp max=− 12 2 ( )( )2s + s+ s−s1 s−s2jω-21DC pentru H(s)σ-1-1Sistemul este cauzal: DC este Re{ s } >− 1−2t−2 t ⎧e, t ≥ 0 −2t 2tx()t = e = ⎨ = e σ () t + e σ ( −t)2t⎩ e , t < 01 1 −4=> X()s = − = cu DC: -2 s= 2, A = -2/5s=0, C = 8/5s=1, B = 2/52 1 2 s+ 4 2 1 2⎡s+1 3=− + =− + ⎢ +s s s s ⎢⎣( s ) ( s )2 2() 2 t −t −ty t = e σ − t + ⎡e cost+3e sint⎤σt5 5⎣ ⎦=> Y( s)22 25 − 2 5 + 2 + 2 5 − 2 5 + 1 + 1 + 1 + 1=> ( ) ()⎤⎥⎥⎦X s :3

3. Fie un sistem liniar, invariant in timp si cauzal a cărui funcţie de sistem H(s) areconstelaţia de poli si de zerouri din figura:jω-3-11 2σa) Sa se indice toate regiunile de convergenta posibile; b) Indicaţi in fiecare caz dacasistemul satisface sau nu condiţiile de stabilitate si/sau cauzalitate.Rezolvare.Re(s) sistem anticauzal si instabil,-3

a) Determinaţi H(s), funcţia de transfer a sistemului. Schiţaţi constelaţia de poli sizerouri.b) Determinaţi h(t) daca – sistemul este stabil; - sistemul este cauzal; - sistemul nueste nici stabil nici cauzal.Rezolvare.2dd2a) x() t ↔ sX ( s) ; x2() t ↔ s X ( s).dtdt21 1 A B=> sY+ 2sY− 3Y= X => H( s)= = = +2s + 2s−3 ( s− 1)( s+ 3)s− 1 s+31 1A= ( s− 1) H( s)= =s=1s + 3s=141 1B = ( s+ 3) H( s)= =−s=−3s −1 4( )H s1⎛1 1 ⎞= ⎜ − ⎟4⎝s− 1 s+3⎠s=−3jω-31σ1 14 4ht1 t 1 −3t= eσt− e σ t4 4(instabil)t−3tb) sistem stabil DC: -3> L=1/4/(s-1)-1/4/(s+3)>> ilaplace(L)1 14 4t−3tsistem instabil,anticauzal DC: Re(s)

) determinaţi funcţia pondere a sistemului, h(t)c) care este ecuaţia diferenţiala care descrie sistemul,d) daţi o implementare posibila a sistemului.Rezolvare.2 2 1 1a) Y( s) = − X ( s)= +s+ 1 s+ 4 s+ 1 s+ 3;Y( s)6 ( s+ 1)( s+ 3)3( s+3)H( s)= = =X ( s) ( s+ 1)( s+ 4)2( s+ 2)( s+ 2)( s+4)3( jω+ 3)H( ω) = H( s)=s=jω( jω+ 2)( jω+4)3( s + 3)A Bb) H( s)= = +( s+ 2)( s+ 4)s+ 2 s+43( s + 3)3A= ( s+ 2 ) H( s)= = ; B ( s 4 ) H( s)s=−2s + 4 2s=−23⎛1 1 ⎞ 3H s ⎜⎟ h t e e t2⎝s+ 2 s+4⎠2−2t−4t( ) = + ↔ () = ( + ) σ (); DC: Re(s)>-2, sistem cauzal( s + )3 3 3= + = =s=−4s + 2 2Verificati expresia raspunsului la impuls folosind mediul Matlab:>> L=(3/2)/(s+2)+(3/2)/(s+4)>> ilaplace(L)Mkk kbsNMkd y d x Y( s)∑k = 0∑ k=k ∑ k↔ = =kNk= 0 dt k=0 dt X ( s)k∑ askk = 0c) Ecuaţia diferenţiala a b H( s)=> y′′ + 6y′ + 8y = 3x′+ 9xd) Se foloseşte una din cele 2 forme canonice de implementare:ay+ ay′ + ay′′ = bx+ bx′ + bx′′0 1 2 0 1 2∫ ∫a y+ a y+ a y′ = b x+ bx+b x′0 1 2 0 1 2∫∫ ∫ ∫∫ ∫a y+ a y+ a y = b x+ b x+b x0 1 2 0 1 21y ⎡b x b x b x a y a y⎤∫∫ ∫ ∫∫ ∫ ⎦=> =0+1+2−0−1a ⎣2 0s=−46

Forma canonică 1 Forma canonică 21/a 2x b 2yx 1/a 2 b 2∫∫b 1b 0-a 1-a 0∫∫y∫-a 1 b 1∫-a 0 b 0x 1∫-6 3y∫-8 98. Pentru sistemul liniar si invariant in timp cauzal cu răspunsul in frecventa7 + jωH ( ω)=2( 4+ jω )( 1− ω + jω)a) determinaţi h(t),b) daţi o structura de implementare constând din doua sisteme conectate in cascada,c) daţi o structura de implementare constând din doua sisteme conectate in paralel.Rezolvare.s+ 7 A Bs+CH( s) = H( ω )s == = +jωs+ s + s+2( s+ 4)( s + s+1)s + 7 3A= ( s+ 4 ) H( s)= =s=−42s + s+1s=−413s=0 => C=22/13 => B=-3/13.24 17

( )H s( )H s( )H s⎛ 22 ⎞⎛22 ⎞3 ⎜ s−1 3 ⎟⎜ s−⎟3 1= 3⎜ −2 ⎟= ⎜ −⎟213 ⎜s+ 4 s + s+ 1⎟13 ⎜s+ 4 ⎛ 1⎞3 ⎟s⎝ ⎠⎜ ⎜ + ⎟ + ⎟⎝ ⎝ 2⎠4 ⎠⎛1 22 1 ⎞⎜ s ++ ⎟3 1= ⎜ − 2 + 3 2 ⎟2 213 ⎜s+ 4 ⎛ 1⎞ 3 ⎛ 1⎞3 ⎟⎜ ⎜s+ ⎟ + ⎜s+ ⎟ + ⎟⎝ ⎝ 2⎠ 4 ⎝ 2⎠4 ⎠⎛⎜1 3s3 ⎜+1 2 47 2= 2⎜ − +13⎜s + 4 ⎛ 1⎞ 3 6 3s1 ⎛ 3⎞+ + ⎛ ⎞⎜ ⎜ ⎟ s + +2 4 ⎜ ⎟⎝ ⎠⎜ ⎟⎝⎝ 2⎠ ⎝ 2 ⎠2 223 3 3 3 47 3ht e t e t t e t t13 13 2 13 3 3 2−() 4 t −t () /2 −t= σ − cos σ () +/2 sin σ ()Verificati expresia raspunsului la impuls folosind mediul Matlab:b) ( )>> L=(s+7)/(s+4)/(s^2+s+1)>> ilaplace(L)s+ 7 1 s+7H s = = = H () ()2as Hbss+ 4 s + s+12( s+ 4)( s + s+1)Pentru H a (s): ay0+ ay′ 1= bx0+ bx′ 1sau 4y+ y′= xPentru H b (s): ay0+ ay′ 1+ ay′′ 2= bx0+ bx′ 1+ bx′′ 2sau y+ y′ + y′′ = x′+ 7x⎞⎟⎟⎟⎟⎟ ⎠x 1∫-4 uu 1∫-1 1∫-1 7y8

1Ab) H ( ω) = ==> A=1, amplificare la joasa frecventa2 2 21− ω + 3jω ω0 − ω + 2jξωω01Q = 0.332ξ= , factorul de calitate, ω = 1 pulsaţia naturala01 1c) H( s)= 2s 3s 1=− 3±5, s1,2= ,+ + s−s s−s2( )H sA B= +s−s s−s1 2=> A ( s s ) H( s)( )( )1 21 2 1 5= −1= = = =s=s1s− s − 3+ 5 −( −3−5) 5 5=> B ( s s ) H( s)2s=s11 2 1 5= −2= = =− =−s=s2s− s −3− 5 −( − 3+5) 5 551 s=s−st1 −s2t=> ht () = ⎡e σ () t−e σ () t⎤5 ⎣⎦Răspunsul sistemului la impulsul unitate, x( t) = δ ( t)=> y ( t) = h( t)Răspunsul sistemului la x() t = A0cosω0t=>( { })() = ( ω ) cos ω + arg ( ω )y t A H t HH( ω)0 0 0 01 1= ⇒ H( ω ) =1− ω + 9ω 1− ω + 9ω( )2{ H( ω)} =− { − ω + jω}arg arg 1 3Daca012( )202 2 2220 0ω < atunci H ( ω )Daca01ω > atunci ( )3ω0arg{ 0 } =−arctg 21 −ω03ω0arg{ H ω0} = π + arctg21 −ω10. Pentru un SLIT răspunsul in frecventa este H ( ω)a) Sa se determine răspunsul la impuls al sistemului h(t),b) Daţi o structura de implementare a sistemului.a) H( s)5s+ 7 1 s+2= =− +s+ s + s+2( s+ 4)( s + s+1)24 10=5jω+ 7jω+ 4 jω + jω+1( ) ( )2( ).10

1 3s +1 2 4s + 4 ⎛ 1⎞ 3 ⎛ 1⎞3⎜s+ ⎟ + ⎜s+ ⎟ +⎝ 2⎠ 4 ⎝ 2⎠4( ) =− + + 22 2H s3 3ht e t e t t e t t2 2−() 4 t −t () 2 −t=− σ + cos σ () + 2 2 sin σ ()Verificati expresia raspunsului la impuls folosind mediul Matlab:>> L=-1/(s+4)+(s+2)/(s^2+s+1)>> ilaplace(L)b) H( s)5s+ 7 5s+7= =3 2s + 5s + 5s+42( s+ 4)( s + s+1)b 1 =5, b 0 =7a 3 =1, a 2 =5, a 1 =5, a 0 =4sau: y′′′ + 5y′′ + 5y′ + 4y = 5x′+ 7x11