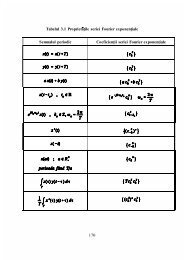
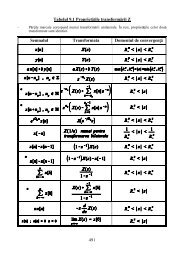
Esantionarea semnalelor

Eşantionarea semnalelor
Eşantionarea = prelevarea de probe dintr-un semnal la momente de timp decalate intre
ele cu T e – cu frecventa de eşantionare, f e =1/T e .
∞
xˆ t ∑ x kTe t k
e
k =−∞
() = ( ) δ ( − T )
Semnalul eşantionat ideal: .
Spectrul Xˆ
1
T
∞
∑
( ω) = X ( ω−kω
)
e k =−∞
e
Teorema eşantionării: Un semnal x(t) de energie finita si banda limitata B = ω
unic determinat de mulţimea eşantioanelor sale {x(nT e }|n∈Z} daca ωe
≥ 2ωM
.
Prin eşantionare cu perioada T e => ↔ ˆX ω . Semnalul original se poate
ˆx ( t ) ( )
reconstitui din spectrul semnalului eşantionat cu un FTJ cu frecventa de taiere ω
C
, astfel
încât, ω ≤ω ≤ω − ω => 2 ω ≤ ω sau f ≥ 2 f .
M C e M
M
e
e
M
M
este
-ω C +ωC
Caz limita: ωe
= 2ωM
, ωC = ωM
Caz defavorabil: ωe
< 2ωM
=> fenomenul de aliere, semnalul original nu poate fi
reconstituit.
sin ( ωCt
)
FTJ ideal: Hr( ω) = Tepω
( ω) ↔ h ( )
C
r
t = Te
πt
∞
2ω
sin ( ωC( t−
kTe)
)
C
Semnalul reconstituit: x () ˆ
r
t = x() t ∗ hr () t = ∑ x( kTe)
ω ω t−
kT
ωe
ωC
= ωM
= => Semnalul reconstituit:
2
r
k =−∞ e C
∞
∑
() = ( )
x t x kT
k =−∞
e
( )
⎛ ⎛ t ⎞⎞
sin
⎜
π ⎜ − k ⎟
T ⎟
⎝ ⎝ e ⎠⎠
⎛ t ⎞
π ⎜ − k ⎟
⎝Te
⎠
e
1

Probleme
1. Se considera sistemul din figura
x 1 (t)
( ) 2
y(t)
x 2 (t)
x 3 (t)
Suporturile transformatei Fourier ale semnalelor x i (t) i=1,3, sunt [-ω i , ω i ]. Determinaţi
perioada maxima de eşantionare T pentru care semnalul y(t) poate fi recuperat din
eşantioanele sale prin filtrare trece-jos ideala.
Rezolvare.
y () t 2
1
= x () t x () t () ( ) ( ) ( ) ( ) ( )
1 2
+ x t 3
↔ Y ω =
2 1 1 2 3
4
X ω ∗ X ω ∗ X ω +
π
X ω
sup X1( ω)
= −ω1, ω1 ⇒sup X1 ω ∗ X1 ω = − 2 ω1,2ω1
{ } [ ] { ( ) ( )} [ ]
{ X1( ω) ∗X1( ω) ∗ X2( ω)
} = [ − ω1− ω2 ω1+ω
2]
sup { Y ( ω)
} = ⎡− ωy, ω ⎤
y
, ωy
= max ( 2 ω1+
ω2,
ω3)
sup 2 ,2
=>
⎣ ⎦
Se aplica teorema eşantionării:
2π
π
ωe
≥ 2ω y
, cu perioada de eşantionare Te
= ≤
ω ω
Valoarea maxima pentru perioada de eşantionare este:
e
y
T e
π
=
max 2 ,
( ω + ω ω )
1 2 3
2. Se considera un sistem cu intrarea x(t) si ieşirea y(t) legate printr-o relaţie
polinomiala:
k
y = Px ( ) =∑ ax .
N
k = 0
k
Daca semnalul x(t) este de banda limitata la intervalul [-ω M , ω M ], determinaţi
perioada maxima de eşantionare pentru care semnalul y(t) poate fi recuperat din
eşantioanele sale prin filtrare trece-jos ideala.
Rezolvare.
Transformata Fourier a semnalului y(t) este:
a2
aN
Y( ω) = a + 0
a1X ( ω) + X ( ω) X ( ω)
... X ( ω) X ( ω) ... X
N
( )
2π
∗ + + 2π
∗ ∗ ∗ ω
( Y( ω)
) = [ − NωM
NωM]
=> sup ,
( )
de N ori
2

Teorema eşantionării: ω ≥ 2Nω
e
M
2π
π
=> ≥ 2NωM
=> T ≥ .
T
Nω
M
3. Se considera semnalul z(t) de banda limitata, la intervalul [ω , ω 1 2] cu spectrul din
figura:
1
Z(ω)
0
ω 1 ω 2
ω
ω2 + ω1
ω2 −ω1
Se notează ωC
= ; ωM
=
2
2
j Ct
a) arătaţi ca este valabila relaţia zt () = x t e ω , unde x 1 (t) este un semnal de banda
1
( )
limitata la intervalul [-ω M , ω M ].
b) utilizând formula de recuperare a semnalului x 1 (t) din eşantioanele sale,
determinaţi cea mai mare valoare T pentru care este valabila relaţia:
⎡ ⎛ t ⎞⎤
sin π n
∞
⎢ ⎜ − ⎟
j e ( t nT)
T
⎥
ω − ⎝ ⎠
z() t = z( nT)
e
⎣ ⎦
∑
n=−∞
⎛ t ⎞
π ⎜ − n⎟
⎝T
⎠
Rezolvare.
a) zt () = x j ωCt
t e ↔ Z ω = X ω−ω
1() ( ) 1( C )
1 ( ω) = Z( ω+
ωC
)
{ Z( )} = X1( −
C ) =
1
( ) = ω1 ω2
si
( ω − ω ) = − ω + ω ω +ω
X
spectrul X 1 deplasat la stânga cu ω fata de Z
sup ω sup { ω ω } [ ω , ω ]
{ Z ω } [ ]
{ X1
C } [ M C M C]
2
sup ,
sup ,
− ωM + ωC = ω1 si ωM + ωC
= ω2
(adevărat)
()
() j Ct
b) Semnalul x1 t = z t e − ω - banda limitata [-ωM, ω M ] => eşantionare cu ω ≥ 2ω
=> Semnalul recuperat
⎛ ⎛ t ⎞⎞
sin
π k
∞
⎜ ⎜ − ⎟
T ⎟
e
x1() t x1( kT
⎝ ⎝ ⎠⎠
ωe
= ∑ e )
daca ωC
= ωM
=
k =−∞
⎛ t ⎞
2
π ⎜ − k ⎟
⎝Te
⎠
C
e
M
3

∞
⎛ ⎛ t ⎞⎞
=> z() t = x1() t exp( jωCt) = ∑ exp( jωCt) x1( kTe)
sinc
π⎜
− k
⎜ ⎟
k =−∞
T ⎟
⎝ ⎝ e ⎠⎠
∞
⎛ ⎛ t ⎞⎞
=> z() t = ∑ exp( jωC( t−kTe)
) z( kTe)
sinc
π⎜
−k⎟
pt ω
⎜
k =−∞
T ⎟
C
⎝ ⎝ e ⎠⎠
ωe
= ωM
= , Te
2
π
=
ω
M
4. Semnalul z(t) al cărui spectru este reprezentat in figura, poate fi considerat ca semnalul
analitic asociat unui semnal real, x(t).
1
Z(ω)
0
ω 1 ω 2
ω
a) Reprezentaţi spectrul semnalului x(t).
b) Utilizând relaţia de legătura intre semnalele x(t), x t si z(t), unde x
t este
( )
()
transformata Hilbert a semnalului x(t), determinaţi cea mai mare valoare T pentru care
sunt adevărate relaţiile:
( ) { ( ) ( ) ( ) ( ) } sin ⎡ ⎛ t ⎞⎤
π n
∞
⎢ ⎜ − ⎟
T
⎥
⎝ ⎠
x t = x nT cos ωC
t nT x nT sin ωC
t nT
⎣ ⎦
∑ ⎡⎣ − ⎤⎦− ⎡⎣ − ⎤⎦
n=−∞
⎛ t ⎞
π ⎜ − n⎟
⎝T
⎠
∞
∑
{ } sin
⎡
C
⎤ ⎡
C
⎤
( ) = ( ) cos ω ( − ) + ( ) sin ω ( − )
x t x nT ⎣ t nT ⎦ x
nT ⎣ t nT ⎦
n=−∞
⎡ ⎛ t ⎞⎤
⎢π
⎜ − n⎟
T
⎥
⎣ ⎝ ⎠⎦
⎛ t ⎞
π ⎜ − n⎟
⎝T
⎠
c) Pe baza relaţiilor anterioare, in figura următoare sunt reprezentate schemele unor
sisteme care permit ca din semnalele eşantionate xe( t) = x( t) δT
( t)
si xe() t = x() t δT
( t)
sa se recupereze semnalele x()
t si x
( t)
. Determinaţi răspunsul la impuls h 1 (t) si h 2 (t) si
răspunsurile in frecventa H (ω) si H (ω) ale sistemelor corespunzătoare.
1 2
4

x e (t)
x
e
() t
h 1 (t)
h 2 (t)
x e (t)
h 1 (t)
x(t) x
() t
x
e
( t)
h 2 (t)
Rezolvare.
1
a) x(t) = Re(z(t)), xt () = H( xt ()) = ∗xt ( ) ↔ X
( ω) =−jsgnωX
( ω)
πt
z() t = x() t + jx
() t
Z( ω) = X ( ω) + jX
( ω) = X ( ω) + j( − jsgnω) X ( ω) = X ( ω) + sgnωX ( ω)
Z
⎧ 2 X ( ω)
, ω > 0
Z ( −ω
)
( ω)
= ⎨ => ω < 0: X ( − ω)
= , ω 0: X ( ω)
⎩
0, in rest
2
( ω)
Z
> =
2
X(ω)
1/2
ω
-ω 2
-ω 1
0
ω 1 ω 2
b) Trebuie demonstrata relaţia:
∞
∑ ∑ −
( ) = ( ) ( − ) − ( ) (
x t x nT h t nT x nT h t nT
n=−∞
π
h () t = cosω
tsinc
t ↔ H
T
π
h () t = sinω
tsinc
t ↔ H
T
1 C
1
2 C
2
sincω0t p ω 0
ω0
1 2
n=−∞
π
↔ ( ω)
=> pt.
0
∞
π
T
1
H1
Tp π
C
2π
⎣
T
1
H1
ω = T ⎡pπ
ω− ωC
+ pπ
ω+
ω
C
2 ⎢⎣
T
T
π
T
ω = , sinc t ↔ Tp ( ω)
( ω) = ( ω) ∗π ⎡δ ( ω− ω ) + δ ( ω+
ω )
( ) ( ) ( )
⎤
⎥⎦
C
)
⎤⎦
π
T
5

1 π
H2
( ω) = Tpπ ( ω) ∗ ⎡δ ( ω−ωC) − δ ( ω+
C)
⎤
2π
T j
⎣
ω ⎦
1
H2
( ω) = T ⎡pπ
( ω−ωC) − pπ
( ω+
ω
C)
⎤
2 j ⎢⎣
T
T ⎥⎦
T/2
H 1 (ω)
0
-ω C -π/T -ω C -ω C +π/T ω C -π/T ω C
ω
ω C +π/T
T/2
jH 2 (ω)
-ω C
0
ω C -π/T ω C
ω
ω C +π/T
T
T
=> X H1
X si
2 2
ω
2
2
( ω) ( ω) = ( ω)
jX
( ω) jH ( ω) = sgnωX ( ω) jH ( ω) = X ( )
=>
T
X
H2
X
2
( ω) ( ω) =− ( ω)
( ω) ( ω) − ( ω) ( ω) = ( ω )
X H X H TX
1 2
Eşantionarea semnalelor x si x :
e
() = ∑ ( ) δ ( − ) ↔ Xe
( ω)
x t x nT t nT
x () t = x( nT) δ ( t−nT)
↔ X ( ω)
e
∑
∞
1 ⎛ 2
X k π ⎞
= ∑ ⎜ω−
⎟
T k =−∞ ⎝ T ⎠
∞
1 ⎛ 2
e
X ω k π ⎞
= ∑
⎜ − ⎟
T k =−∞ ⎝ T ⎠
6

e
( ω) =− sgnω ( ω)
X
j X
e
π
π π ω2 −ω1
Pentru refacerea semnalului x(t) din x e(t): ωC
− < ω1 < ω2
< ωC
+ => >
T
T T 2
1 T 1
Xe
( ω) H1
( ω) = X ( ω) = X ( ω )
T 2 2
1
X
e
H2
X
2
( ω) ( ω) =− ( ω)
De aceea,
e
( ω) ( ω) − ( ω) ( ω) = ( ω )
X H X H X
1 e 2
In domeniul timp:
⎛π
x t x nT t nT x nT t nT t nT
⎝
∞
= ∑ ⎣ ⎣ C
− ⎦−
⎣ C
− ⎦⎦
⎜ − ⎟
k =−∞
T
( ) ⎡ ( ) cos ⎡ω
( ) ⎤ ( ) sin ⎡ω
( ) ⎤⎤sinc
( )
Pentru a doua relaţie:
− jsgnωX ( ω) H ( ω) =− jsgnωX
( ω)
=> X
( ω) H ( ω) = X
( ω)
e
1
1
2
1
jsgnω Xe
ω H2
ω j ωX
2
( ) ( ) =− sgn ( ω ) => X ( ω) H ( ω) = X
( ω)
e
e
2
1
1
2
1
2
⎞
⎠
De aceea,
e
( ω) ( ω) + ( ω) ( ω) = ( ω )
X H X H X
2 e 1
In domeniul timp:
⎛π
x t x nT t nT x nT t nT t − nT
⎝
∞
= ∑ ⎣ ⎣ C
− ⎦+ ⎣ C
− ⎦⎦
⎜ ⎟
k =−∞
T
( ) ⎡ ( ) cos ⎡ω
( ) ⎤ ( ) sin ⎡ω
( ) ⎤⎤sinc
( )
5. Se considera semnalul x(t) având spectrul concentrat ca in figura:
⎞
⎠
1
X(ω)
ω
-ω 2
-ω 1
0
ω 1 ω 2
Se păstrează relaţiile ca in problema 3. Se eşantionează ideal semnalul cu frecventa
2ω M
π .
7

a) reprezentaţi spectrul semnalului eşantionat in ipoteza (4k+3)ω M = ω C
b) (4k+1)ω M=ωC
c) reprezentaţi schemele unor sisteme care sa permită recuperarea semnalului x(t) din
semnalele eşantionate obţinute la punctele anterioare.
Rezolvare.
a) Pulsaţia de eşantionare: ω = 2π2ω π = 4ω
X
e
( ω)
∞
1 ⎛ 2
X k π ⎞
= ∑ ⎜ω−
⎟
T k =−∞ ⎝ T ⎠
e M M
(4k+3)ω M = ω C => k=1, ω C = 7ωM, ω 1 = 6ωM, ω 2 = 8ωM
1/T
X e (ω)
…
…
-ω 2 -ω 1
0
ω 1 ω 2
ω
b) (4k+1)ω M = ω C => k=1, ω C = 5ω M, ω 1 = 4ωM, ω 2 = 6ωM
1/T
X e (ω)
…
…
-ω 2 -ω 1 0
ω 1 ω 2
ω
c) Reconstrucţia: filtre trece-banda
2ω M /π
H r (ω)
0
-8ω M -6ω M -4ω M M 6ω M
84ω
8ω M
ω

6. Se considera sistemul din figura. x(t) este un semnal de banda limitata la intervalul
[-ω M , ω M ], iar p(t) este un semnal periodic de perioada T = π ω .
M
x(t)
p(t)
x e (t)
a) notând cu X(ω) spectrul semnalului x(t) si cu a n
coeficienţii dezvoltării Fourier a semnalului p(t), aratati ca
spectrul semnalului eşantionat se poate scrie:
∞
∑ n
e
, ω e=
n=−∞
( ω) = ( ω−
ω )
X a X n
e
b) presupunând ca x(t) are o componenta continua nenula
a0 ≠ 0, aratati ca x(t) se poate recupera din x e (t) prin filtrare trece-jos ideala si
determinaţi parametrii filtrului trece-jos.
c) imaginaţi un sistem nu neapărat liniar si invariant in timp, care sa permită recuperarea
semnalului x(t) din x e (t) in cazul a 0 =0.
d) daca x(t) are spectrul din figura reprezentaţi modulul spectrului semnalului x e (t) in
următoarele cazuri p(t)=δ T (t); p(t)=δ T (t-Δ).
X(ω)
∞
a) p()
t = ∑ ane
n=−∞
2π
jn t
T
∞
1
⎛ 2
P( ω)
2πanδ ω n π ⎞
= ∑ ⎜ − ⎟
n=−∞
⎝ T ⎠
-ω M
0
ω M
ω
1
Xe
( ω) = X ( ω) ∗ P( ω)
2π
2π
Xe( ω)
= anX ⎜ω−n ⎞
⎟
n ⎝ T ⎠
2π
ωe
= = 2ωM
T
⎛ 2π
⎞
b) a0 ≠ 0 => Xe( ω) = a0
X ( ω)
+ ∑ anX ⎜ω−n ⎟
n≠0
⎝ T ⎠
H(ω)
1/a 0
ω
⎛ 2π
⎞
= 0, ≠ 0 => Xe( ω) = a1
X ( ω)
+ ∑ anX ⎜ω−n ⎟
n≠0,1
⎝ T ⎠
c) a0 a1
-ω M ω M
0
9

H 1 (ω)
1/a 1
ω
x e (t)
h 1 (t)
x(t)
2ω M
2π/T-ω M 2π/T+ω M
=ω M =3ω M
exp(-j2πt/T)
d) p(t)=δ T (t);
P
2π
T
( ω) = δ ( ω)
2π
T
1 1 ⎛ 2π ⎞
Xe
( ω) = X ( ω) ∗ P( ω)
= ∑ X ⎜ω−k
⎟
2π
T ⎝ T ⎠
…
X(ω)
1/T
…
0
-ω M ω M
2ω M
ω
p(t)=δ T (t-Δ);
P
2π
T
− jωΔ
( ω) = e δ ( ω)
2π
T
1 1 − jωΔ 2π
⎛ 2π
⎞
Xe
( ω) = X ( ω) ∗ P( ω) = X ( ω) ∗e ∑ δ2π
⎜ω−k
⎟
2π
2π
T k ⎝ T ⎠
T
2π
2π
− jk Δ π − jk Δ
T
T
1 ⎛ 2π
⎞ 1 ⎛ 2 ⎞
Xe
( ω) = X ( ω)
∗∑δ ⎜ω− k ⎟e = ∑X ⎜ω−k ⎟e
T k ⎝ T ⎠ T k ⎝ T ⎠
1 2π
Xe
( ω)
= ∑ X ⎛
⎜ω−k
⎞
⎟
T k ⎝ T ⎠
10