Livro Hibbeler - 7ª ed Resistencia Materiais (Livro)
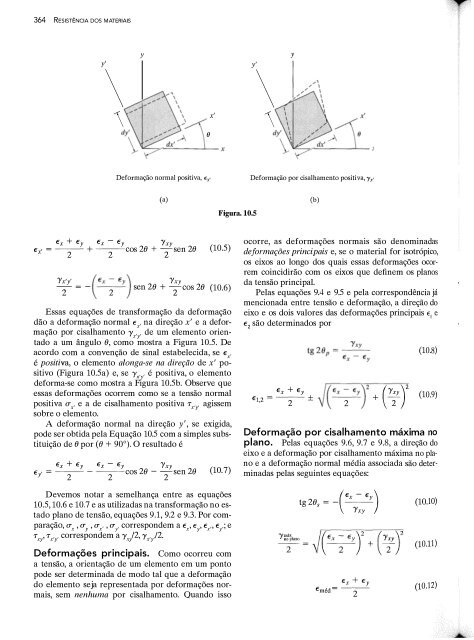
364 RESISTÊNCIA DOS MATERIAIS y' \ \ y y' y \ {) x ' \ Deformação normal positiva, Ex• Deformação por cisalhamento positiva, 'Yx' (a) Figura. 10.5 (b) Ex + Ey Ex - Ey 'Yxy Ex' = + 2 2 c os 28 + 2 sen 28 (10.5) 'Yx'y' ( E x - Ey) 'Yxy 2 = - 2 sen 28 + 2 cos 28 (10.6) Essas equações de transformação da deformação dão a deformação normal Ex, na direção x ' e a deformação por cisalhamento 'Yx'y' de um elemento orientado a um ângulo 8, como mostra a Figura 10.5. De acordo com a convenção de sinal estabelecida, se E , é positiva, o elemento alonga-se na direção de x ' po " sitivo (Figura 10.5a) e, se y , . é positiva, o elemento x y deforma-se como mostra a Figura 10.5b. Observe que essas deformações ocorrem como se a tensão normal positiva rrx' e a de cisalhamento positiva rx'y ' agissem sobre o elemento. A deformação normal na direção y ' , se exigida, pode ser obtida pela Equação 10.5 com a simples substituição de 8 por (8 + 90°). O resultado é Ex + Ey Ex - Ey Ey• = --- - cos 28 - -sen 28 'Yxy 2 2 2 (10.7) Devemos notar a semelhança entre as equações 10.5, 10.6 e 10.7 e as utilizadas na transformação no estado plano de tensão, equações 9.1, 9.2 e 9.3. Por comparação, rr x , rr y , rr x , , rr }.. correspondem a E x, E y, E x .., E,.; ) e rxy' rx' y ' correspondem a 'Y. q /2, 'Yx•y ,/2. Deformações principais. Como ocorreu com a tensão, a orientação de um elemento em um ponto pode ser determinada de modo tal que a deformação do elemento seja representada por deformações normais, sem nenhuma por cisalhamento. Quando isso ocorre, as deformações normais são denominadas deformações principais e, se o material for isotrópico, os eixos ao longo dos quais essas deformações ocorrem coincidirão com os eixos que definem os planos da tensão principal. Pelas equações 9.4 e 9.5 e pela correspondência já mencionada entre tensão e deformação, a direção do eixo e os dois valores das deformações principais E 1 e E2 são determinados por E1,2 - _ Ex (10.8) + Ey f( E x - Ey)z ('Yxy)z (10.9) 2 ± \j 2 Deformação por cisalhamento máxima no plano. Pelas equações 9.6, 9.7 e 9.8, a direção do eixo e a deformação por cisalhamento máxima no pia· no e a deformação normal média associada são deter· minadas pelas seguintes equações: + tg 28s = - (E x - Ey) 'Yxy Eméd= 2 2 (10.10) (10.11) (10.12)
TRANSFORMAÇÃO DA DEFORMAÇÃO 365 de defon#ação é .r't epr,seí:ltatlto pêláis ,d
- Page 330 and 331: 314 RESISTÊNCIA DOS MATERIAIS 8.37
- Page 332 and 333: 316 RESISTÊNCIA DOS MATERIAIS D 8.
- Page 334 and 335: 318 RESISTÊNCIA DOS MATERIAIS A su
- Page 336 and 337: 320 RESISTÊNCIA DOS MATERIAIS 40 k
- Page 338 and 339: 322 RESISTtNCIA DOS MATERIAIS y I x
- Page 340 and 341: 324 RESISTNCIA DOS MATERIAIS +'\2:F
- Page 342 and 343: 326 RESISTtoNCIA DOS MATERIAIS Para
- Page 344 and 345: 328 RESISTNCIA DOS MATERIAIS da tom
- Page 346 and 347: 330 RESISTÊNCIA DOS MATERIAIS ··
- Page 348 and 349: 332 RESISTtNCIA DOS MATERIAIS Assim
- Page 350 and 351: 334 RESISTÊNCIA DOS MATERIAIS --r
- Page 352 and 353: 336 RESISTNCIA DOS MATERIAIS p Prob
- Page 354 and 355: 338 RESISTÊNCIA DOS MATERIAIS 9.4
- Page 356 and 357: 340 RESISTÊNCIA DOS MATERIAIS As s
- Page 358 and 359: 342 RESISTÊNCIA DOS MATERIAIS p p
- Page 360 and 361: 344 RESISTÊNCIA DOS MATERIAIS 90 M
- Page 362 and 363: 346 RESISTNCIA DOS MATERIAIS N·m p
- Page 364 and 365: 348 RESISTÊNCIA DOS MATERIAIS Tens
- Page 366 and 367: 350 RESISTÊNCIA DOS MATERIAIS 9. 7
- Page 368 and 369: 352 RESISTÊNCIA DOS MATERIAIS da t
- Page 370 and 371: 354 RESISTÊNCIA DOS MATERIAIS z '
- Page 372 and 373: 356 RESISTÊNCIA DOS MATERIAIS Figu
- Page 374 and 375: 358 RESISTti\ICIA DOS MATERIAIS A t
- Page 376 and 377: 360 RESISTÊNCIA DOS MATERIAIS 9.98
- Page 378 and 379: 362 RESISTÊNCIA DOS MATERIAIS z +'
- Page 382 and 383: 366 RESISTÊNCIA DOS MATERIAIS 200(
- Page 384 and 385: '. . . ':?'( 368 RESISTÊNCIA DOS M
- Page 386 and 387: 370 RESISTÊNCIA DOS MATERIAIS · F
- Page 388 and 389: 372 RESISTÊNCIA DOS MATERIAIS *10.
- Page 390 and 391: 3 7 4 RESISTÊNCIA DOS MATERIAIS di
- Page 392 and 393: 37 6 RESISTÊNCIA DOS MATERIAIS ·
- Page 394 and 395: • 378 RESISTÊNCIA DOS MATERIAIS
- Page 396 and 397: 380 RESISTNCIA DOS MATERIAIS + (a)
- Page 398 and 399: .. 382 RESISTÊNCIA DOS MATERIAIS d
- Page 400 and 401: 384 RESISTÊNCIA DOS MATERIAIS SOLU
- Page 402 and 403: 386 RESISTNCIA DOS MATERIAIS *10.52
- Page 404 and 405: 388 RESISTÊNCIA DOS MATERIAIS rial
- Page 406 and 407: 390 RESISTÊNCIA DOS MATERIAIS prin
- Page 408 and 409: 392 RESISTtNCIA DOS MATERIAIS (J 2
- Page 410 and 411: 394 RESISTl:NCIA DOS MATERIAIS O po
- Page 412 and 413: 396 RESISTtNCIA DOS MATERIAIS máxi
- Page 414 and 415: ... .. 398 RESISTÊNCIA DOS MATERIA
- Page 416 and 417: 400 RESISTNCIA DOS MATERIAIS 0 "'
- Page 418 and 419: 402 RESISTNCIA DOS MATERIAIS jeto p
- Page 420 and 421: 404 RESISTÊNCIA DOS MATERIAIS Tens
- Page 422 and 423: 406 RESISTÊNCIA DOS MATERIAIS Q =
- Page 424 and 425: 408 RESISTÊNCIA DOS MATERIAIS 11.7
- Page 426 and 427: 41 0 RESISTÊNCIA DOS MATERIAIS ter
- Page 428 and 429: 412 RESISTÊNCIA DOS MATERIAIS reta
364 RESISTÊNCIA DOS MATERIAIS<br />
y'<br />
\ \<br />
y<br />
y'<br />
y<br />
\<br />
{)<br />
x ' \<br />
Deformação normal positiva, Ex•<br />
Deformação por cisalhamento positiva, 'Yx'<br />
(a)<br />
Figura. 10.5<br />
(b)<br />
Ex + Ey Ex - Ey 'Yxy<br />
Ex' = +<br />
2 2<br />
c os 28 + 2 sen 28 (10.5)<br />
'Yx'y' ( E x - Ey) 'Yxy<br />
2 = -<br />
2<br />
sen 28 + 2<br />
cos 28 (10.6)<br />
Essas equações de transformação da deformação<br />
dão a deformação normal Ex, na direção x ' e a deformação<br />
por cisalhamento 'Yx'y' de um elemento orientado<br />
a um ângulo 8, como mostra a Figura 10.5. De<br />
acordo com a convenção de sinal estabelecida, se E ,<br />
é positiva, o elemento alonga-se na direção de x ' po " <br />
sitivo (Figura 10.5a) e, se y , . é positiva, o elemento<br />
x y<br />
deforma-se como mostra a Figura 10.5b. Observe que<br />
essas deformações ocorrem como se a tensão normal<br />
positiva rrx' e a de cisalhamento positiva rx'y ' agissem<br />
sobre o elemento.<br />
A deformação normal na direção y ' , se exigida,<br />
pode ser obtida pela Equação 10.5 com a simples substituição<br />
de 8 por (8 + 90°). O resultado é<br />
Ex + Ey Ex - Ey<br />
Ey• = --- - cos 28 - -sen 28<br />
'Yxy<br />
2 2 2<br />
(10.7)<br />
Devemos notar a semelhança entre as equações<br />
10.5, 10.6 e 10.7 e as utilizadas na transformação no estado<br />
plano de tensão, equações 9.1, 9.2 e 9.3. Por comparação,<br />
rr x , rr y , rr x , , rr }.. correspondem a E x, E y, E x .., E,.; ) e<br />
rxy' rx' y ' correspondem a 'Y. q<br />
/2, 'Yx•y ,/2.<br />
Deformações principais. Como ocorreu com<br />
a tensão, a orientação de um elemento em um ponto<br />
pode ser determinada de modo tal que a deformação<br />
do elemento seja representada por deformações normais,<br />
sem nenhuma por cisalhamento. Quando isso<br />
ocorre, as deformações normais são denominadas<br />
deformações principais e, se o material for isotrópico,<br />
os eixos ao longo dos quais essas deformações ocorrem<br />
coincidirão com os eixos que definem os planos<br />
da tensão principal.<br />
Pelas equações 9.4 e 9.5 e pela correspondência já<br />
mencionada entre tensão e deformação, a direção do<br />
eixo e os dois valores das deformações principais E 1<br />
e<br />
E2 são determinados por<br />
E1,2 -<br />
_ Ex<br />
(10.8)<br />
+ Ey f( E x - Ey)z ('Yxy)z (10.9)<br />
2 ± \j 2<br />
Deformação por cisalhamento máxima no<br />
plano.<br />
Pelas equações 9.6, 9.7 e 9.8, a direção do<br />
eixo e a deformação por cisalhamento máxima no pia·<br />
no e a deformação normal média associada são deter·<br />
minadas pelas seguintes equações:<br />
+<br />
tg 28s = - (E x - Ey)<br />
'Yxy<br />
Eméd=<br />
2<br />
2<br />
(10.10)<br />
(10.11)<br />
(10.12)