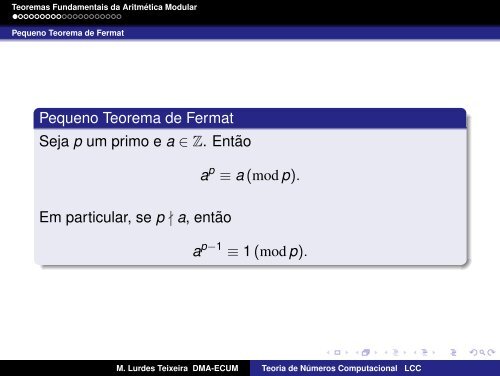
Pequeno Teorema de Fermat Seja p um primo e a ∈ Z. Ent˜ao ap ...

Teoremas Fundamentais da Aritmética Modular 

Pequeno Teorema de Fermat 


Seja p um primo e a ∈ Z. Então 

a p ≡ a (mod p). 

Em particular, se p ∤ a, então 

a p−1 ≡ 1 (mod p). 

M. Lurdes Teixeira DMA-ECUM Teoria de Números Computacional LCC



Demonstração (efectuada por Euler em 1730) : 

p = 2 a 2 ≡ a (mod 2) ⇔ 2 | a(a − 1) e a(a − 1) é par. 

p > 2 Para a = 0 e a = 1 a afirmação é verdadeira. 

Por hipótese de indução, suponhamos que, para 

certo a ∈ N 0 , a p ≡ a (mod p). 

Então, 

(a + 1) p ≡a p + ( p 1 )ap−1 + · · · + ( p 

p−1 

)a + 1 (mod p) 

≡a p + 1 (mod p) 

≡a + 1 (mod p) 

Logo a p ≡ a (mod p), para todo a ∈ N 0 . 

Como p − 1 é par, então a p−1 = (−a) p−1 pelo que a afirmação 

é válida para todo o a ∈ Z. 




Exemplo 

2 50 + 3 50 é divisível por 13. 

2 50 =2 4·12+2 = (2 12 ) 4 · 2 2 logo 

2 50 ≡2 2 (mod 13) 

3 50 =3 4·12+2 = (3 12 ) 4 · 3 2 logo 

3 50 ≡3 2 (mod 13) 

2 50 + 3 50 ≡2 2 + 3 2 (mod 13) 

≡0 (mod 13) 




Exercícios 

1 Calcule o resto da divisão de 3 372 por 37. 

2 Mostre que 7 ∤ n 2 + 1 qualquer que seja n ∈ Z. 

3 Calcule 

31 100 mod 19, 

2 10000 mod 29. 

4 Mostre que 11 84 − 5 84 é divisível por 7. 

5 Mostre que, para qualquer n ∈ N, 

1 se n ≡ 2 (mod 4), então 5 | 9 n + 8 n ; 

2 n 13 − n ≡ 0 (mod 2730). 

6 Mostre que para qualquer primo p > 3, ab p − ba p é 

divisível por 6p, para quaisquer inteiros a e b. 




Será o recíproco do Teorema de Fermat válido 

i.e., se a n−1 ≡ 1 (mod n) para todo o inteiro a tal que 

m.d.c.(a, n) = 1, então n é primo 

Não, por exemplo, 561 é tal que: 

561 = 3 · 11 · 17 

a 560 ≡ 1 (mod 561), para qualquer a ∈ Z tal que 

m.d.c.(a, 561) = 1. 




Definição 

Seja a ∈ Z. Um inteiro composto n tal que 

a n−1 ≡ 1 (mod n) 

diz-se um pseudoprimo de base a. 

Se n é pseudoprimo de base a para todo o inteiro a tal que 

m.d.c.(a, n) = 1, então n diz-se um pseudoprimo, ou um 

número de Carmichael. 

Exemplos 

São pseudoprimos os números: 561, 1105, 1729, 2465, 2821, 

6601, . . . 

São pseudoprimos de base 2 os números: 341, 561, 645, 

1105, 1387, 1729, 1905, . . . 




Se n é um primo que não divide a(a 2 − 1), então a2n −1 

a 2 −1 é um 

pseudoprimo de base a. 

Logo existe uma infinidade de pseudoprimos de base a para 

qualquer a. 

Teorema (Alford, Granville, Pomerance-1994) 

Há uma infinidade de números pseudoprimos. 

Demonstração: 

Se n é um pseudoprimo então 2 n − 1 também é. 




Proposição 

Suponhamos que a r ≡ 1 (mod p) com p primo. Se 

m.d.c.(r, p − 1) = d, então 

Exemplo 

a d ≡ 1 (mod p). 

Há uma infinidade de primos do tipo 8k + 1. 

Se os primos do tipo 8k + 1 fossem em número finito, então 

poder-se -ia admitir que existe l tal que {p 1 , . . . , p l } é o 

conjunto de todos os primos da forma 8k + 1. 

Seja N = (2p 1 · · · p l ) 4 + 1. Então, 

1 N > p i para 1 ≤ i ≤ l; 

2 N é do tipo 8k + 1; 

3 N é primo. 




Exercícios 

1 Mostre que: 

91 é um pseudoprimo de base 3; 

45 é um pseudoprimo de base 17; 

45 é um pseudoprimo de base 19. 

2 Mostre que se n é um pseudoprimo de base a e de base 

b, então n é um pseudoprimo de base ab. 

3 Seja p > 2 um primo. On números da forma 2 p − 1 são 

designados números de Mersenne. Mostre que se q é um 

primo que divide 2 p − 1, então q = 2kp + 1 para algum 

k ∈ Z. 

4 Os números da forma F n = 2 2n + 1, com n ≥ 0, designam- 

-se números de Fermat. Mostre que os inteiros n que são 

números de Mersenne ou números de Fermat verificam 

2 n−1 ≡ 1 (mod n). 



Teorema de Euler 

Definição 

O número de elementos invertíveis módulo n num sistema 

completo de resíduos denota-se por φ(n). A função 

chama-se função φ de Euler. 

Exemplos 

φ : N → N 

n ↦→ φ(n) 

φ(2) = 1, φ(3) = 2, φ(4) = 2, φ(5) = 4, φ(6) = 2. 

φ(p) = p − 1 se p é primo. 

Exercício 

Mostre que se p é primo, então φ(p r ) = p r−1 (p − 1), para r ≥ 1. 




Teorema 

Se m e n são inteiros tais que m.d.c.(m, n) = 1, então 

φ(mn) = φ(m)φ(n), 

i.e., φ é multiplicativa. 

Exemplo 

φ(6600) = φ(11 · 5 2 · 3 · 2 3 ) = 10 · (5 · 4) · 2 · (2 2 · 1) = 1600 




Exercícios 

1 Prove que existe uma infinidade de números primos 

usando a função φ. 

2 Escreva uma função no Mathematica que calcule φ(n), 

para n ∈ N. 

3 Teste a função definida no exercício anterior calculando 

φ(120) e φ(225). 

4 Determine os valores de n para os quais φ(n) = 6. 

5 Determine os valores de n para os quais φ(n) = n − 2. 





Se a e m são inteiros tais que m.d.c.(a, m) = 1, então 

a φ(m) ≡ 1 (mod m). 


Se r 1 , . . . , r φ(m) são os elementos invertíveis módulo m num 

sistema completo de resíduos, então 

ar 1 , . . . , ar φ(m) 

são invertíveis e incongruentes dois a dois módulo m. 

ar 1 · · · ar φ(m) = a φ(m) (r 1 · · · r φ(m) ) ≡ r 1 · · · r φ(m) (mod m). 

Como m.d.c.(r i , m) = 1, então 

a φ(m) ≡ 1 (mod m). 




Exemplo 

Calcular os últimos dois dígitos de 1993 1993 . 

} 

φ(100) = 40 

→ 1993 40 ≡ 1 (mod 100) 

m.d.c.(1993, 100) = 1 

Dado que 1993 mod 40 = 33, 

1993 1993 ≡ 1993 33 (mod 100) 

≡ 93 33 (mod 100) 

≡ −7 33 (mod 100) 

≡ −(7 4 ) 8 7 (mod 100) 

≡ −7 (mod 100) ( porque 7 4 ≡ 1 (mod 100)) 

≡ 93 (mod 100) 




Exemplo 

Calcular inverso de a módulo m. 

Se m.d.c.(a, m) ≠ 1, então a não é invertível módulo m. 

Senão, 

a φ(m) ≡ 1 (mod m), 

ou seja, 

a · a φ(m)−1 ≡ 1 (mod m). 




Exercícios 

1 Calcule o inverso de 2 e de 3 módulo 35. 

2 Calcule o resto da divisão de 2 720 por 225. 

3 Calcule: 

3 340 mod 341; 

7 89 mod 100; 

2 10000 mod 121. 

4 Mostre que n 12 ≡ 1 (mod 72) para qualquer inteiro n tal 

que m.d.c.(n, 72) = 1. 

5 Verifique que se p é primo, então 

1 p−1 + 2 p−1 + · · · + (p − 1) p−1 ≡ −1 mod p). 

6 Escreva um a função que permita verificar para que 

inteiros a congruência da questão anterior é válida. 



Teorema de Lagrange 

Teorema de Lagrange 

Se K é um corpo e f (x) é uma função polinomial de grau n em 

K[x], então a equação f (x) = 0 tem no máximo n soluções. 

Corolário 

Se p é um primo e f (x) é uma função polinomial de grau n de 

coeficientes inteiros em que nem todos são divisíveis por p, 

então a congruência f (x) ≡ 0 (mod p) tem no máximo n soluções 

módulo p. 

Corolário 

Se p é um primo e d | p − 1, então a congruência 

x d − 1 ≡ 0 (mod p) 

tem exactamente d soluções módulo p. 



Teorema de Wilson 


Se p é primo, então 


(p − 1)! ≡ −1 (mod p). 

S = {0, 1, 2, . . . , p − 1} 

é um sistema completo de resíduos. 

Logo, 

1 e p − 1 são inversos módulo p de si próprios; 

os restantes elementos não nulos podem agrupar-se em 

pares de elementos distintos do tipo (a, a ′ ) em que a é 

inverso módulo p de a ′ . 

1 · 2 · · · · · (p − 1) ≡ 1 · (p − 1) (mod p) 

≡ (p − 1) (mod p) 




O recíproco do Teorema de Wilson também é válido: 

Se (p − 1)! ≡ −1 (mod p), então p é primo. 

Proposição 

Se n é um composto e n > 1, então 

{ 2 mod n se n = 4 

(n − 1)! ≡ 

0 mod n se n ≠ 4 . 




Exercícios 

1 Calcule o resto da divisão de 

87! por 89; 

18! por 437; 

13! 

7! 

por 7. 

2 Mostre que se p é um primo ímpar, então 

2(p − 3)! ≡ −1 (mod p).

Pequeno Teorema de Fermat Seja p um primo e a ∈ Z. Ent˜ao ap ...

Create successful ePaper yourself

Delete template?

Save as template?