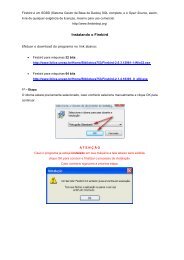
Curso de Equações Diferenciais Ordinárias - Unesp

Curso de Equações Diferenciais Ordinárias
1 Introdução
——
Definição: Uma equação diferencial é uma equação onde aparece uma ou
mais derivadas de uma função desconhecida.
Exemplos:
1)
t : tempo
x (t) : posição
.
x (t) : velocidade
..
x (t) : aceleração
F ( t, x, ẋ) = m .ẋ
2)
Observe que
y ′′ + y ′ = 0
y 1 (x) = c, constante
y 2 (x) = e −x
são soluções.
OBJETIVOS:
-Encontrar as soluções (Análise).
-Propriedades das soluções (Geometria e Topologia: Sistemas Dinâmicos).
-Métodos Numéricos ( Matemática Aplicada).
O Teorema Fundamental do Cálculo
Se
f : [a, b] → R
é uma função contínua então a função dada por
F (x) =
∫ x
a
f (t) dt
1

é derivável e
F ′ (x) = f (x) .
Prova:
Observe que o teorema está afirmando que F (x) é a solução do PVI (Problema
de Valor Inicial) { y ′ (x) = f (x)
.
y (a) = 0
Para provarmos o teorema basta calcularmos F ′ (x) :
F ′ F (x + h) − F (x)
(x) = lim
=
h→0 h
∫ x+h
x
h→0
= lim
f (t) dt
h
f (c h ) h
= lim = ∗
h→0 h
onde c h é um número entre x e x + h, conforme o Teorema do Valor Médio
Integral. Assim a continuidade de f nos garante que
∗ = f (x) .
Classificação das Equações Diferenciais:
-Quanto ao tipo: Chamamos de EDO (Equações Diferenciais Ordinárias)
aquelas onde aparecem apenas as derivadas ordinárias e chamamos de EDP
(Equações Diferenciais Parciais) aquelas onde aparecem derivadas parciais.
-Quanto a ordem: A ordem de uma equação diferencial é a ordem da maior
derivada que aparece na equação.
Exemplos:
1)
é uma EDO de 1 a ordem.
2)
é uma EDP de 2 a ordem.
y ′ + y = sin x
u t = u xx
OBSERVAÇÃO: A Forma Geral das EDO’s que iremos estudar neste
curso é
(
y (n) = f t, y, y ′ , ..., y (n−1)) .
QUESTÕES QUE ABORDAREMOS:
-Sempre têm soluções (Existência)
-Quantas soluções (Unicidade)
-É possível determiná-las 2

2 Equações Diferenciais Ordinárias de Primeira
Ordem
Uma EDO de primeira ordem é uma equação da forma
y ′ = f (t, y)
Uma solução para a equação acima é uma função
φ : I → R
onde I ⊂ R é um intervalo aberto e φ satisfaz
φ ′ (t) = f (t, φ (t)) , ∀t ∈ I.
Um PVI de primeira ordem é uma equação de primeira ordem acompanhada
de uma condição, chamada de condição inicial
{ y ′ = f (t, y)
y (t 0 ) = y 0
.
Uma solução do PVI é uma função φ como acima, satisfazendo ainda que
a)
t 0 ∈ I
b)
φ (t 0 ) = y 0 .
INTERPRETAÇÃO GEOMÉTRICA DAS EDO’S DE PRIMEIRA
ORDEM
Dada a EDO
temos que uma solução é uma curva
que tem como vetor tangente
Considere por exemplo a EDO
y ′ = f(t, y)
(t, y (t))
(1, f (t, y)) .
y ′ = 3 − y
2
Com o auxílio do MAPLE podemos ”plotar” o campo de vetores
(
1, 3 − y )
2
e termos uma idéia do comportamento das soluções:
3

2.1 EDO’s Lineares de Primeira Ordem
Uma EDO linear de primeira ordem é uma equação do tipo
Se
y ′ + p (t) y = g (t) .
g ≡ 0
então a equação é dita HOMOGÊNEA.
Exemplos:
1)
É óbvio que
y ′ + y 2 = 3 2
y = 3
é uma solução. Vejamos como podem ser as outras.
Temos
dy
dt = 3 − y
2
e assim
se
1 dy
3 − y dt = 1 2
y ≠ 3.
Então
d
dt (ln |y − 3|) = −1 2
Segue que qualquer solução da equação deverá ser da forma
onde k é uma constante real.
Observe que se k > 0 então
e se k < 0 então
y = ke − t 2 + 3
lim t→+∞ = 3
lim t→−∞ = +∞
lim t→+∞ = 3
lim t→−∞ = −∞
4

2) Da mesma forma como no anterior temos que as soluções de
dy
dt
= ry + k,
onde r ≠ 0 e k são constantes reais, são dadas por
onde M é uma constante real.
3) Vamos resolver o PVI
y = Me rt − k r
{ y ′ − y 2 = e−t
y (0) = −1
Multipliquemos os dois lados da equação por µ (t) :
µy ′ − µ y 2 = µe−t
Suponhamos que
−µ y 2 = µ′ y
e temos
(µy) ′ = µe −t
∫
µy = µe −t dt
y =
∫
µe −t dt
µ
Concluímos que se for possível encontrar uma tal função µ então poderemos
encontrar as soluções da equação. Mas encontrar uma tal função µ, que
chamaremos de FATOR INTEGRANTE, é relativamente simples:
yµ ′ = −µ y 2 (y ≠ 0) ⇒ µ′ = − µ 2 ⇒
⇒ µ′
µ = −1 2 ⇒ d dt ln |µ| = −1 2 ⇒
⇒
ln |µ| = − t 2 + c ⇒ |µ| = ke− t 2 , k > 0 ⇒
⇒ µ = ke − t 2 , k ∈ R.
Assim, voltando para o PVI, temos
y =
∫
ke
− t 2 e −t dt
ke − t 2
5
= − 2 3t
3e− 2 + c
e − t 2

e como
segue que
y (0) = −1
− 2 3 + c = −1
e portanto
e
c = − 1 3
y = − 2 3 e−t − 1 3 e t 2
Teorema: Sejam p, g funções reais contínuas definidas em um intervalo
aberto I e t 0 ∈ I. O PVI
{ y ′ + p (t) y = g (t)
admite uma única solução
y (t 0 ) = y 0
φ : I → R.
Prova:
Vamos proceder da mesma maneira que procedemos no exemplo acima.
Inicialmente encontremos uma função µ que satisfaça
É trivial vermos que
µ ′ = pµ.
R t
p(s)ds
t
µ (t) = e 0
satisfaz o desejado. µ é chamada de FATOR INTEGRANTE. Temos:
Como
segue que
y ′ + py = g ⇒ y ′ µ + pµy = µg ⇒
⇒
y ′ µ + µ ′ y = µg ⇒ (yµ) ′ = µg ⇒
∫ t
⇒ yµ (t) = g (s) µ (s) ds + k ⇒
t 0
⇒ y = e − R (∫
t
t R
)
p(s)ds
s
t 0 t p(u)du 0 g (s) ds + k
y (t 0 ) = y 0
k = y 0
t 0
e
e que a solução do PVI é
y = e − R (∫
t
t R
)
p(s)ds
s
t 0 t
e
p(u)du 0 g (s) ds + y 0 .
t 0
6

Exemplos:
1) {
y ′ + 2ty = t
y (0) = 0
Aplicando a fórmula acima temos
y = e − R (∫ t
t
0 2sds e R )
s
0 2udu sds = 1 2 − 1 .
2 e−t2
0
2) { ty ′ + 2y = 4t 2
y (1) = 2
Inicialmente dividimos os dois lados da equação por t. O intervalo aberto
onde as funções p e g estão definidas e são contínuas é (0, +∞) (o maior aberto
contendo o ponto da condição inicial t 0 = 1).
Temos
y = e − R t 2
1
s ds (∫ t
1
e R s
1
3) {
y ′ − 2ty = 1
y (0) = 1
)
2
u du 4sds + 2 = t 2 + 1 t 2
Aplicando a fórmula deduzida acima obtemos
y = e − R (∫ t
t
0 (−2s)ds e R )
s
0 (−2u)du ds + 1 =
(∫ t
)
= e t2 e −s2 ds + 1 .
0
0
Observe que a função que aparece no integrando não possui primitiva elementar.
Definindo a função
temos que
Erf (t) = √ 2 ∫ t
e −s2 ds
π
y (t) = e t2 (√ π
2 Erf (t) + 1 )
Com a ajuda de métodos numéricos podemos esboçar seu gráfico:
Também podemos obter algumas informações sobre o comportamento da
solução. Por exemplo, calculemos o limite de y (t) quando t tende a infinito.
Para isso, inicialmente calculemos
lim Erf (t) = lim
t→+∞
t→+∞
∫
2 t
√ π
0
0
e −s2 ds = 2 √ π
7
lim
t→+∞
∫ t
0
e −s2 ds = ∗

Chamando
temos que
Resta calcularmos L :
L =
∫ ∞
−∞
e −s2 ds
2
lim Erf (t) = √ . L
t→+∞ π 2 = √ L . π
L 2 =
=
∫ +∞ ∫ +∞
−∞ −∞
∫ +∞ ∫ 2π
0
= π.
0
e −x2 −y 2 dxdy =
e −r2 rdrdθ =
e
Logo
Assim
L = √ π
lim Erf (t) = 1
t→+∞
(√ )
π
lim y (t) = lim
t→+∞ t→+∞ et2 2 Erf (t) + 1 = +∞.
EXERCÍCIOS:
1) Desenhe um campo de direções para a equação dada e com base em
uma inspeção do campo descreva como as soluções se comportam para grandes
valores de t.
a)y ′ + 3y = t + e −2t
b)y ′ + y = te −t + 1
c)y ′ − 2y = 3e t
d)y ′ + 2ty = 2te −t2
e)2y ′ + y = 3t
f)y ′ + y = 5 sin 2t
2) Determine as soluções gerais das equações acima e use-as para determinar
como as soluções se comportam para grandes valores de t.
3) Ache a solução do PVI proposto:
{ y
a)
′ − y = 2te 2t
{
y (0) = 1
y
b)
′ + 2 t y = cos t
t 2
{ y (π) = 0
ty
c)
′ + 4t 2 y = t
y (−1) = 0
4) Considere o PVI {
y ′ − 1 2 y = 2 cos t
y (0) = a
8

a) Desenhe um campo de direções. Qual o comportamento das soluções para
grandes valores de t O comportamento depende da escolha do valor inicial a
Se depender estime o valor de a 0 , valor de a para o qual ocorre a transição
de um tipo de comportamento para o outro.
b) Resolva o PVI e determine a 0 .
c) Descreva o comportamento da solução correspondente a a 0 .
5) Considere o PVI
{ ty ′ + (t + 1) y = 2te −t
y (1) = a
a) Desenhe um campo de direções. Qual o comportamento das soluções para
t → 0 O comportamento depende da escolha do valor inicial a Se depender
estime o valor de a 0 , valor de a para o qual ocorre a transição de um tipo de
comportamento para o outro.
b) Resolva o PVI e determine a 0 .
c) Descreva o comportamento da solução correspondente a a 0 .
6) Considere o PVI {
y ′ + 2 3 y = 1 − t 2
y (0) = y 0
Determine o valor de y 0 para o qual a solução toca, mas não cruza, o eixo t.
7) Ache a solução geral
a)y ′ + ( )
1
t y = sin t, t > 0 d)ty ′ + 2y = e t , t > 0
b)y ′ + 2y = 2e −t + t e)3y ′ − 2y = cos t
c)2y ′ + y = t − 1
8) Considere os PVI’s
{ ty
i)
′ + 2y = t 2 − t + 1
{ y (1) = 1 2
ty
ii)
′ + y = e t
{
y (1) = 1
ty
iii)
′ + 2y = sin t
y (π) = 1 π
Para cada um dos problemas acima:
a) Determine a solução do PVI.
b) Faça um gráfico da solução.
c) Determine o intervalo em que a solução é válida.
d) Determine o comportamento da solução quando t se aproxima das extremidades
do intervalo.
9

9) Considere o PVI {
y ′ − 3 2y = 3t + 2et
y (0) = y 0
Determine o valor de y 0 que separa as soluções que crescem positivamente
quando t → +∞ das que crescem negativamente. Como se comporta solução
que corresponde a esse valor crítico de y 0
10) Mostre que se a e λ são constantes positivas e b é um número real
qualquer , toda solução da equação
y ′ + ay = be −λt
tem a propriedade de que y → 0 quando t → +∞.
2.2 Equações Redutíveis a Forma Linear
I- A Equação de Bernoulli
y ′ + p (t) y = q (t) y n , n ∈ Z.
Se n = 0 ou n = 1 então a equação é linear e já sabemos como resolvê-la.
Para n ≠ 0 e para n ≠ 1 consideramos a seguinte mudança de coordenadas
v = y 1−n
e temos
dv
−n dy
= (1 − n) y
dt
dt
dv
dy
dt
=
dt 1 − n yn
dv
dt
1 − n yn + p (t) y = q (t) y n (÷y n )
dv
dt
1 − n + p (t) y1−n = q (t)
v ′ + (1 − n) p (t) v = (1 − n) q (t)
sendo a última equação linear.
Exemplo:
Fazemos
{
y ′ + 1 t
y = (cos t) y−2
y (1) = 1
v = y 3
, t > 0
10

e obtemos o problema
{
v ′ + 3 t v = 3 cos t
v (1) = 1
.
II- A Equação de Riccati
y ′ + p (t) y + q (t) y 2 = f (t)
Teorema: Se y 1 e y 2 são soluções da equação de Riccati então
é solução da equação de Bernoulli
z = y 2 − y 1
z ′ + (p (t) + 2y 2 q (t)) z = q (t) z 2 .
Prova: Basta efetuar o cálculo para comprovar.
Exemplo:Sabendo que
é solução de
encontre outra solução.
Pelo método acima temos que
y 2 = t
y ′ + t 3 y − t 2 y 2 = 1
z = t − y 1
é solução de
Fazendo
z ′ − t 3 z = −t 2 z 2 .
v = 1 z
obtemos
cuja solução é
v = e − t4 4
v ′ + t 3 v = t 2
(∫
)
e t4 4 t 2 dt + c .
Logo
y 1 = t −
e t4 4
∫
e
t 4 4 t 2 dt + c
é outra solução.
11

2.3 Equações Separáveis
Uma EDO de primeira ordem
y ′ = f (x, y)
é dita SEPARÁVEL se for possível escrevermos
f (x, y) = M (x)
N (y) .
Exemplos:
1)
é separável.
y ′ = x e y
2)
não é separável.
y ′ = sin (xy)
Soluções de Equações Separáveis:
Dada a equação
temos que
e assim
∫
y ′ = M (x)
N (y)
N (y) y ′ = M (x)
∫
N (y) y ′ dx = M (x) dx
Fazendo a mudança de variável, na primeira primitiva, dada por
y = y (x)
temos que
e assim
∫
dy = y ′ dx
∫
N (y) dy = M (x) dx
e as soluções da EDO são dadas implicitamente por
g (y) − h (x) = c.
12

Observação: É comum escrevermos uma EDO separável da seguinte forma
M (x) dx + N (y) dy = 0
Exemplos:
1)
y ′ =
x2
1 − y 2
∫ (1
− y
2 ) ∫
dy =
x 2 dx
2) {
Temos
y − 1 3 y3 = x3
3 + c
y ′ = 3x2 +4x+2
2(y−1)
y (0) = −1
∫
(2y − 2) dy = ( 3x 2 + 4x + 2 ) dx
∫ (3x
(2y − 2) dy =
2 + 4x + 2 ) dx
y 2 − 2y = x 3 + 2x 2 + 2x + c
Como
y (0) = −1
temos
c = 3
e assim a solução é dada implicitamente por
y 2 − 2y = x 3 + 2x 2 + 2x + 3
3)
y ′ = y cos x
1 + 2y 2
1 + 2y 2
dy = cos xdx
y
ln |y| + y 2 − sin x = c
13

2.4 Equações Exatas
——–
Antes de estudarmos as equações separáveis vamos inicialmente rever alguns
pré-requisitos de Cálculo Vetorial e Álgebra Linear.
Definição: Um campo de vetores em U ⊂ R 2 , aberto, é uma função
F : U → R 2
Exemplos:1)
2) Dado uma função
temos que
∇V (x, y) =
é o gradiente de V em (x, y) .
F (x, y) = (x, −y)
V : U → R
( )
∂V ∂V
(x, y) ,
∂x ∂y (x, y)
é um campo de vetores.
∇V : U → R 2
Definição: Sejam
um campo de vetores diferenciável e
F : U → R 2
α : [a, b] → U
uma curva diferenciável. Definimos a integral de F ao longo de α por
∫ ∫ b
F dr = F (α (t)) α ′ (t) dt
Notação:
Denotando
α
a
F (x, y) = (P (x, y) , Q (x, y))
α ′ (t) = (x ′ (t) , y ′ (t))
temos
∫
α
F dr =
=
∫ b
a
∫ b
a
(P (x (t) , y (t)) , Q (x (t) , y (t))) (x ′ (t) , y ′ (t)) dt =
[P (x (t) , y (t)) x ′ (t) + Q (x (t) , y (t)) y ′ (t)] dt = ∗
14

temos
Escrevendo
x ′ (t) = dx
dt , y′ (t) = dy
dt
∫
∗ = P dx + Qdy
α
Definição: F : U → R 2 é dito GRADIENTE se existir V : U → R tal que
F = ∇V. A função V é chamada de POTENCIAL.
Exemplo:
é gradiente. De fato, basta considerar
F (x, y) = ( x 2 , 3y )
V (x, y) = x3
3 + 3y2
2 .
Definição: F : U → R 2 , F (x, y) = (P (x, y) , Q (x, y)) é dito FECHADO
se P y = Q x .
Teorema:
a)
b)
F gradiente e C 1 ⇒ F é fechado.
∫
F gradiente e C 0 ⇒
α
F dr = V (α (b)) − V (α (a))
onde α : [a, b] → R 2 é diferenciável e V é um potencial de F.
c)
∫
F gradiente e C 0 ⇒ F dr = 0 onde α é uma curva diferenciável fechada.
α
d)
∫
F dr = 0 qualquer que seja α curva diferenciável fechada, F ∈ C 0 ⇒
α
e)
⇒
F é gradiente.
F diferenciável, fechado e U simplesmente conexo ⇒ F é gradiente.
15

Teorema de Green: Sejam
F : U → R 2
de classe C 1 e α uma curva fechada, simples e suave por partes. Então
∫
∫ ∫
P dx + Qdy = (Q x − P y ) dA
onde D é a região limitada pelo traço de α.
Como
α
Prova do Teorema das Equivalências:
a) Se F é gradiente então existe V tal que
D
F = (V x , V y )
V yx = V xy
temos que F é fechado.
b) Sendo F gradiente temos
∫
∫
F dr = V x dx + V y dy =
α
=
=
α
∫ b
a
∫ b
c) Imediato a partir de b).
d) Definimos
a
(V x x ′ + V y y ′ )dt =
d
(V ◦ α)dt = V (α (b)) − V (α (a)) .
dt
∫
V (x, y) =
α
F dr
onde α é um caminho qualquer ligando um ponto (x 0 , y 0 ) fixado a (x, y) .
V está bem definida pois a hipótese garante que a integral não depende do
caminho.
Tomando o caminho α como a justaposição dos caminhos α 1 e α 2 onde
α 1 é o caminho retilíneo ligando (x 0 , y 0 ) a (x, y 0 )
α 2 é o caminho retilíneo ligando (x, y 0 ) a (x, y)
temos
V (x, y) =
=
∫
P dx + Qdy =
α
∫ x ∫ y
P dx + Qdy
x 0 y 0
16

e assim
V x = P, V y = Q.
e) Basta aplicarmos o Teorema de Green
∫ ∫ ∫
F dr = (Q x − P y ) dA = 0.
α
D
Exemplo: Observe a importância do aberto ser simpesmente conexo. Considere
U = {(x, y) ∈ R 2 |ρ 2 1 ≤ x 2 + y 2 ≤ ρ 2 2}
e
É fácil verificar que
F (x, y) =
( )
y
x 2 + y 2 , −x
x 2 + y 2
P y = Q x
e que portanto F é fechado. No entanto, considerando o caminho fechado
α (t) = (r cos t, r sin t) , t ∈ [0, 2π] , ρ 1 < r < ρ 2
temos que
∫
α
F dr = 2π ≠ 0.
Definição:
T : R 2 → R
é uma TRANSFORMAÇÃO LINEAR desde que
T (αu + βv) = αT (u) + βT (v) , ∀u, v ∈ R 2 , ∀α, β ∈ R.
Definição:
(
R
2 ) ∗
= {T : R 2 → R|T é linear}
é chamado de ESPAÇO DUAL de R 2 .
Teorema:
( ) R
2 ∗
é um espaço vetorial de dimensão 2 e uma base desse
espaço é {dx, dy} onde
dx (x, y) = x
dy (x, y) = y
Prova:
17

Vamos provar apenas que
é um conjunto LI.
Se
então
Assim
{dx, dy}
αdx + βdy = 0
(αdx + βdy) (x, y) = 0, ∀ (x, y) ∈ R 2 .
(αdx + βdy) (1, 0) = α = 0
(αdx + βdy) (0, 1) = β = 0
Definição:
Uma 1-FORMA DIFERENCIAL é uma aplicação
ω : U ⊂ R 2 → ( R 2) ∗
Escrevemos
ω (x, y) = P (x, y) dx + Q (x, y) dy
Um exemplo bem conhecido é a diferencial de
f : U ⊂ R 2 → R
df (x, y) = ∂f
∂f
(x, y) dx + (x, y) dy
∂x ∂y
Definição:
a)Uma 1-forma ω é chamada de EXATA se existe f tal que
ω = df.
b) ω = P dx + Qdy é dita FECHADA se
P y = Q x
c) A integral de uma 1-forma ω = P dx + Qdy ao longo de um caminho
diferenciável
α(t) = (x (t) , y (t)) , a ≤ t ≤ b
é definida por
∫
α
P dx + Qdy =
∫ b
a
[P (x (t) , y (t)) x ′ (t) + Q (x (t) , y (t)) y ′ (t)] dt
18

Observação:
É claro que
ω = P dx + Qdy
é exata se e somente se o campo de vetores
F = (P, Q)
for gradiente.
O próximo teorem tem demonstração análoga ao teorema das equivalências:
Teorema: Dados U ⊂ R 2 um aberto simplesmente conexo e ω = P dx+Qdy
uma 1-forma diferencial de classe C 1 temos que são equivalentes:
a) ω é exata;
b) ω é fechada;
c) ∫
para qualquer caminho fechado em U.
P dx + Qdy = 0
α
Uma equação diferencial
Equações Exatas
N (x, y) y ′ + M (x, y) = 0 (*)
onde M, N ∈ C 1 em U ⊂ R 2 aberto simplesmente conexo é dita EXATA se
Seja
uma função tal que
então
M y = N x .
f : U → R
∂f ∂f
= M,
∂x ∂y = N
N (x, y) y ′ + M (x, y) = 0 ⇒ ∂f
∂y (x, y) y′ + ∂f (x, y) = 0 ⇒
∂x
⇒
d (f (x, y (x))) = 0 ⇒ f (x, y (x)) = cte
dx
Concluímos que as soluções de (∗) possuem gráficos contidos nas curvas de
nível da f.
19

Na notação diferencial temos
Exemplo:
Ny ′ + M = 0 ⇒ N dy
dx + M = 0 ⇒
⇒ Mdx + Ndy = 0 ⇒ df = 0.
Como
(2xy + 1) dx + ( x 2 + 4y ) dy = 0
segue que a equação é exata.
Resolvemos
e obtemos
M y = ∂ (2xy + 1) = 2x
∂y
N x = ∂ (
x 2 + 4y ) = 2x
∂x
{
∂f
∂x = 2xy + 1
∂f
∂y = x2 + 4y
f (x, y) = x 2 y + 2y 2 + x
Logo as soluções são dadas implicitamente por
Observação:
a) Uma função f satisfazendo que
x 2 y + 2y 2 + x = c
F = (P, Q) =
( ∂f
∂x , ∂f )
∂y
é chamada de FUNÇÃO POTENCIAL do campo F.
b) Se
P = ∂f
∂x , Q = ∂f
∂y
então f é dita uma INTEGRAL PRIMEIRA da equação
P dx + Qdy = 0.
Exemplo:
não é exata. Multiplicando por
−ydx + xdy = 0
1
x 2
20

obtemos
− y x 2 dx + 1 x dy = 0
que é exata.
Chamamos
ϕ (x, y) = 1 x 2
de fator integrante.
Resolvendo
obtemos
{
∂f
∂x = − y x 2
∂f
∂y = 1 x
f (x, y) = y x
e as soluções são dadas implicitamente por
Definição: Se
não for exata mas
y
x = c
Mdx + Ndy = 0
µ (Mdx + Ndy) = 0
for exata então µ é chamado de FATOR INTEGRANTE.
DICAS DE COMO ENCONTRAR FATORES INTEGRANTES:
1) É possível encontrar µ = µ (x) se
não depender de y. De fato se
M y − N x
N
µ (Mdx + Ndy) = 0
for exata então
e assim
µM y + µ y M = µN x + µ x N
µ x
µ = M y − N x
⇒ (ln µ) ′ = M y − N x
⇒ µ (x) = e R My −Nx
N
N
N
2) Analogamente é possível encontrar µ = µ (y) se
N x − M y
M
21

não depender de x
µ (y) = e R Nx−My
M
Exemplos:
1)
não é exata.
Como
temos que
ydx + ( x 2 y − x ) dy = 0
M y − N x
N
= − 2 x
µ (x) = e R − 2 x dx = 1 x 2
é um fator integrante.
Assim
1 ( (
ydx + x 2
x 2 y − x ) dy ) = 0
é exata. Resolvendo o sistema
{
∂f
∂x = − y x 2
∂f
∂y = y − 1 x
obtemos
2)
não é exata. Como
depende só de y temos que
é um fator integrante. Assim
f (x, y) = − y x + y2
2
−2xydx + ( 3x 2 − y 2) dy = 0
N x − M y
M
= − 4 y
R
µ (y) = e − 4
y dy = 1 y 4
− 2x
y 3 dx + ( 3x
2
y 4 − 1 y 2 )
dy = 0
é exata e as soluções são dadas implicitamente por
− x2
y 3 + 1 y = c.
22

Método Prático
Algumas diferenciais podem auxiliar na solução de certas equações:
1)d (x α ) = αx α−1 dx
2)d (xy) = ydx + xdy
( ) x ydx − xdy
3)d =
y y 2
4)d ( x 2 + y 2) = 2xdx + 2ydy
(
5)d ln x )
ydx − xdy
=
y
xy
(
6)d arctan x )
ydx − xdy
=
y x 2 + y 2
Exemplos:
1)
ydx + ( x 2 y − x ) dy = 0 ⇒
⇒
⇒
⇒
⇒
⇒
ydx + x 2 ydy − xdy = 0 ⇒
ydx − xdy
x 2 + ydy = 0 ⇒
(
d − y ) ( ) y
2
+ d = 0 ⇒
x 2
d
(− y )
x + y2
= 0 ⇒
2
− y x + y2
2 = c
23

2)
ydx + ( 1 + y 2 − x ) dy = 0 ⇒
⇒
⇒
⇒
⇒
ydx + dy + y 2 dy − xdy = 0 ⇒
( )
ydx − xdy 1
y 2 +
y 2 + 1 dy = 0 ⇒
( ) x
d + d
(− 1 )
y y + y = 0 ⇒
( x
d
y − 1 )
y + y = 0 ⇒
⇒ x y − 1 y + y = c.
2.5 Equações Homogêneas
Uma EDO
é dita HOMOGÊNEA se
f
y ′ = f (x, y)
( ) x
(x, y) = F
y
para alguma função real de uma variável real F .
Exemplos:
1)
é homogênea. De fato,
2)
é homogênea. De fato
y ′ = y2 + 2xy
x 2
y 2 + 2xy
( y
) 2 x
x 2 = + 2
x y
y ′ = ln x − ln y
ln x − ln y = ln x y
Como Resolver Equações Homogêneas
24

Dada a equação
( ) x
y ′ = f (x, y) = F
y
fazemos
v = y x
e temos
e assim nossa equação fica
que é separável.
y = vx
dy
dx = v + dv
dx x
v + dv
dx x = F (v)
dv
dx = F (v) − v
x
Exemplo:
Assim ficamos com
y ′ = y2 + 2xy
( y
) 2 y
x 2 = + 2
x x
F (v) = v 2 + 2v
Temos
e assim
e portanto
dv
dx = v2 + 2v − v
= v2 + v
x x
dv
v (v + 1) = dx x
v =
y =
cx
1 − cx
cx2
1 − cx
25

2.6 O Teorema de Existência e Unicidade
Teorema: Seja o PVI { y ′ = f (t, y)
y (t 0 ) = y 0
.
Suponhamos que as funções f e ∂f
∂y
e que o ponto (t 0 , y 0 ) satisfaz
R :
são contínuas em
α ≤ t ≤ β
γ ≤ y ≤ δ
α < t 0 < β, γ < y 0 < δ.
Então existe h > 0 tal que em (t 0 − h, t 0 + h) ⊂ (α, β) existe uma única função
φ solução do PVI.
Antes de darmos uma idéia da prova do teorema vejamos alguns exemplos:
e
1) Considere o PVI { y ′ = 3√ y
y (0) = 0 .
Observe que as funções
y 2 =
y 1 ≡ 0
{ √ ( 2
3 t) 3
, t ≥ 0
0, t < 0
são duas soluções distintas do PVI. isto não contradiz o teorema pois
∂ ( √ 3
y )
= 1
∂y 3 3√ y 2
não é contínua em nenhum intervalo contendo (0, 0) .
2) {
y ′ = y 2
y (0) = 1
A equação é separável e facilmente obtemos
y = 1
1 − t .
Note que encontramos uma solução, mas o fato dela não estar definida em
t = 1 é de certa forma inesperado. De fato, a equação não dá nenhuma pista
26

sobre eventuais problemas em t = 1. De qualquer forma o teorema verifica-se, já
que ele garante apenas que existe uma única função definida em uma vizinhança
de t 0 = 0 que é solução do PVI.
O Método de Picard e uma idéia da prova do Teorema
Para simplificar a apresentação, consideremos o caso particular
{ y ′ = f (t, y)
e f e ∂f
∂y contínuas em R :
y (0) = 0
−a ≤ t ≤ a
−b ≤ y ≤ b
A prova baseia-se no MÉTODO DAS APROXIMAÇÕES SUCESSIVAS (
Método de Picard).
Inicialmente observemos que se φ é uma solução do PVI então temos
∫ t
0
φ ′ (s) = f (s, φ (s))
φ ′ (s) ds =
φ (t) − φ (0) =
φ (t) =
∫ t
0
∫ t
0
∫ t
0
f (s, φ (s)) ds
f (s, φ (s)) ds
f (s, φ (s)) ds
Consideremos uma sequência de funções dada por
φ 0 (t) = 0
φ 1 (t) =
φ 2 (t) =
φ n (t) =
∫ t
0
∫ t
0
∫ t
.......
0
f (s, φ 0 (s)) ds
f (s, φ 1 (s)) ds
f (s, φ n−1 (s)) ds
Se a seqũencia for convergente então a função limite será uma solução. Para
resolvermos tal problema devemos antes de mais nada verificarmos se φ n está
bem definida.
27

[−a, a] ⊂ Dom (φ n )
ou equivalentemente
I (φ n ) ⊂ [−b, b]
|φ n (t)| ≤ b
Como a função f é contínua em R temos que existe M > 0 tal que
e assim, se
então
Tomando
temos que
|φ n (t)| =
em (−h, h) .
É trivial verificarmos que
≤
≤
φ 0 +
|f (t, y)| ≤ M
∣
|t| ≤ b M
∫ t
0
∫ t
0
∫ t
0
h = min{a,
f (s, φ n−1 (s)) ds
∣ ≤
|f (s, φ n−1 (s))| ds ≤
Mds ≤ M |t| ≤ b.
|φ n (t)| ≤ b
b
M }
n∑
(φ i − φ i−1 ) = φ n
i=1
Assim, para provarmos a convergência da sequência φ n basta verificarmos a
convergência da série
n∑
(φ i − φ i−1 ) .
i=1
É suficiente verificarmos a convergência de
n∑
|φ i − φ i−1 |
i=1
28

Como ∂f
∂y é contínua temos que f é LIPSCHITZIANA com relação a variável
y isto é
∃k > 0, |f (t, y 1 ) − f (t, y 2 )| ≤ k |y 1 − y 2 |
Assim
|φ 2 (t) − φ 1 (t)| =
Por indução temos
≤
≤
≤
∣
∫ t
0
∫ t
0
∫ t
0
∫ t
0
[f (s, φ 1 (s)) − f (s, φ 2 (s))] ds
∣ ≤
|f (s, φ 1 (s)) − f (s, φ 2 (s))| ds ≤
k |φ 1 (s) − φ 0 (s)| ds ≤
kM |s| ≤ kM t2 2
|φ n − φ n−1 | ≤ k n−1 M hn
n! .
Assim temos que verificar que a série
é convergente.
Como
∞∑
i=1
k n−1 M hn
n! = M k
(hk) n+1
(n+1)!
(hk) n
n!
∞∑ (hk) n
i=1
= hk
n + 1 → 0
o teste da razão garante a convergência da série.
Logo existe φ tal que
φ n → φ.
≤ kM
h2
2 .
Provemos agora a unicidade.
Suponhamos que φ e ψ sejam soluções do PVI. Assim
Desta forma
φ (t) =
ψ (t) =
|φ (t) − ψ (t)| ≤ k
≤
k
∫ t
0
∫ t
0
∫ t
0
∫ t
0
n!
f (s, φ (s)) ds
f (s, ψ (s)) ds
|f (s, φ (s)) − f (s, ψ (s))| ds ≤
|φ (s) − ψ (s)| ds.
29

temos
Chamando
u (t) =
∫ t
0
|φ (s) − ψ (s)| ds
u (0) = 0
u ′ (t) = |φ (t) − ψ (t)|
u ′ − ku ≤ 0
e −kt (u ′ − ku) ≤ 0
(
e −kt u ) ′
≤ 0
Observe que concluímos que uma função positiva ou nula, passando pela origem
tem derivada negativa. A única possibilidade é que
u ≡ 0
e portanto
logo
∫ t
0
|φ (s) − ψ (s)| ds = 0, ∀t
φ = ψ.
Exemplo:
Vamos utilizar o método das aproximações sucessivas para encontrarmos a
solução do PVI { y ′ = 2t (1 + y)
Temos
y (0) = 0
φ 0 (t) = 0
φ 1 (t) =
φ 2 (t) =
φ n (t) =
φ n (t)
Exercícios:
→
∫ t
0
∫ t
0
...
∫ t
0
∞∑
n=0
2s (1 + φ 0 (s)) ds = t 2
2s (1 + φ 1 (s)) ds = t 2 + t4 2
2s (1 + φ n−1 (s)) ds = t 2 + t4 2
t 2n
n!
= e t2 − 1.
+ ... +
t2n
n!
30

1) Resolva a EDO:
a)y ′ = x2
y
b)y ′ + y 2 sin x = 0
c)y ′ = ( cos 2 x ) ( cos 2 2y )
d) dy
dx = x−e−x
y+e y
2) Resolva o PVI {
y ′ = 1+3x2
3y 2 −6y
y (0) = 1
e determine o intervalo no qual a solução é válida.
3) Resolva o PVI
{ y ′ = 2−ex
3+2y
y (0) = 0
e determine em que ponto a solução atinge seu valor máximo.
4) Resolva o PVI e determine a dependência , em relaão ao valor inicial y 0 ,
do intervalo sobre o qual a solução existe:
{ y ′ = −4t {
a)
y
y
b)
′ + y 3 = 0
y (0) = y 0 y (0) = y 0
5) Determinar se as equações são ou não exatas. Para as exatas, achar a
solução
a) (2x + 3) + (2y − 2) y ′ = 0 d) dy
dx = − ax−by
bx−cy
b) ( 3x 2 − 2xy + 2 ) dx + ( 6y 2 − x 2 + 3 ) dy = 0 e) ( y
x + 6x) dx + (ln x − 2) dy = 0
c) dy
dx = − ax+by
x
y
bx+cy
f) dx + dy = 0
(x 2 +y 2 ) 3 2 (x 2 +y 2 ) 3 2
6) Prove que qualquer equação separável também é exata.
7) Resolva as equações homogêneas:
a) dy
dx =
2xy
3y 2 −x 2
b) dy
dx = 3y2 −x 2
2xy
3 Aplicações de EDO’s de Primeira Ordem
31

3.1 Famílias de Curvas Planas
Sejam U ⊂ R 2 aberto , Λ ⊂ R e
F : U × Λ → R.
Uma família a um parâmetro de curvas planas é uma família de curvas
obtidas implicitamente por
F (x, y, λ) = 0.
Exemplos:
1)
2)
x 2 + y 2 = λ 2 , λ ≥ 0
y = λx
PROBLEMA: Dado uma família a um parâmetro de curvas planas, encontrar
uma EDO tal que os gráficos das soluções estejam contidos nos traços
das curvas da família.
Exemplos:
1)
Derivando com relação a x obtemos
y − x − λ = 0
y ′ = 1.
2)
Temos
y − 2λx 2 − λ = 0
λ =
y
2x 2 + 1
y ′ − 4λx = 0
y ′ = 4λx
y ′ =
4xy
2x 2 + 1
Observação:
Observe que, de acordo com o Teorema da Função Implícita, a equação
define λ como função de (x, y) quando
f (x, y, λ) = 0
∂f
∂λ ≠ 0.
32

Definição:
a) Duas funções diferenciáveis
são ortogonais em x 0 ∈ I se
φ, ψ : I ⊂ R → R
φ ′ (x 0 ) ψ ′ (x 0 ) = −1
b) Duas famílias a um parâmetro de curvas planas diferenciáveis
F (x, y, λ) = 0
G (x, y, µ) = 0
são ditas ortogonais quando as λ− curvas forem ortogonais as µ−curvas em
todos os pontos onde se encontrarem.
PROBLEMA: Encontrar uma família de curvas ortogonais a uma família
dada.
Para resolvermos este problema procedemos da seguinte maneira: Seja
F (x, y, λ) = 0
a família dada.
Encontramos uma EDO que tenha suas soluções nos gráficos das curvas da
família
f (x, y, y ′ ) = 0
Em seguida resolvemos a EDO
f
(x, y, − 1 )
y ′ = 0
A solução da EDO acima fornecerá a família ortogonal.
Exemplos:
1)
Temos
x 2 + y 2 + λ 2 = 0
2x + 2yy ′ = 0
x + yy ′ = 0
y ′ = − x y
Consideramos a nova EDO
− 1 y ′ = −x y
33

e temos, usando separação de variáveis, que as soluções são
2)
A EDO da família ortogonal é
cuja solução é
3.2 O Instante da Morte
y = kx
y − 2λx 2 − λ = 0
y ′ =
4xy
2x 2 + 1
− 1 y ′ =
4xy
2x 2 + 1
2y 2 + x 2 + ln |x| = k
Somos peritos policiais e encontramos em um local o corpo de um homem
morto com temperatura igual a 30 graus.
Precisamos determinar o horário em que ocorreu a morte.
Para isso precisamos de um pouco de Física.
Lei de Resfriamento de Newton: A temperatura superficial de um corpo
altera-se proporcionalmente a diferença de temperatura entre o corpo e a vizinhança
do corpo.
Voltemos para a nossa investigação policial. Suponhamos que a temperatura
no local do crime seja
T = 20 o
Chamaremos
a temperatura do corpo no instante t.
A Lei de Resfriamento nos diz que
y (t)
y ′ (t) = −k (y (t) − 20)
Assim
Temos
{ y ′ = −ky + 20k
y (0) = 30 o
∫
y ′ = −ky + 20k ⇒
∫
dy
y − 20 =
−kdt ⇒
⇒ y = 20 + ce −kt 34

Como
segue que
e assim
y (0) = 30 = 20 + c
c = 10
y = 20 + 10e −kt
Para que possamos determinar a constante de proporcionalidade k, efetuamos
após 2 horas outra medição da temperatura do cadáver e encontramos
Assim
Logo
y (2) = 23 o
23 = 20 + 10e −k2
k = − ln 3
10
2
= . 601 99
−. 601 99t
y = 20 + 10e
e assim, admitindo que a temperatura de uma pessoa viva é de 37 o temos
Usando uma regra de três temos
37 = 20 + 10e −. 601 99t ⇒ t = −. 881 46
1 hora = 60 minutos
. 881 46 horas = x minutos
x = 60 (. 881 46) = 52. 888
que é aproximadamente 53 minutos.
Concluímos que a morte ocorreu 53 minutos antes de chegarmos ao local do
crime.
3.3 Dinâmica de Populações
A Dinâmica de Populações estuda a evolução do número de habitantes de
uma determinada espécie quando o tempo passa.
O caso mais elementar é aquele em que fazemos a hipótese
A Taxa de crescimento é proporcional ao número de habitantes
35

Modelemos tal situação
t : tempo
p (t) : população no tempo t
p (0) = p 0 : populção inicial
Assim { p ′ = kp
p (0) = p 0
É trivial obtermos
p (t) = p 0 e kt
Neste caso só temos duas possibilidades: ou k > 0 e daí o crescimento da
população é exponencial, o que irá ocasionar uma superpopulação; ou k < 0, o
que provocará a extinção da população.
Concluímos que este modelo não é razoável.
O modelo conhecido como modelo logístico substitui a constante k por uma
função que depende da população
p ′ = h (p) p
e satisfazendo que quando a população aumenta a taxa h(p) diminui. Um modelo
razoável é
{ p ′ = (r − ap) p
onde
É comum escrevermos
e assim nosso modelo é
p (0) = p 0
a, r > 0.
k = r a
{
p ′ = r ( 1 − p )
k p
p (0) = p 0
Observe o campo de direções
A equação é separável e pode ser facilmente resolvida. Vamos proceder uma
análise qualitativa antes de resolvê-la.
Como
(
p ′ = r 1 − p )
p
k
temos
e também
0 < p < k ⇒ p ′ > 0 ⇒ p crescente
p > k ⇒ p ′ < 0 ⇒ p decrescente
p ′ =
(
r 1 − p )
p = f (p)
k
p ′′ = f ′ (p) p ′ = f ′ (p) f (p)
36

Assim
0 < p < k { f
2 ⇒ ′ (p) > 0
⇒ p ′′ > 0 ⇒ concavidade para cima
f (p) > 0
{
k
f
< p < k ⇒
′ (p) < 0
⇒ p ′′ < 0 ⇒ concavidade para baixo
2
f (p) > 0
{ f
p > k ⇒
′ (p) < 0
⇒ p ′′ > 0 ⇒ concavidade para cima
f (p) < 0
Podemos esboçar as soluções
A conclusão que chegamos é que existem duas popuções de equilíbrio (p = k, p = 0)
e que quando a população inicial for diferente das populações de equilíbrio, ela
tenderá a população de equilíbrio, quando o tempo passar.
É fácil resolvermos explicitamente, usando separação de variáveis
( 1
p + 1
k
1 − p k
dp
( )
1 −
p
= rdt ⇒
p
k
)
dp = rdt ⇒
⇒
⇒
3.4 Curvas de Perseguição
p
ln
∣ 1 −
p ∣ = rt + c ⇒
k
p
∣ 1 −
p ∣ = cert
k
Imaginemos que um rato está alegre e contente comendo seu queijo quando
é avistado por um gato faminto. O gato foge, seguindo a direção vertical com
uma velocidade ν e o gato persegue o rato, sempre em sua direção com uma
velocidade ω.
Fixamos um sistema de coordenadas. O rato parte da origem (0, 0) e o gato
de um ponto (a, 0) .
Vamos estudar o movimento do gato.
Denotamos
y (x)
a curva descrita pelo gato em seu movimento.
Suponhamos que após um tempo t o gato esteja no ponto (x, y) .
Assim
tempo =
t =
espaço
velocidade
√
1 + (y ′ (u)) 2 du
∫ a
x
ϖ
37

Estudemos agora o movimento do rato
velocidade= espaço
tempo
Suponhamos que após o tempo t o rato esteja no ponto (0, q) .
Assim
ν = q t
t = q ν
Lembrando que o gato corre na direção do rato, temos que
Assim
−y ′ = q − y
x
q − y = −xy ′
q = y − xy ′
t = y − xy′
v
Logo, a equação diferencial que a curva descrita pelo gato satisfaz é
∫
√
a
y − xy ′ 1 + (y
x
′ (u)) 2 du
=
v
ϖ
Rescrevendo
ν
ϖ
∫ a
x
√
1 + (y ′ (u)) 2 du = y − xy ′
e derivando com relação a x dos dois lados
− ν √
1 + (y
ϖ
′ ) 2 = y ′ − xy ′′ − y ′
Finalmente obtemos
Chamamos
e obtemos
√
ν
1 + (y
ϖ
′ ) 2 = xy ′′
y ′ = p
ν √
1 + p
2
= xp ′
ϖ
1 ν
x ϖ = p ′
√
1 + p
2
38

Calculando a primitiva dos dois lados
∫
dp
√
1 + p
2
(√ )
− ln 1 + p2 − p
= ν ϖ ln x + c
= ν ϖ ln x + c
então
Observe que se
Assim
x = a
p = 0
0 = ν ϖ ln a + c
c = − ν ϖ ln a
Assim
(√ )
− ln 1 + p2 − p
ln
1
√
1 + p2 − p
= ν ϖ ln x − ν ϖ ln a
( x
) ν
ϖ
= ln
a
1
√
1 + p2 − p
=
( x
a
) ν
ϖ
1 =
(√ ) ( x
) ν
ϖ
1 + p2 − p
a
( x
) ν
√ (
ϖ x
) ν
1 + p
a 2 ϖ
= 1 + p
a
√
1 + p
2
=
1 + p 2 =
( a
x) ν
ϖ
+ p
( a
x)2ν
ϖ
( a
ν
ϖ
+ 2p + p
x) 2
1 =
p = 1 2
( a
x)2ν
ϖ
( a
ν
ϖ
+ 2p
x)
[ (x ) ν (
ϖ a
ν
ϖ
−
a x)
]
1 o Caso:
Chamando
ν
ϖ ≠ 1
c = ν ϖ
39

temos
Como
segue que
e portanto
p = 1 [ ] 1
2 a c xc − ac
x c
y = 1 [ 1 x c+1
]
2 a c c + 1 +
ac 1
c − 1 x c−1 + d
y = a [ 1
( x
)c+1
+ 1 ( a
) ] c−1
+ d
2 c + 1 a c − 1 x
y = a 2
d =
y (a) = 0
aϖν
ϖ 2 − ν 2
[ 1
( x
)c+1
+ 1 ( a
) ] c−1
+ aϖν
c + 1 a c − 1 x ϖ 2 − ν 2
Para sabermos o destino do rato precisamos calcular
{
lim y (x) = +∞, se c > 1
aϖν
x→0 + ϖ 2 −ν
, se 0 < c < 1
2
Logo se
c = ν ϖ > 1
ou seja se a velocidade do rato for maior que a do gato, o ratinho está salvo.
Porém, se
0 < c = ν ϖ < 1
ou seja, se a velocidade do gato for maior que a do rato então o tempo de vida
do ratinho está contado e é igual a
t = lim x→0 + y (x)
ν
=
aϖν
ϖ 2 −ν 2
ν
= aϖ
ϖ 2 − ν 2
2 o Caso:
Neste caso temos
e assim
Neste caso temos
e portanto o rato vence.
c = ν ϖ = 1
p = 1 [ x
2 a x]
− a
y = 1 [ ]
x
2
2 2a − a ln x + d
lim y (x) = +∞
x→0 +
40

4 Equações Diferenciais Ordinárias de Segunda
Ordem
Uma EDO de Segunda Ordem é uma equação do tipo
y ′′ = f(t, y, y ′ )
Será chamada de EDO de Segunda Ordem Linear se for do tipo
y ′′ + p (t) y ′ + q (t) y = g (t) .
Se g ≡ 0 então é chamada de EDO de Segunda Ordem Linear Homogênea.
Será chamada de EDO de Segunda Ordem Linear com Coeficeintes Constantes
se for do tipo
y ′′ + by ′ + cy = g (t) .
Se g ≡ 0 então é chamada de EDO de Segunda Ordem Linear com Coeficientes
Constantes Homogênea.
O PVI de segunda ordem é do tipo
{
y ′′ = f (t, y, y ′ )
y (t 0 ) = y 0 , y ′ (t 0 ) = y ′ 0
4.1 EDO’s de Segunda Ordem Lineares
Iremos admitir o seguinte Teorema de Existência e Unicidade:
Teorema: O PVI
{
y ′′ + p (t) y ′ + q (t) y = g (t)
y (t 0 ) = y 0 , y ′ (t 0 ) = y ′ 0
onde p, q e g são contínuas em um intervalo aberto t 0 ∈ I admite uma única
solução em I.
Teorema: Se y 1 e y 2 são soluções de
y ′′ + p (t) y ′ + q (t) y = 0
então qualquer combinação linear de y 1 e y 2 também é solução, isto é
αy 1 + βy 2 é solução, ∀α, β ∈ R.
Prova:
41

Temos que
y 1 ′′ + p (t) y 1 ′ + q (t) y 1 = 0
y 2 ′′ + p (t) y 2 ′ + q (t) y 2 = 0
Multiplicando a primeira equação por α, a segunda por β e somando obtemos
(αy 1 + βy 2 ) ′′ + p (t) (αy 1 + βy 2 ) ′ + q (t) (αy 1 + βy 2 ) = 0
e portanto segue o resultado.
Definição:
Um CONJUNTO FUNDAMENTAL DE SOLUÇÕES de soluções de
y ′′ + p (t) y ′ + q (t) y = 0
é um conjunto formado por duas soluções y 1 e y 2 e satisfazendo que qualquer
outra solução é uma combinação linear destas.
Definição:
a) f e g são LINEARMENTE INDEPENDENTES (LI) em I ⊂ R se
αf + βg = 0 ⇒ α = β = 0
b) f e g são LINEARMENTE DEPENDENTES (LD) em I ⊂ R se
∃α, β ∈ R, α 2 + β 2 ≠ 0tais que αf + βg = 0
Exemplos:
1)
são LI. De fato
f (t) = e t , g (t) = e 2t
αf + βg = 0 ⇒ αe t + βe 2t = 0, ∀t ∈ R ⇒
{ (fazendo t = 0) α + β = 0
⇒
(fazendo t = 1) α + eβ = 0 ⇒ α = β = 0
2)
são LD. De fato
e 2 ≠ 0, −1 ≠ 0.
f (t) = t, g (t) = 2t
2f − g = 0
Definição:
42

Dadas duas funções diferenciáveis f, g : I → R e t 0 ∈ I chamamos de
WRONSKIANO o determinante
W (f, g) (t 0 ) =
∣ f (t 0) g (t 0 )
f ′ (t 0 ) g ′ (t 0 ) ∣
Teorema (ABEL): Sejam y 1 e y 2 soluções de
y ′′ + p (t) y ′ + q (t) y = 0
onde p, q são funções contínuas em I ⊂ R. Temos:
a) Existe c ∈ R tal que
ou
b)
W (y 1 , y 2 ) (t) = ce − R p(t)dt .
W (y 1 , y 2 ) (t) ≠ 0, ∀t ∈ I
W (y 1 , y 2 ) (t) = 0, ∀t ∈ I.
Prova:
Como y 1 e y 2 são soluções da EDO temos
y 1 ′′ + p (t) y 1 ′ + q (t) y 1 = 0
y 2 ′′ + p (t) y 2 ′ + q (t) y 2 = 0
Multiplicando a primeira equação por (−y 2 ) , a segunda por (y 1 ) e somando
obtemos
(W (y 1 , y 2 ) (t)) ′ + p (t) W (y 1 , y 2 ) (t) = 0.
Assim W (y 1 , y 2 ) (t) é uma solução de
e portanto existe c ∈ R tal que
y ′ + p (t) y = 0
W (y 1 , y 2 ) (t) = ce − R p(t)dt .
b) É uma consequência direta de a).
Teorema:
Consideremos a EDO
y ′′ + p (t) y ′ + q (t) y = 0,
onde p, q são funções contínuas em I ⊂ R,e y 1 e y 2 duas soluções. São equivalentes:
43

a)
{y 1 , y 2 }
é um conjunto fundamental de soluções.
b)
{y 1 , y 2 }
é um conjunto LI.
c)
para algum t 0 ∈ I.
d)
W (y 1 , y 2 ) (t 0 ) ≠ 0
W (y 1 , y 2 ) (t) ≠ 0, ∀t ∈ I.
Prova:
O Teorema de Abel nos garante
c) ⇔ d)
c) ⇒ b)
Sejam y 1 e y 2 soluções satisfazendo que W (y 1 , y 2 ) (t 0 ) ≠ 0 para algum t 0 ∈ I.
Queremos provar que y 1 e y 2 são LI.
Suponhamos que
αy 1 + βy 2 = 0.
Assim α e β são soluções do sistema
{
y1 (t 0 ) α + y 2 (t 0 )β = 0
y ′ 1 (t 0 ) α + y ′ 2(t 0 )β = 0
Como o determinante da matriz dos coeficientes do sistema é não nulo, temos
que tal sistema admite somente a solução trivial. Logo
α = β = 0.
b) ⇒ d) :
Suponhamos que exista t 0 ∈ I tal que
W (y 1 , y 2 ) (t 0 ) = 0
Assim o sistema abaixo admite solução diferente da trivial
{
y1 (t 0 ) α + y 2 (t 0 )β = 0
y ′ 1 (t 0 ) α + y ′ 2(t 0 )β = 0
Seja
φ = αy 1 + βy 2
44

Observe que φ é uma solução da EDO que satisfaz
φ (0) = φ ′ (0) = 0
e portanto, pelo teorema de existência e unicidade
φ ≡ 0.
Assim
e isso é uma contradição.
αy 1 + βy 2 = 0
c) ⇒ a)
Queremos provar que
{y 1 , y 2 }
é um conjunto fundamental de soluções.
Seja φ uma solução da EDO. Queremos encontrar α, β ∈ R tais que
φ = αy 1 + βy 2 .
Como
W (y 1 , y 2 ) (t 0 ) ≠ 0
o sistema {
y1 (t 0 ) α + y 2 (t 0 )β = φ (t 0 )
y ′ 1 (t 0 ) α + y ′ 2(t 0 )β = φ ′ (t 0 )
admite uma solução α, β.
Daí, αy 1 + βy 2 é uma solução e
(αy 1 + βy 2 ) (t 0 ) = φ (t 0 )
(αy 1 + βy 2 ) ′ (t 0 ) = φ ′ (t 0 )
O Teorema de Existência e Unicidade garante que
φ = αy 1 + βy 2 .
a) ⇒ b) :
Observe que
V = {y|y ′′ + p (t) y ′ + q (t) y = 0}
é um espaço vetorial.
A afirmação a) nos diz que as funções y 1 e y 2 geram V. Se tais funções não
fossem LI então a dimensão de V seria menor que 2. Assim qualquer conjunto
formado por duas soluções seria LD e isso não é verdade. De fato, observe que
as soluções de { y ′′ + p (t) y ′ + q (t) y = 0
y (t 0 ) = 1, y ′ (t 0 ) = 0
45

e {
y ′′ + p (t) y ′ + q (t) y = 0
y (t 0 ) = 0, y ′ (t 0 ) = 1
denotadas respectivamente por φ e ψ são LI pois, como provamos c)⇒b), temos
W (φ, ψ) (t 0 ) =
∣ 1 0
0 1 ∣ = 1 ⇒ φ e ψ são LI
Exemplos:
1) y 1 = e t e y 2 = e −t formam um conjunto fundamental de soluções de
y ′′ − y = 0.
De fato, é trivial checarmos que y 1 e y 2 são soluções e como
∣ W (y 1 , y 2 ) (t) =
∣ et e −t ∣∣∣
e t −e −t = −2 ≠ 0
basta aplicarmos o teorema.
Assim a solução geral da equação é
y = ae t + be −t
Coloquemos uma condição inicial
{
y ′′ − y = 0
y (0) = 1, y ′ (0) = 0
Para encontrarmos a solução do PVI acima basta usarmos a solução geral e
as condições iniciais
y = ae t + be −t ⇒ 1 = a + b
y ′ = ae t − be −t ⇒ 0 = a − b
assim basta resolvermos o sistema
{ a + b = 1
a − b = 0
Portanto
a = b = 1 2
e a solução do PVI é
y = 1 2 et + 1 2 e−t = cosh t
46

2) y 1 = √ t e y 2 = 1 t
formam um conjunto fundamental de soluções de
2t 2 y ′′ + 3ty ′ − y = 0.
De fato, é trivial checarmos que y 1 e y 2 são soluções e como
√ ∣ W (y 1 , y 2 ) (t) =
t
1 ∣∣∣
t
∣
1
2 √ t
W (y 1 , y 2 ) (1) = − 3 2 ≠ 0
basta aplicarmos o teorema.
Assim a solução geral da equação é
− 1 t 2
EXERCÍCIOS:
y = a √ t + b 1 t
1) Determine o intervalo de maior amplitude dentro do qual o PVI proposto
tem, com certeza, uma solução única, duplamente derivável
{ (x − 3) y
a)
′′ + xy ′ + (ln |x|) y = 0
y (1) = 0, y ′ (1) = 1
{ (x − 2) y
b)
′′ + y ′ + (x − 2) (tan x) y = 0
y (3) = 1, y ′ (3) = 2
2) Verificar que
y 1 (t) = 1
e
y 2 (t) = √ t
são soluções da equação diferencial
yy ′′ + (y ′ ) 2 = 0
para t > 0. Depois mostrar que
a + b √ t
não é, em geral, solução desta equação. Por quê
3) É possível que y = sin ( t 2)
seja uma solução da equação
y ′′ + p (t) y ′ + q (t) y = 0
cujos coeficientes são contínuos, em um intervalo que contenha t = 0
47

4) Se y 1 e y 2 forem soluções LI de
ty ′′ + 2y ′ + te t y = 0
e se
achar o valor de
W (y 1 , y 2 ) (1) = 2
W (y 1 , y 2 ) (5) .
5) Se o wronskiano de duas soluções quaisquer de
y ′′ + p (t) y ′ + q (t) y = 0
é constante, o que se pode concluir sobre p e q
4.2 EDO’s Lineares Homogêneas de 2 a Ordem com Coeficientes
Constantes
Nesta seção estudaremos equações do tipo
ay ′′ + by ′ + cy = 0
Vamos aplicar a teoria da seção anterior.
Para encontrarmos um conjunto fundamental de soluções precisamos encontrar
duas candidatas a solução e em seguida verificarmos se de fato elas formam
um conjunto fundamental de soluções.
Buscamos soluções do tipo
y = e rt .
Temos
y ′ = re rt
y ′′ = r 2 e rt
e assim será possível encontrarmos uma solução como a pretendida se e somente
se
ar 2 e rt + bre rt + ce rt = 0 ⇔ ( ar 2 + br + c ) e rt = 0 ⇔ ar 2 + br + c = 0
A última equação é chamada de Equação Característica.
48

As raízes da equação característica podem ser
ou 2 reais distintas
ou 1 real dupla
ou 1 par complexo conjugado
1 o CASO: 2 REAIS DISTINTAS
Sejam
r 1 , r 2
as raízes reais e distintas da equação característica.
Afirmamos que
{e r1t , e r2t }
formam um conjunto fundamental de soluções. De fato
W ( ∣
e r1t , e r2t) (t) =
∣ er1t e r2t ∣∣∣
r 1 e r1t r 2 e r2t = (r 2 − r 1 ) e (r1+r1)t ≠ 0.
Exemplo:
Consideremos o PVI
⎧
⎨
⎩
y ′′ + 5y ′ + 6y = 0
y (0) = 2
y ′ (0) = 1 2
Inicialmente vamos encontrar a solução geral da EDO. Para isso vamos calcular
as raízes da equação característica
Assim
r 2 + 5r + 6 = 0 ⇔ r = −2 ou r = −3
{e −2t , e −3t }
forma um conjunto fundamental de soluções e portanto a solução geral é
y G = ae −2t + be −3t
Usando as condições iniciais temos
{
a + b = 2
−2a − 3b = 1 2
e assim
a = 13 2 , b = −9 2
49

Logo a solução do PVI é
y = 13 2 e−2t − 9 2 e−3t
Suponhamos que a equação característica
ar 2 + br + c = 0
admita apenas uma raiz real. Neste caso
e tal raiz é dada por
Assim sabemos que
∆ = b 2 − 4ac = 0
r = − b
2a
y 1 = e − b
2a t
é uma solução.
Precisamos encontrar uma segunda solução para montarmos um conjunto
fundamental de soluções e então obtermos uma solução geral.
Um método muito usual em EDO’s é tentar encontrar uma solução da forma
Neste caso temos
Assim
y 2 = v (t) e − b
2a t
y ′ 2 = − b
2a ve− b
2a t + v ′ e − b
2a t
y ′′
2 = b2
4a 2 ve− b
2a t − b a v′ e − b
2a t + v ′′ e − b
2a t
y 2 é solução ⇔
( b
2
⇔ a
4a 2 ve− b
2a t − b ) (
a v′ e − b
2a t + v ′′ e − b
2a t + b − b
)
2a ve− b
2a t + v ′ e − b
2a t + ve − b
2a t = 0 ⇔
⇔ − ∆ 4a v + av′′ = 0 ⇔ v ′′ = 0
Assim
serve.
Logo
também é solução.
v (t) = t
y 2 = te − b
2a t
50

Resta verificarmos que
{e − b
2a t , te − b
2a t }
forma um conjunto fundamental de soluções. De fato, temos
∣
(
W e − b
2a t , te − b t) e
2a (t) =
− b
2a t
te − b
2a t ∣∣∣∣ ∣ − b
2a e− b
2a t − b
2a te− b
2a t + e − b
2a t = e − b a t ≠ 0.
Exemplo:
Consideremos o PVI ⎧
⎨ y ′′ − y ′ + 1 4 y = 0
y (0) = 2
⎩
y ′ (0) = 1 3
Inicialmente vamos encontrar a solução geral da EDO. Para isso vamos calcular
as raízes da equação característica
Assim
r 2 − r + 1 4 = 0 ⇔ r = 1 2
{e 1 2 t , te 1 2 t }
forma um conjunto fundamental de soluções e portanto a solução geral é
y G = ae 1 2 t + bte 1 2 t
Usando as condições iniciais temos
{ a
2 + b = 1 3
a = 2
e assim
Logo a solução do PVI é
Sejam
a = 2, b = − 2 3
y = 2e 1 2 t − 2 3 te 1 2 t
λ + µi, λ − µi
as raízes da equação característica.
Observe que, se ignorarmos o fato de ainda não termos estudado funções de
variável complexa, uma solução seria
y = e (λ+µi)t
Assim
y = e λt e (µt)i
51

temos
Como
e αi =
+∞∑
n=0
(αi) n
=
n!
Assim temos que
e x = 1 + x + 1 2! x2 + 1 3! x3 + .. + xn
n! + ...
+∞∑
n=0
(−1) n α 2n +∞
(2n)! + ∑
(−1) n α 2n+1
= cos α + i sin α
(2n + 1)!
n=0
y 1 = e λt e µti = e λt (cos µt + i sin µt)
y 1 = e λt e −µti = e λt (cos µt − i sin µt)
são soluções da EDO.
Como a EDO é linear sabemos que a soma das duas soluções e que a diferença
das duas soluções também são soluções:
y 3 = 2e λt cos µt
y 4 = 2ie λt sin µt
Novamente por ser linear, se multiplicarmos a primeira por 1 2 e a segunda
por 1 2i ainda teremos duas soluções, que voltaremos a chamar de y 1 e y 2
y 1 = e λt cos µt
y 2 = e λt sin µt
Provemos que as duas funções acima formam um conjunto fundamental de
soluções
W ( e λt cos µt, e λt sin µt ) =
e λt cos µt e λt sin µt
∣ λe λt cos µt − µe λt sin µt µe λt cos µt + λe λt sin µt ∣ =
= µe 2λt ≠ 0.
Exemplo:
Consideremos o PVI
⎧
⎨
⎩
16y ′′ − 8y ′ + 145y = 0
y (0) = −2
y ′ (0) = 1
Inicialmente vamos encontrar a solução geral da EDO. Para isso vamos calcular
as raízes da equação característica
16r 2 − 8r + 145 = 0 ⇔ r = 1 4 ± 3i
Assim
{e 1 4 t cos 3t, e 1 4 t sin 3t}
52

forma um conjunto fundamental de soluções e portanto a solução geral é
y G = e 1 4 t (a cos 3t + b sin 3t)
Usando as condições iniciais temos
{
a = −2
a
4 + 3b = 1
e assim
Logo a solução do PVI é
EXERCÍCIOS:
a = −2, b = 1 2
y = e 1 4 t (
−2 cos 3t + 1 2 sin 3t )
1) Encontre a solução geral para a equação diferencial dada:
a)4y ′′ + y ′ = 0 f)2y ′′ − 5y ′ = 0
b)y ′′ − 36y = 0 g)y ′′ − 8y = 0
c)y ′′ + 9y = 0 h)3y ′′ + y = 0
d) d2 y
dx
+ 8 dy
2 dx + 16y = 0 i)y′′ − 3y ′ + 2y = 0
e)y ′′ + 3y ′ − 5y = 0 j)y ′′ + 4y ′ − y = 0
2) Resolva o PVI:
{
{
y
a)
′′ + y = 0
y ′ (0) = 0, y ( ) ′ π
b)
2 = 2
y ′′ − y = 0
y (0) = 1, y ′ (0) = 1
4.3 EDO’s Lineares de Segunda Ordem com Coeficientes
Constantes: O Método dos Coeficientes Indeterminados
——–
Nesta seção resolveremos EDO’s lineares de 2 a Ordem com coeficientes constantes
ay ′′ + by ′ + cy = g (t) (*)
Teorema: Consideremos a EDO (∗) onde g é uma função contínua em um
intervalo aberto I. Se y 1 e y 2 são soluções de (∗) então (y 1 − y 2 ) é uma solução
da homogênea associada
ay ′′ + by ′ + cy = 0.
53

Prova:
Como y 1 e y 2
são soluções de (∗) temos
ay 1 ′′ + by 1 ′ + cy 1 = g (t)
ay 2 ′′ + by 2 ′ + cy 2 = g (t)
e subtraindo a segunda equação da primeira obtemos
a (y 1 − y 2 ) ′′ + b (y 1 − y 2 ) ′ + c (y 1 − y 2 ) = 0
Logo (y 1 − y 2 ) é uma solução da homogênea associada.
Exercício: Verifique que o resultado continua valendo para EDO’s lineares,
não necessariamente com coeficientes constantes e não necessariamente de segunda
ordem.
Observação:
O teorema acima nos fornece o método para encontrarmos a solução geral
de uma EDO do tipo (∗) .
Sejam
y p
uma solução particular de (∗) , e
{y 1 , y 2 }
um conjunto fundamental de soluções da homogênea associada. Então qualquer
solução y de (∗) deve ser da forma
y = y p + ay 1 + by 2 .
De fato, se y é uma solução de (∗) então (y − y p ) é uma solução da homogênea
associada. Assim devem existir constantes a, b tais que
y − y p = ay 1 + by 2 .
PROBLEMA: Nosso problema agora será a obtenção de soluções particulares.
Vamos procurar soluções particulares conforme a tabela abaixo:
g (t)
y p
e αt At s e αt (s = 0, 1, 2)
poli de grau n t s . (poli de grau n) (s = 0, 1, 2)
e αt cos βt
Ae αt cos βt + Be αt sin βt
e αt sin βt
Ae αt cos βt + Be αt sin βt
(poli de grau n) .e αt (poli de grau n) .e αt
(poli de grau n) sin αt (poli de grau n) (sin αt + cos αt)
(poli de grau n) cos αt (poli de grau n) (sin αt + cos αt)
54

Exemplos:
1)
A homogênea associada
y ′′ − 3y ′ − 4y = 3e 2t
tem como solução geral
y ′′ − 3y ′ − 4y = 0
y h = ae 4t + be −t
Procuramos uma particular da forma
Temos
y p = Ae 2t
y ′ p = 2Ae 2t
y ′′
p = 4Ae 2t
Assim
e portanto
4Ae 2t − 6Ae 2t − 4Ae 2t = 3e 2t
A = − 1 2 .
Logo a solução geral é
y = − 1 2 e2t + ae 4t + be −t .
2)
A homogênea associada
y ′′ − 3y ′ − 4y = 2 sin t
tem como solução geral
y ′′ − 3y ′ − 4y = 0
y h = ae 4t + be −t
Procuramos uma particular da forma
Temos
y p = A sin t + B cos t
y p ′ = A cos t − B sin t
y p ′′ = −A sin t − B cos t
55

Assim
−A sin t − B cos t − 3A cos t + 3B sin t − 4A sin t − 4B cos t = 2 sin t
e portanto
Logo a solução geral é
(−5A + 3B) sin t + (−5B − 3A) cos t = 2 sin t
{ −5A + 3B = 2
−3A − 5B = 0
A = − 5
17 , B = 3 17
y = − 5
17 sin t + 3 17 cos t + ae4t + be −t .
3)
y ′′ − 3y ′ − 4y = −8e t cos 2t
A homogênea associada
y ′′ − 3y ′ − 4y = 0
tem como solução geral
y h = ae 4t + be −t
Procuramos uma particular da forma
Temos
Assim
y p = Ae t cos 2t + Be t sin 2t
y ′ p = (A + 2B) e t cos 2t + (−2A + B) e t sin 2t
y ′′
p = (−3A + 4B) e t cos 2t + (−4A − 3B) e t sin 2t
Logo a solução geral é
{ −10A − 2B = −8
2A − 10B = 0
A = 10
13 , B = 2
13
y = 10
13 et cos 2t + 2
13 et sin 2t + ae 4t + be −t .
4)
y ′′ − 3y ′ − 4y = 3e 2t + 2 sin t − 8e t cos 2t
56

A solução geral será da forma
onde
y = y h + y p1 + y p2 + y p3
são soluções particulares de
y p1
, y p2 , y p3
respectivamente.
Assim
5)
y ′′ − 3y ′ − 4y = 3e 2t ;
y ′′ − 3y ′ − 4y = 2 sin t;
y ′′ − 3y ′ − 4y = −8e t cos 2t
y = ae 4t + be −t − 1 2 e2t − 5
17 sin t + 3 10
cos t +
17 13 et cos 2t + 2
13 et sin 2t.
A homogênea associada
tem como solução geral
y ′′ + 4y = 3 cos 2t
y ′′ + 4y = 0
y h = a cos 2t + b sin 2t
Procuramos uma particular da forma
y p = At cos 2t + Bt sin 2t
Procuramos assim pois se não multiplicarmos por t será solução da homogênea.
Deixamos como exercício verificar que a solução geral é
y = a cos 2t + b sin 2t + 3 t sin 2t.
4
EXERCÍCIOS:
Resolva as equações diferenciais :
a)y ′′ + 3y ′ + 2y = 6 f)4y ′′ + 9y = 15
b)y ′′ − 10y ′ + 25y = 30x + 3 g)y ′′ + 4y = ( x 2 − 3 ) sin (2x)
c) 1 4 y′′ + y ′ + y = x 2 − 2x h)y ′′ + 2y ′ = 2x + 5 − e −2x
d)y ′′ + 3y = −48x 2 e 3x i)y ′′ − 16y = 2e 4x
e)y ′′ + 4y = 3 sin (2x) j)y ′′ + y = 2x sin x
57

4.4 EDO’s Lineares de Segunda Ordem com Coeficientes
Constantes: O Método da Variação dos Parâmetros
Nesta seção desenvovlvemos um método para obtermos soluções particulares.
Teorema: Se g é uma função contínua e se
{y 1 , y 2 }
é um conjunto fundamental de soluções de
y ′′ + by ′ + cy = 0
então
y p = −y 1
∫
gy 2
∣ y 1 y 2
y 1 ′ y 2
′
∫
+ y 2 ∣
gy 1
∣ y 1 y 2
y 1 ′ y 2
′
∣
é uma solução particular de
y ′′ + by ′ + cy = g (t)
temos
Prova:
Procurando uma solução particular do tipo
y p = u 1 y 1 + u 2 y 2
y ′ p = u 1 y ′ 1 + u 2 y ′ 2 + (u ′ 1y 1 + u ′ 2y 2 )
e por um motivo técnico vamos exigir que a parte entre parênteses seja nula.
Assim
Substituindo na equação obtemos
y p ′ = u 1 y 1 ′ + u 2 y 2
′
y p ′′ = u 1 y 1 ′′ + u ′ 1y 1 ′ + u 2 y 2 ′′ + u ′ 2y 2
′
u 1 (y ′′
1 + by ′ 1 + cy 1 ) + u 2 (y ′′
2 + by ′ 2 + cy 2 ) + u ′ 1y ′ 1 + u ′ 2y ′ 2 = g
e como as partes nos parênteses são nulas, já que y 1 e y 2 são soluções da homogênea,
temos { u
′
1 y 1 + u ′ 2y 2 = 0
u ′ 1y ′ 1 + u ′ 2y ′ 2 = g
Para o sistema acima ter solução basta que
∣ y 1 y 2
y 1 ′ y 2
′ ∣ ≠ 0
58

e isso é verdade já que y 1 e y 2 formam um conjunto fundamental de soluções da
homogênea.
Aplicando a regra de Cramer temos
∣ 0 y 2
u ′ g y 2
′ ∣ gy
1 =
∣ y 1 y 2
= −
2
y 1 ′ y 2
′ ∣ ∣ y 1 y 2
y 1 ′ y 2
′ ∣
e
Logo
∣ y 1 0
u ′ y 1
′ g ∣ gy
2 =
∣ y 1 y 2
=
1
y 1 ′ y 2
′ ∣ ∣ y 1 y 2
y 1 ′ y 2
′ ∣
∫
gy 2
u 1 = −
∣ y 1 y 2
y 1 ′ y 2
′ ∣
∫
gy 1
u 2 =
∣ y 1 y 2
y 1 ′ y 2
′ ∣
Exercício: Verifique que o resultado continua valendo para EDO’s lineares,
não necessariamente com coeficientes constantes.
Exemplo:
Vamos encontrar a solução geral de
A homogênea associada é
que tem solução
y ′′ + 4y = 3 csc t
y ′′ + 4y = 0
y h = a cos 2t + b sin 2t
Utilizando o método da variação dos parâmetros obtemos
cos 2t sin 2t
∣ −2 sin 2t 2 cos 2t ∣ = 2
∫
cos 2t
y p = −
2
3 csc t sin 2tdt +
sin 2t
2
∫
3 csc t cos 2tdt =
= −3 sin t cos 2t + 3 sin 2t cos t + 3 sin 2t ln |csc t − cot t|
2
59

A solução geral é
y = a cos 2t + b sin 2t − 3 sin t cos 2t + 3 sin 2t cos t + 3 sin 2t ln |csc t − cot t| .
2
EXERCÍCIOS:
Resolva as equações, usando o método da variação dos parâmetros
a)y ′′ + y = sec x
b)y ′′ + y = sin x
c)y ′′ + y = cos 2 x
d)y ′′ − y = cosh x
e)y ′′ − 9y = 9x
e 3x
f)y ′′ − 2y ′ + y = e −x ln x
4.5 EDO’s Lineares de Segunda Ordem com Coeficientes
Variáveis: Soluções dadas por Séries de Potências
Nesta seção iremos estudar EDO’s da forma
P (x) y ′′ + Q (x) y ′ + R (x) y = 0.
As equações mais famosas que possuem a forma acima são as equações da
Física-Matemática
a) BESSEL : x 2 y ′′ + xy ′ + ( x 2 − ν 2) y = 0
b) LEGENDRE :
(
1 − x
2 ) y ′′ − 2xy ′ + α (α + 1) y = 0
c) HERMITE : y ′′ − 2xy ′ + λy = 0
d) EULER-CAUCHY : x 2 y ′′ + αxy ′ + βy = 0
4.5.1 Soluções em Vizinhanças de Pontos Ordinários
Consideremos a EDO
Usaremos a notação
P (x) y ′′ + Q (x) y ′ + R (x) y = 0
p (x) = Q (x)
P (x)
q (x) = R (x)
P (x)
60

Definição:Dizemos que x 0 é um PONTO ORDINÁRIO se p e q forem
analíticas em x 0 . Caso contrário x 0 é dito PONTO SINGULAR.
Exemplos:
1)
Todos os pontos são ordinários.
y ′′ + y = 0
2)
Assim
x 2 y ′′ + xy ′ = 0
y ′′ + 1 x y′ = 0
e x 0 = 0 é um ponto singular.
3) (
1 − x
2 ) y ′′ − 2xy ′ + x 2 y = 0
Assim
y ′′ −
e x 0 = 1 e x 0 = −1 são pontos singulares.
2x
1 − x 2 y′ + x2
1 − x 2 y = 0
Observação: Se P, Q, R são polinômios então p e q são analíticas em x 0
desde que
P (x 0 ) ≠ 0.
Teorema:
Se x 0 for um ponto ordinário da EDO
y ′′ + p (x) y ′ + q (x) y = 0
podemos sempre encontrar duas soluções LI na forma de série de potências
centradas em x 0
+∞∑
y = c n (x − x 0 ) n .
n=0
Além disso as séries convergem para uma solução em
|x − x 0 | < R
onde R é a menor distância entre x 0 e os pontos singulares de p e q.
Prova: Omitida.
Exemplos:
61

1) Consideremos a EDO
y ′′ + y = 0
Não existem pontos singulares. Assim o teorema garante que existem soluções
da forma
convergentes em (−∞, +∞) .
Temos
y =
+∞∑
n=0
a n x n
y ′ =
y ′′ =
+∞∑
n=1
+∞∑
na n x n−1
n (n − 1) a n x n−2 =
+∞∑
n=2
n=0
(n + 2) (n + 1) a n+2 x n
Assim
e portanto
+∞∑
n=0
(n + 2) (n + 1) a n+2 x n +
+∞∑
n=0
+∞∑
n=0
a n x n = 0
[(n + 2) (n + 1) a n+2 + a n ] x n = 0
Observe que
Temos
e portanto
(n + 2) (n + 1) a n+2 + a n = 0, ∀n ∈ N
a n
a n+2 = −
(n + 2) (n + 1)
a 0 = y (0)
a 1 = y ′ (0)
a 2 = − a 0
2 , a 4 = a 0
4.3.2 , ..., a 2n = (−1) n a 0
(2n)!
a 3 = − a 1
3.2 , a 5 = a 1
5.4.3.2 , ..., a 2n+1 = (−1) n a 1
(2n + 1)!
∑
+∞
y = a 0 (−1) n x 2n
(2n)! + a 1
n=0
+∞∑
n=0
(−1) n x 2n+1
(2n + 1)! = a 0 cos x + a 1 sin x
62

2)Consideremos a EDO
y ′′ − xy = 0
Não existem pontos singulares. Assim o teorema garante que existem soluções
da forma
convergentes em (−∞, +∞) .
Temos
y =
+∞∑
n=0
a n x n
y ′ =
y ′′ =
+∞∑
n=1
+∞∑
na n x n−1
n (n − 1) a n x n−2 =
+∞∑
n=2
n=0
(n + 2) (n + 1) a n+2 x n
Assim
logo
+∞∑
n=0
⇒ 2a 2 +
Temos então
(n + 2) (n + 1) a n+2 x n −
+∞∑
⇒ 2a 2 +
n=1
+∞∑
+∞∑
n=0
(n + 2) (n + 1) a n+2 x n −
n=1
a n x n+1 = 0 ⇒
+∞∑
n=1
a n−1 x n = 0 ⇒
[(n + 2) (n + 1) a n+2 − a n−1 ] x n = 0
a 2 = a 5 = a 8 = ... = 0
a n−1
a n+2 =
(n + 2) (n + 1)
a 3n =
a 3n+1 =
y = a 0
(
1 + 1
3.2 x3 + 1
6.5.3.2 x6 + ...
a 0
(3n) (3n − 1) (3n − 3) (3n − 4) ...6.5.3.2
a 1
(3n + 1) (3n) (3n − 2) (3n − 3) ...7.6.4.3
)
+ a 1
(
x + 1
4.3 x4 + 1 )
7.6.4.3 x7 + ....
Chamando
y 1 = 1 + 1
3.2 x3 + 1
6.5.3.2 x6 + ...
y 2 = x + 1
4.3 x4 + 1
7.6.4.3 x7 + ....
63

temos que y 1 e y 2 são soluções dos PVI’S
{
y ′′ − xy = 0
y (0) = 1, y ′ (0) = 0
{
y ′′ − xy = 0
y (0) = 0, y ′ (0) = 1
respectivamente.
3) A EDO (
x 2 − 2x + 2 ) y ′′ + y ′ = 0
tem como pontos singulares
1 + i, 1 − i
Assim
x 0 = 0
é um ponto ordinário e podemos garantir a existência de uma solução na forma
y =
convergente em ( − √ 2, √ 2 ) .
+∞∑
n=0
a n x n
4) A EDO (
1 − x
2 ) y ′′ − 2xy ′ + y = 0
tem como pontos singulares
1, −1
Assim
x 0 = 0
é um ponto ordinário e podemos garantir a existência de uma solução na forma
y =
convergente em (−1, 1) .
+∞∑
n=0
a n x n
5) A EDO
(1 + x 2 )y ′′ + 2xy ′ + 4x 2 y = 0
tem como pontos singulares
i, −i
64

Assim
x 0 = 1 2
é um ponto ordinário e podemos garantir a existência de uma solução na forma
convergente em
EXERCÍCIOS:
y =
+∞∑
n=0
(
1
2 − √ 5
2 , 1 2 + √ )
5
2
.
(
a n x − 1 ) n
2
1) Encontre solução em série de potências:
a) y ′′ − y = 0, x 0 = 0
b) y ′′ − xy ′ − y = 0, x 0 = 0
c) y ′′ − xy ′ − y = 0, x 0 = 1
2) Use um computador para plotar diversas somas parciais da solução em
série em torno de 0 { y ′′ − xy ′ − y = 0
y (0) = 1, y ′ (0) = 0
3) Calcule as 4 primeiras derivadas da solução de:
a) { y ′′ + xy ′ + y = 0
y (0) = 1, y ′ (0) = 0
b) { y ′′ + (sin x) y ′ + (cos x) y = 0
y (0) = 0, y ′ (0) = 1
4.5.2 Pontos Singulares Regulares e a Equação de Euler
Dada a EDO
vimos que x 0 é um ponto singular se
P (x) y ′′ + Q (x) y ′ + R (x) y = 0
ou
não são analíticas em x 0 .
p (x) = Q (x)
P (x)
q (x) = R (x)
P (x)
65

Definição: x 0 é dito PONTO SINGULAR REGULAR se
i) x 0 for um ponto singular e
ii) (x − x 0 ) p (x) e (x − x 0 ) 2 q (x) são analíticas em x 0 .
Exemplos:
1) (
1 − x
2 ) y ′′ − 2xy ′ + y = 0
tem como pontos singulares
Como
1, −1.
2x
(x − 1) p (x) =
x + 1
(x − 1) 2 q (x) = 1 − x
1 + x
são analíticas em 1 segue que 1 é ponto singular regular.
Analogamente verificamos que −1 também é ponto singular regular.
2)
tem como pontos singulares
Como
2 (x − 2) 2 xy ′′ + 3xy ′ + (x − 2) y = 0
xp (x) =
x 2 q (x) =
0, 2
3x
2 (x − 2) 2
x (x − 2)
2 (x − 2) 2
são analíticas em 0 segue que 0 é ponto singular regular.
Como
3
(x − 2) p (x) =
2 (x − 2)
não é analítica em 2 segue que 2 não é ponto singular regular.
A
EQUAÇÃO DE EULER
66

A Equação de Euler é a seguinte equação
Inicialmente observemos que
x 2 y ′′ + αxy ′ + βy = 0.
x 0 = 0
é um ponto singular regular da EDO. Assim não esperamos encontrar uma
solução definida em um intervalo contendo a origem. Uma boa esperança é que
tenhamos soluções definidas em x > 0 ou em x < 0.
Busquemos uma solução do tipo
Assim
y = x r
y ′ = rx r−1
y ′′ = r (r − 1) x r−2
r (r − 1) x r + αrx r + βx r = 0
[r (r − 1) + αr + β] x r = 0
Verificamos que isso é possível desde que
r (r − 1) + αr + β = 0
(EQUAÇÃO CARACTERÍSTICA)
temos
Ou seja
Denotando
√
r = (1 − α) ± (α − 1) 2 − 4β
.
2
∆ = (α − 1) 2 − 4β
1 o Caso: ∆ > 0
Neste caso existem r 1 , r 2 raízes distintas e assim
são soluções e como
temos que
y 1 = x r1
y 2 = x r2
W (y 1 , y 2 ) (x) = x r1+r2−1 (r 2 − r 1 ) ≠ 0
{x r1 , x r2 }
formam um conjunto fundamental de soluções.
67

2 o Caso: ∆ = 0
Neste caso temos que a equação característica tem uma raiz real dupla
Assim
r = 1 − α
2
y 1 = x r
é uma solução.
Buscamos uma segunda solução na forma
Temos
y ′ 2 = rux r−1 + u ′ x r
y 2 = ux r
y ′′
2 = r (r − 1) ux r−2 + ru ′ x r−1 + u ′′ x r + ru ′ x r−1
e substituindo na equação obtemos
e portanto
(r (r − 1) + αr + β) ux r + (2r + α) u ′ x r+1 + u ′′ x r+2 = 0
u ′ x r+1 + u ′′ x r+2 = 0
u ′ + u ′′ x = 0
Fazendo
obtemos
v = u ′
xv ′ + v = 0
x dv
dx = −v
− dv
v
= dx x
− ln v = ln x
v = 1 x
u = ln x
Logo
é a segunda solução.
Como
y 2 = (ln x) x r
W (y 1 , y 2 ) (x) = x 2r−1 ≠ 0
68

segue as soluções formam um conjunto fundamental.
3 o Caso: ∆ < 0
Neste caso temos que a equação característica possui um par complexo conjugado
de raízes
λ + µi, λ − µi
Assim temos
x λ+µi = x λ x µi = x λ e ln xµi = x λ e (µ ln x)i =
As nossas duas soluções serão
= x λ (cos (µ ln x) + i sin (µ ln x))
y 1 = x λ cos (µ ln x)
y 2 = x λ sin (µ ln x)
Deixamos como exercício a verificação de que as duas funções acima formam
um conjunto fundamental de soluções.
Exemplo:
2x 2 y ′′ + 3xy ′ − y = 0, x > 0
A equação caracteristica é
2r 2 + r − 1 = 0
cujas raízes são
Logo
1
2 , −1
y 1 = √ x
y 2 = 1 x
EXERCÍCIOS:
1) Determinar os pontos singulares e verificar se são regulares ou não:
a)xy ′′ + (1 − x) y ′ + xy = 0 d)xy ′′ − 3 (sin x) y ′ + ( 1 + x 2) y = 0
b) (x + 3) y ′′ − 2xy ′ + ( 1 − x 2) y = 0 e) (sin x) y ′′ + xy ′ + 4y = 0
c) ( x 2 + x − 2 ) y ′′ + (x + 1) y ′ + 2y = 0 f) (x sin x) y ′′ + 3y ′ + xy = 0
2) Resolva as equações:
a)x 2 y ′′ + 4xy ′ + 2y = 0 c)x 2 y ′′ − 3xy ′ + 4y = 0
b) (x + 1) 2 y ′′ + 3 (x + 1) y ′ + 0.75y = 0 d)x 2 y ′′ + 3xy ′ + 5y = 0
69

4.5.3 Soluções em Vizinhanças de Pontos Singulares Regulares
——–
Suponhamos que x 0 seja um ponto singular regular de
y ′′ + p (x) y ′ + q (x) y = 0
Assim
xp (x) =
x 2 q (x) =
∞∑
p n x n
n=0
∞∑
q n x n
n=0
Multipliquemos a equação por x 2
x 2 y ′′ + x [xp (x)] y ′ + [ x 2 q (x) ] y = 0
e vamos procurar uma solução da forma
y = x r
∞
∑
n=0
a n x n
Substituindo na equação obtemos
(
∞∑
∞
) (
∑
∞
)
∑
(n + r) (n + r − 1) a n x n+r + p n x n (n + r) a n x n+r +
n=0
n=0
n=0
( ∞
) (
∑
∞
)
∑
+ q n x n a n x n+r = 0
n=0
n=0
Efetuando os produtos acima obtemos
a 0 F (r) x r +
F (r) = r (r − 1) + rp 0 + q 0
[
]
∞∑
n−1
∑
a n F (r + n) + a k ((k + r)p n−k + q n−k ) x n+r = 0
n=0
Assim procuramos
k=0
F (r) = 0(Lembre da Equação de Euler)
n−1
∑
a n F (r + n) + a k ((k + r)p n−k + q n−k ) = 0
k=0
Ou seja , procuramos soluções da forma
y = x r (a 0 +
70
∞∑
a n x n )
n=1

onde r é raiz de
r (r − 1) + rp 0 + q 0 = 0.
Para sermos mais precisos deveríamos agora fazer uma analíse das raízes da
equação acima. No entanto vamos parar nossa discussão por aqui.
Exemplo:
Consideremos a EDO
Os únicos pontos singulares são
2x (x + 1) y ′′ + (3 + x) y ′ − xy = 0
0, −1
Então para x 0 ∈ R\{0, −1} encontramos soluções definidas em vizinhanças
de x 0 da forma
∞∑
y = a n (x − x 0 ) n
n=0
Verifique que x 0 = 0 é um ponto singular regular com p 0 = 3 2 e q 0 = 0.
Assim obtemos a equação
r (r − 1) + 3 2 r = 0
cujas raízes são 0 e − 1 2 .
Assim podemos procurar soluções da forma
)
∞∑
∞∑
y 1 = x
(a 0 0 + a n x n = a 0 + a n x n
y 2 =
1
√ x
(b 0 +
n=1
)
∞∑
b n x n
n=1
n=1
Verifique agora que x 0 = −1 é um ponto singular regular
q 0 = 0. Assim obtemos a equação
com p 0 = −1 e
r (r − 1) − r = 0
cujas raízes são 0 e 2.
Como as raízes diferem por um número inteiro podemos encontrar somente
uma solução que será da forma
)
∞∑
y = (x + 1)
(a 2 0 + a n x n
n=1
71

5 A Transformada de Laplace
5.1 Preliminares
Definição: Seja f uma função definida em (0, +∞) . A TRANSFORMADA
DE LAPLACE de f é definida por
L (f) (s) =
caso a integral seja convergente.
∫ +∞
0
e −st f (t) dt,
Exemplo:
Consideremos
Temos
f (t) = e kt , k ∈ R.
L (f) (s) =
∫ +∞
0
= lim
T →+∞
e −st e kt dt =
e (k−s)t ] T
k − s
0
∫ +∞
0
= 1
s − k
e (k−s)t dt =
para s > k.
Definição: Uma função
f : [a, b) → R
é dita SECCIONALMENTE CONTÍNUA se existem
a = t 0 < t 1 < ... < t n−1 < t n = b
tais que f é contínua em (t i , t i+1 ) , i = 0, 1, ..., n − 1.
Definição: Dizemos que
f : [a, +∞) → R
é SECCIONALMENTE CONTÍNUA se a restrição de f a [a, b), qualquer que
seja b > a, for seccionalmente contínua.
Teorema: Seja
f : [a, +∞) → R
72

seccionalmente contínua. Suponhamos que
tais que
a)
b)
∃M > 0, ∃g : [M, +∞) → R
|f (x)| < g (x) , ∀x ≥ M;
∫ +∞
é convergente.
Então ∫ +∞
é convergente.
Prova: Omitida (Curso de Análise)
M
a
g (x) dx
f (x) dx
Teorema: Se f for seccionalmente contínua para t ≥ 0 e se existirem
constantes k > 0, M > 0 e a ∈ R tais que
então L (f) (s) converge para s > a.
|f (t)| < ke at , ∀t ≥ M
Prova: Basta aplicar o teorema anterior para
g (t) = ke at
TABELA BÁSICA
f (t)
L (f) (s)
1
1
s , s > 0
e at 1
s−a , s > a
t n n!
, n ∈ N
s
, s > 0
n+1
a
sin at
s 2 +a
, s > 0
2
s
cos at
s 2 +a
, s > 0
2
a
sinh at
s 2 −a
, s > |a|
2
s
cosh at
s 2 −a
, s > |a|
2
e at b
sin bt
, s > a
(s−a) 2 +b 2
e at s−a
cos bt
, s > a
(s−a) 2 +b 2
t n e at n!
, n ∈ N , s > a
(s−a) n+1
73

PROPRIEDADES DA TRANSFORMADA DE LAPLACE
a)
L (af + bg) (s) = aL (f) (s) + bL (g) (s)
b) Se f for contínua , f ′ seccionalmente contínua e existirem constantes
k, a, M tais que
|f (t)| ≤ ke at , ∀t ≥ M
então existe L (f ′ ) (s) para s > a e
c)
L (f ′ ) (s) = sL (f) (s) − f (0)
L (f ′′ ) (s) = s 2 L (f) (s) − sf (0) − f ′ (0)
d)
(
L f (n)) (s) = s n L (f) (s)−s n−1 f (0)−s n−2 f ′ (0)−...−sf (n−2) (0)−f (n−1) (0)
A verificação das propriedades acima é imediata. Basta usar a definição e
efetuar o cálculo.
5.2 Utilização da Transformada de Laplace na Resolução
de PVI’s
Exemplos:
1) Consideremos o PVI
{ y ′′ + y = sin 2t
y (0) = 2, y ′ (0) = 1
Denotemos
Assim
L (y) (s) = Y (s)
L (y ′′ ) (s) = s 2 Y (s) − sy (0) − y ′ (0) = s 2 Y (s) − 2s − 1
L (sin 2t) (s) = 2
s 2 + 4
Temos então
s 2 Y (s) − 2s − 1 + Y (s) = 2
s 2 + 4
74

e portanto
e decompondo em frações parciais
Y (s) = 2s3 + s 2 + 8s + 6
(s 2 + 1) (s 2 + 4)
Y (s) = 5 1
3 s 2 + 1 + 2 s
s 2 + 1 − 2 1
3 (s 2 + 4)
Calculando a transformada inversa
y (t) = 5 3 sin t + 2 cos t − 2 sin 2t
3
2) Consideremos o PVI
{
y (4) − y = 0
y (0) = 0, y ′ (0) = 1, y ′′ (0) = 0, y ′′′ (0) = 0
Denotemos
L (y) (s) = Y (s)
Assim
(
L y (4)) (s) = s 4 Y (s) − s 3 y (0) − s 2 y ′ (0) − y ′′′ (0) = s 4 Y (s) − s 2
Temos então
e portanto
s 4 Y (s) − s 2 − Y (s) = 0
Y (s) =
Calculando a transformada inversa
EXERCÍCIOS
s2
s 4 − 1 = 1
4 (s − 1) − 1
4 (s + 1) + 1
2 (s 2 + 1)
y (t) = 1 4 et − 1 4 e−t + 1 2
sin t =
sin t + sinh t
2
Use a transformada de Laplace para resolver os seguintes PVI’s
{ y
a)
′′ − y ′ − 6y = 0
{ y (0) = 1, y ′ (0) = −1
y
b)
′′ + 3y ′ + 2y = 0
y (0) = 1, y ′ (0) = 0
{ y
c)
′′ − 2y ′ + 2y = 0
{ y (0) = 0, y ′ (0) = 1
y
d)
′′ − 4y ′ + 4y = 0
y (0) = 1, y ′ (0) = 1
75

5.3 Aplicação: PVI’s com Dados Descontínuos
Definição: A função
dada por
é chamada de Função Degrau.
u c (t) =
u c : R → R
{
0 se t < c
1 se t ≥ c
Exemplo:
Podemos expressar a função dada por
⎧
⎨ 0 se 0 ≤ t < π
h (t) = 1 se π ≤ t < 2π
⎩
0 se t ≥ 2π
utilizando a função degrau
h (t) = u π (t) − u 2π (t)
Proposição
a)
b)
c)
L (u c ) (s) = e−cs
s , s > 0
L (u c (t) f (t − c)) (s) = e −cs L (f) (s)
F (s) = L (f) (s) , s > a ≥ 0 ⇒ L −1 ( e −cs F (s) ) (t) = u c (t) f (t − c)
d)
F (s) = L (f) (s) , s > a ≥ 0 ⇒ L ( e ct f (t) ) (s) = F (s − a)
e)
F (s) = L (f) (s) , s > a ≥ 0 ⇒ L −1 (F (s − a)) = e ct f (t)
Prova:
Basta efetuar o cálculo.
Exemplos:
1) Vamos calcular a transformada de
{
sin t, 0 ≤ t < π
f (t) =
4
sin t + cos ( )
t − π 4 , t ≥
π
4
76

Inicialmente observamos que
e aplicando as propriedades obtemos
f (t) = sin t + u π
4 (t) cos (t − π 4
L (f) (s) = 1
s 2 + 1 + e− π 4 s s
s 2 + 1
)
2) Calculemos a transformada inversa de
Temos
F (s) = 1 − e−2s
s 2
F (s) = 1 s 2 − e−2s 1 s 2
e assim
onde
Assim
L −1 (F (s)) (t) = t − u 2 (t) f (t − 2)
f (t) = L −1 ( 1
s 2 )
= t
L −1 (F (s)) (t) = t − u 2 (t) (t − 2)
3) Calculemos a transformada inversa de
onde
Temos
Assim
G (s) =
1
s 2 − 4s + 5
1
G (s) =
(s − 2) 2 = F (s − 2)
+ 1
F (s) = 1
s 2 + 1
L −1 (G (s)) (t) = L −1 (F (s − 2)) (t) = e ct L −1 (F (s)) = e 2t sin t
4) Vamos resolver o PVI
{ 2y ′′ + y ′ + 2y = u 5 (t) − u 20 (t)
y (0) = y ′ (0) = 0
77

Usando transformada temos
Y (s) = L (y (t)) (s)
2s 2 Y (s) + sY (s) + 2Y (s) = e−5s
− e−20s
s s
Y (s) =
e−5s − e −20s
s (2s 2 + s + 2) = ( e −5s − e −20s) 1 1
s 2s 2 + s + 2
Denotamos
H (s) = 1 1
1
s 2s 2 + s + 2 = 2
s − 1 ( )
s +
1
4
( )
2 s +
1 2
− 1 1
4
(
4 +
15 2
16 s +
1
4
[
1
h (t) = L −1 2
s − 1 ( )
]
s +
1
4
( )
2 s +
1 2
− 1 1
4
( )
4 +
15 2
16 s +
1 2
=
4 +
15
16
Assim
= 1 2 − e − t 4 cos
2
( √15
4 t )
−
e − t 4 sin
( √15
4 t )
2 √ 15
.
) 2
+
15
16
y (t) = L −1 [( e −5s − e −20s) H (s) ] = u 5 (t) h (t − 5) − u 20 (t) h (t − 20) .
6 Sistemas de Equações Diferenciais Ordinárias
no Plano
6.1 Introdução
Um sistema de Equações Diferenciais Ordinárias no plano é um sistema da
forma { x ′ = f(x, y, t)
y ′ = g(x, y, t)
onde f, g estão definidas em algum subconjunto U ⊂ R 3 .
Uma solução de um sistema como acima é uma curva diferenciável
α : I ⊂ R → R 2 dada por α(t) = (x(t), y(t)) satisfazendo
x ′ (t) = f(x(t), y(t), t) e y ′ (t) = g(x(t), y(t), t)
O estudo clássico de EDO’s propunha resolver explicitamente as equações e
ao longo dos séculos, foi desenvolvida uma quantidade enorme de técnicas para
78

esolver vários tipos de EDO’s. É interessante lembrar, por exemplo, que a
função exponencial nasceu como solução do PC (Problema de Cauchy)
{ ẋ = x
x (0) = 1 .
Teorias desenvolvidas para resolver algumas equações, como a da Transformada
Integral, em particular a Transformada de Laplace, traduzem a EDO em
uma equação algébrica: se esta for solúvel então a Transformada Integral Inversa
produz as soluções da EDO. Abel (1802-1829), por exemplo, entre tantas outras
coisas, trabalhou em tais transformadas; acontece que se a equação algébrica
resultante da transformada for de grau maior ou igual a 5, Abel mostrou que
não se pode encontrar soluções explícitas por meio de radicais, o que invalida
o ataque. Inúmeros casos de EDO’s continuam sendo estudados até hoje, mas
foi POINCARÉ (1854-1912) que unificou enormemente a teoria das EDO’s, desenvolvendo
o que se passou a denominar a Teoria Qualitativa. O problema
de Poincaré era que para as EDO’s da Mecânica Celeste que estudadava, os
métodos quantitativos não eram suficientes sequer para começar o estudo. O
que Poincaré detectou é que, se por um lado a quantidade de EDO’s que se
pode resolver no sentido estrito é relativamente pequeno, por outro lado, em
compensação, com novos conceitos de análise, geometria e topologia, pode-se
resolver uma equação no sentido qualitativo; ou seja entender as leis gerais de
comportamento das soluções, mesmo quando estas não são obtidas explicitamente.
A partir de Poincaré, Liapunov e Birkhoff, a Teoria Qualitativa dos Sistemas
Dinâmicos tem ocupado a atenção de inúmeros matemáticos. Mas foi em anos
recentes que ela teve suas metas gerais estabelecidas, tomou forma e experimentou
um desenvolvimento marcante. Mais de duas décadas se passaram entre dois
pólos importantes: o trabalho de Andronov e Pontryagin (1937), introduzindo
o conceito básico de estabilidade estrutural, e os trabalhos de Peixoto (1958-
1962), provando a densidade de campos de vetores estáveis em superfícies. Foi
então que Smale enriqueceu substancialmente a teoria , definindo, como objetivo
central, a busca de propriedades genéricas e estáveis, obtendo resultados
e propondo problemas da maior relevância. Nesta mesma época , Hartman
e Grobman mostraram que a estabilidade local é uma propriedade genérica.
Logo a seguir , Kupka e Smale atacaram, com sucesso, o problema para órbitas
periódicas.
Definição: Um sistema de Equações Diferenciais Ordinárias no plano é
dito AUTÔNOMO quando for do tipo
{ x ′ = f(x, y)
y ′ (*)
= g(x, y)
onde f, g estão definidas em um subconjunto U ⊂ R 2 .
79

{
x
Exemplo:
′ = sin(x) + 2y
y ′ = x 2 + y 3
é autônomo.
Neste curso vamos estudar sistemas do tipo (*) com f, g ∈ C 1 em um
aberto U ⊂ R 2 . Uma solução de (*) é uma curva α : I ⊂ R → R 2 dada por
α(t) = (x(t), y(t)) satisfazendo
x ′ (t) = f(x(t), y(t)) e y ′ (t) = g(x(t), y(t)).
Observe que (f(x, y), g(x, y)) é o vetor velocidade da curva α em (x, y). De
fato, sendo α(t) = (x(t), y(t)) temos que
(f(x(t), y(t)), g(x(t), y(t))) = (x ′ (t), y ′ (t)) = α ′ (t).
Assim o par (f, g) define um campo de vetores.
{ x
Exemplo:
′ = 2x
y ′ = −y
As soluções são curvas que apresentam vetores tangentes como acima. Por
exemplo, α(t) = (exp(2t), exp(−t)) é uma solução que passa pelo ponto (1, 1)
quando t = 0. Note também que α(t) = (− exp(2t), exp(−t)) é uma solução que
passa por (−1, 1) quando t = 0.
Definição: Um PROBLEMA DE VALOR INICIAL (PVI) é um sistema
(∗) acompanhado de uma condição inicial : x(t 0 ) = x 0 , y(t 0 ) = y 0 .
Observe que no exemplo temos que fixado um ponto do plano existe uma
única curva que é solução do sistema e que passa por este ponto. Dizemos que
uma solução do PVI é uma ”trajetória” ou ”órbita” que em tempo t 0 passa
por (x 0 , y 0 ).
É fácil vermos que o traço da curva que passa por (x 0 , y 0 ) no tempo t 0 é
o mesmo que o da curva que passa por (x 0 , y 0 ) em um tempo t 1 . Desta forma
vamos considerar somente PVI’s com condição inicial
x(0) = x 0 , y(0) = y 0 . (**)
Teorema (Existência e Unicidade): Suponhamos que f, g ∈ C 1 em
U ⊂ R 2 aberto. Então, para qualquer (x 0 , y 0 ) ∈ U, existe uma única curva
α : I → R 2 , onde I é um intervalo contendo 0, dada por α(t) = (x(t), y(t))
satisfazendo (*) e (**).
Não iremos demonstrar este teorema neste curso.
80

Definição: O retrato de fase do sistema (*) é a união de todos os traços
das trajetórias deste sistema.
Definição:Uma singularidade de (*) é um ponto que satisfaz
f(x, y) = g(x, y) = 0.
Exemplos: { x
1)
′ = 2x
y ′ apresenta como soluções α(t) = (x
= −y
0 e 2t , y 0 e −t ).
singularidade do sistema é o ponto (0, 0).
A única
2)
{ x ′ = αx
y ′ = βy
apresenta como soluções α(t) = (x 0 e αt , y 0 e βt ).
i) α = 0, β > 0 ou α = 0, β < 0 : Neste caso o eixo 0X é composto de
singularidades do sistema.
ii)α > 0, β = 0 ou α < 0, β = 0 : Neste caso o eixo 0Y é composto de
singularidades.
iii) α = β > 0 ou α > β > 0 ou 0 < α < β : Neste caso a origem (0, 0)
é a única singularidade. O primeiro é conhecido como FONTE e os seguintes
NÓS REPULSORES. Se α > β > 0 as trajetórias (exceto as que possuem traço
contido no eixo 0X) tangenciam o eixo 0Y e se 0 < α < β as trajetórias (exceto
as que possuem traço contido no eixo 0Y ) tangenciam o eixo 0X.
iv) α = β < 0 ou α < β < 0 ou β < α < 0 : Neste caso a origem (0, 0)
é a única singularidade. O primeiro é conhecido como POÇO e os seguintes
NÓS ATRATORES. Se α < β < 0 as trajetórias (exceto as que possuem traço
contido no eixo 0X) tangenciam o eixo 0Y e se β < α < 0 as trajetórias (exceto
as que possuem traço contido no eixo 0Y ) tangenciam o eixo 0X.
v) β < 0 < α ou α < 0 < β : Neste caso a origem (0, 0) é a única
singularidade. Este caso é conhecido como SELA. No primeiro caso as trajetórias
aproximam-se do eixo 0Y quando o parâmetro t aproxima-se de −∞ e
aproximam-se do eixo 0X quando o parâmetro t aproxima-se de +∞; no segundo
caso as trajetórias aproximam-se do eixo 0X quando o parâmetro t aproxima-se
de −∞ e aproximam-se do eixo 0Y quando o parâmetro t aproxima-se de +∞.
81

{
x
3)
′ = y
y ′ = 8xy
. Temos que
x ′ = y, y ′ = 8xy ⇒ y′ dy
= 8x ⇒
x
′
dx = 8x ⇒ y = 4x2 + C
Assim as trajetórias possuem seus traços contidos nos gráficos das funções
da família acima. Além disso é fácil verificar que o eixo 0X é composto de
singularidades.
Definição (FLUXO OU SISTEMA DINÂMICO): Uma família de
funções
ϕ t : R 2 → R 2 , t ∈ R
satisfazendo
a) ϕ t é contínua,
b) ϕ 0 = id,
c) ϕ t+s = ϕ t ◦ ϕ s
é um FLUXO ou SISTEMA DINÂMICO no plano.
Exemplo: Suponhamos que as soluções de
{
x ′ = f(x, y)
y ′ = g(x, y)
(*)
estejam globalmente definidas.
Seja ϕ a aplicação
ϕ : R 2 × R → R 2
(P, t) ↦→ ϕ(P, t) = (x(t), y(t))
onde (x(t), y(t)) é a solução de (∗) satisfazendo (x(0), y(0)) = P. É fácil verificar
que a família ϕ t dada por ϕ t (P ) = ϕ(P, t) satisfaz a definição de fluxo.
6.2 Sistemas de EDO’S Lineares no Plano
——-
{ x
Um sistema de edo’s lineares no plano é um sistema da forma
′ = ax + by
y ′ = cx + dy ,
com x(0) = x 0 , y(0) = y 0 onde a, b, c, d ∈ R. Para simplificarmos a notação representaremos
estes sistemas na forma matricial:
[ ] [ ]
x a b
X = A = X ′ =
y c d
X ′ = AX, X(0) =
[
x0
y 0
]
[ x
′
y ′ ]
(∗)
82

Nosso objetivo é estudar todos os tipos de sistemas lineares no plano. Para
isto é necessário que façamos uma classificação das matrizes 2 × 2. O polinômio
característico de A é o polinômio dado por
p(λ) =
∣ a − λ b
c d − λ ∣ = λ2 − (trA)λ + det A.
Assim as soluções de p(λ) = 0 podem ser: duas raízes reais e distintintas:
λ 1 , λ 2 ; uma raiz real dupla: λ; ou um par complexo conjugado: α + iβ, α − iβ.
No primeiro caso dizemos que λ 1 , λ 2 são auto-valores e podemos encontrar
uma base B do plano formada por auto-vetores de tal forma que
[ ]
λ1 0
[A] B
=
.
0 λ 2
No segundo caso temos duas possibilidades. Se a multiplicidade geométrica
de λ for igual a 2 então podemos encontrar uma base B do plano formada por
auto-vetores de tal forma que
[A] B
=
[ λ 0
0 λ
Se a multiplicidade geométrica de λ for igual a 1 então podemos encontrar uma
base B do plano formada por auto-vetores de tal forma que
[ ] λ 1
[A] B
= .
0 λ
No terceiro caso encontramos um vetor de C 2 satisfazendo A(u + iv) =
(α + iβ)(u + iv). Além disso B = {u, v} é uma base do plano satisfazendo
[ ] α −β
[A] B
=
.
β α
]
.
Considere o sistema (*). Temos:
[ ]
λ1 0
i) Se [A] =
então a solução de (*) é dada por (x(t), y(t)) =
0 λ 2
= (x 0 e λ1t , y 0 e λ2t ). Na seção anterior já esboçamos os possíveis retratos de fase.
[ ] λ 1
ii) Se [A] =
então a solução de (*) é dada por (x(t), y(t)) =
0 λ
= ((x 0 + y 0 t)e λt , y 0 e λt ).
Se λ < 0 , a única singularidade (0, 0) é chamada de NÓ IMPRÓPRIO
ATRATOR:
83

Se λ > 0 , a única singularidade (0, 0) é chamada de NÓ IMPRÓPRIO
REPULSOR:
[ ] α −β
iii) Vamos analisar o caso A =
.
β α
Vamos utilizar coordenadas polares para encontrarmos explicitamente as
soluções. Começamos com a mudança x = r cos θ e y = r sin θ .
As condições iniciais r 0 , θ 0 serão dadas por x 0 = r 0 cos θ 0 e y 0 = r 0 sin θ 0 .
Assim temos
x = r cos θ ⇒ x ′ = r ′ cos θ − rθ ′ sin θ (1)
y = r sin θ ⇒ y ′ = r ′ sin θ + rθ ′ cos θ
Multiplicando a primeira linha por (cos θ) e a segunda por (sin θ) e em
seguida somando as duas linhas obtemos
x ′ cos θ + y ′ sin θ = r ′ (**)
Multiplicando a primeira linha por (− sin θ) e a segunda por (cos θ) e em
seguida somando as duas linhas obtemos
Substituindo (*) em (**) e em (***) obtemos
{ r ′ = αr
θ ′ = β .
A solução do sistema acima é dada por
Voltando para x, y temos
−x ′ sin θ + y ′ cos θ = rθ ′ (***)
r = r 0 e αt
θ = θ 0 + βt
x(t) = e αt (x 0 cos βt − y 0 sin βt)
y(t) = e αt (y 0 cos βt + x 0 sin βt)
Se α = 0 a singularidade (0, 0) é chamada de CENTRO. Se β > 0 o campo
de vetores é do tipo
Note que a diferença entre este e o de cima está na orientação.
Se α > 0 a singularidade (0, 0) é chamada de FOCO REPULSOR, no sentido
anti-horário se β > 0 e no sentido horário se β < 0.
Se β > 0 o campo de vetores é do tipo
84

Se β < 0 o campo de vetores é do tipo
Se α < 0 a singularidade (0, 0) é chamada de FOCO ATRATOR, no sentido
anti-horário se β > 0 e no sentido horário se β < 0.
Se β > 0 o campo de vetores é do tipo
Se β < 0 então o campo de vetores é do tipo
Observe que o sinal de α determina se a singularidade é atratora ou repulsora.
Já o sinal de β está relacionado com o sentido da rotação.
Exemplos onde A não está na forma canônica:
1) Considere o seguinte sistema
[ ]
X ′ 1 −1
=
X.
−2 0
Seu polinômio característico é dado por p(λ) = λ 2 − λ − 2 , e as raízes
deste polinômio são 2 e −1. Os auto-vetores associados aos auto-valores são
respectivamente (1, −1) e (1, 2).
Consideramos a base formada por estes auto-vetores: B = {(1, −1), (1, 2)}.
Temos então
[ ]
[ ]
[ ]
y1
x1
Y = = P X = P , P −1 1 1
=
y 2 x 2 −1 2
[
Y ′ = P X ′ = P
Assim
1 −1
−2 0
]
X = P
[
1 −1
−2 0
(y 1 (t), y 2 (t)) = (ae 2t , be −t )
]
P −1 Y =
(x 1 (t), x 2 (t)) = (ae 2t + b −t , −ae 2t + 2be −t ).
2) Considere o seguinte sistema
X ′ =
[ 0 −2
1 2
]
X.
[ 2 0
0 −1
Seu polinômio característico é dado por p(λ) = λ 2 − 2λ + 2 e as raízes deste
polinômio são 1 + i e 1 − i. O auto-vetor complexo associado ao auto-valor 1 + i
é (1 + i, −i).
Consideramos a base formada pelas partes real e imaginária: B = {(1, 0), (1, −1)}.
Temos então
[
y1
]
Y = = P X = P
y 2
[
Y ′ = P X ′ 0 −2
= P
1 2
[
x1
]
x 2
]
X = P
[ ]
, P −1 1 1
=
0 −1
[ ] 0 −2
P −1 Y =
1 2
[ 1 −1
1 1
]
Y
]
Y.
85

Logo
(y 1 (t), y 2 (t)) = (ae t cos t − be t sin t, be t cos t + ae t sin t)
(x 1 (t), x 2 (t)) = ((a + b)e t cos t + (a − b)e t sin t, −be t cos t − ae t sin t).
Dado um sistema linear
X ′ = AX
podemos classificar a singularidade (0, 0) a partir do polinômio característico de
A.
p(λ) = λ 2 − (tra A)λ + det A
∆ = (tra A) 2 − 4 det A
∆ det tra (0, 0)
> 0 < 0 ∈ R SELA
> 0 > 0 < 0 NÓ AT RAT OR
> 0 > 0 > 0 NÓ REP ULSOR
< 0 ∈ R = 0 CENT RO
< 0 ∈ R < 0 F OCO AT RAT OR
< 0 ∈ R > 0 F OCO REP ULSOR
= 0 ∈ R > 0 NÓ REP ULSOR
= 0 ∈ R < 0 NÓ AT RAT OR
6.3 Noções de Estabilidade Local
Conside o sistema de EDO’s
{ x ′ = f(x, y)
y ′ = g(x, y)
(*)
onde f, g ∈ C 1 em um aberto U ⊂ R 2 .
Definição: Uma singularidade (x 1 , y 1 ) de (*) é dita:
a) ESTÁVEL se (∀ε > 0, ∃δ > 0)tal que
(||(x(0), y(0)) − (x 1 , y 1 )|| < δ ⇒ ||(x(t), y(t)) − (x 1 , y 1 )|| < ε, ∀t > 0)
b) INSTÁVEL se não for estável.
c) ASSINTOTICAMENTE ESTÁVEL se
∃ε > 0tal que
(||(x(0), y(0)) − (x 1 , y 1 )|| < ε ⇒ lim
t→+∞ (x(t), y(t)) = (x 1, y 1 ))
86

d) ASSINTOTICAMENTE INSTÁVEL se
∃ε > 0tal que
(||(x(0), y(0)) − (x 1 , y 1 )|| < ε ⇒ lim
t→−∞ (x(t), y(t)) = (x 1, y 1 ))
Exemplos:
{ x
1) A singularidade (0, 0) de
′ = 2x
y ′ = −4y é instável.
{ x
2) A singularidade (0, 0) de
′ = −y
y ′ é estável.
{
= x
x
3) A singularidade (0, 0) de
′ = −x − y
y ′ é assintoticamente estável.
{
= x − y
x
4) A singularidade (0, 0) de
′ = x − y
y ′ é assintoticamente instável.
{
= x + y
x
5)A singularidade (0, 0) de
′ = −2x
y ′ é assintoticamente estável.
= −y
Observação:
Dado o campo de vetores linear
X ′ = AX
temos que :
a) A singularidade (0, 0) é assintoticamente estável se e somente se os autovalores
de A tiverem partes reais negativas.
b) A singularidade (0, 0) é assintoticamente instável se e somente se os autovalores
de A tiverem partes reais positivas.
6.4 Sistemas de EDO’s não Lineares no Plano
Nesta seção vamos dar uma pequena noção do comportamento qualitativo
de alguns sistemas de edo’s não lineares no plano.
Definição: Dois campos vetoriais X, Y definidos em abertos U e V de R 2 ,
respectivamente, são ditos TOPOLOGICAMENTE EQUIVALENTES quando
existe um homeomorfismo h : U → V que leva órbitas de X em órbitas de Y
preservando a orientação.
Observações:
1) Se a aplicação h da definição acima for de classe C r dizemos que X e Y
são C r −EQUIVALENTES.
2) Denotando ϕ e ψ os fluxos de X e Y, respectivamente, dizemos que h é
uma CONJUGAÇÃO TOPOLÓGICA se h(ϕ(t, x, y)) = ψ(t, h(x, y)).
3) Se a aplicação h de 2) for de classe C r dizemos que X e Y são C r −CONJUGADOS.
87

Exemplo: Consideremos os campos de vetores dados por X = (x, −y) e
Y = (x, −y + x 3 )
Seus fluxos são dados respectivamente por ϕ(t, x, y) = (xe t , ye −t ) e ψ(t, x, y)
= (xe t , (y − x3
4 )e−t + x3
4 e3t ) .
A aplicação h : R 2 → R 2 dada por h(x, y) = (x, y + x3
4
) define uma
C r −Conjugação.
Teorema do Fluxo Tubular: Sejam X : U → R 2 , U ⊂ R 2 aberto e p ∈ U
um ponto regular de X ∈ C k . Então existe um difeomorfismo de classe C k que
conjuga X em uma vizinhança de p com o campo constante Y = (1, 0) restrito
a uma vizinhança da origem (0, 0).
Demonstração: Daremos apenas uma idéia de como construir o difeomorfismo
. Como p é um ponto regular existe uma seção transversal ao campo por
p isto é, existe uma aplicação
satisfazendo
A difeomorfismo será dado por
ξ : (−δ, δ) → R 2
ξ (0) = p
Iξ ′ (s) ⊕ X (ξ (s)) = R 2 , ∀s ∈ (−δ, δ) .
h (t, s) = ϕ(t, ξ (s)).
Definição: Um ponto singular p de um campo vetorial X = (f, g) de classe
C 1 chama-se HIPERBÓLICO se os auto-valores de
[ ∂f
∂x
JX(p) =
(p) ∂f
∂y (p)
]
∂g
∂x (p) ∂g
∂y (p)
tem parte real diferente de zero.
É imediato verificarmos que (0, 0) é uma singularidade hiperbólica do campo
linear X ′ = AX se e somente se os auto-valores de A tem parte real não nula.
Como vimos anteriormente, as fontes, os poços, os nós , as selas e os focos
são hiperbólicos. Já o centro nos fornece um exemplo de singularidade não
hiperbólica.
Uma singularidade não deixa de ser hiperbólica se perturbarmos ligeiramente
o campo de vetores. O mesmo não ocorre com o centro, como vimos com o
exemplo
X(x, y) = (−x −
X(0, 0) = (0, 0)
y
ln √ (x 2 + y 2 ) , −y + x
ln √ (x 2 + y 2 ) )
88

Note que a parte linear na origem é um centro e no entanto a origem é um
foco do sistema acima.
Teorema de Grobman & Hartman : Sejam X = (f, g) : U → R 2 ,
U ⊂ R 2 aberto , um campo vetorial de classe C 1 e p ∈ U um ponto singular
hiperbólico. Existem vizinhanças V de p em U e W de (0, 0) em R 2 tais que
X|V é topologicamente conjugado a JX(p) restrito a W.
Exemplos:
⎧
⎨ x ′ = −x −
1) Consideremos o seguinte sistema
⎩ y ′ = −y +
√ y
ln (x 2 +y 2 )
√ x
ln (x 2 +y 2 )
Vamos utilizar coordenadas polares para entender seu retrato de fase:
x = r cos θ
y = r sin θ
Assim temos
r ′ cos θ − r sin θθ ′ = x ′ = −r cos θ − r sin θ
ln r
r ′ sin θ + r cos θθ ′ = y ′ = −r sin θ + r cos θ
ln r
Multiplicando a primeira equação por (cos θ) e a segunda por (sin θ) e finalmente
somando as duas obtemos
r ′ = −r.
Multiplicando a primeira equação por (− sin θ) e a segunda por (cos θ) e
finalmente somando as duas obtemos
rθ ′ =
θ ′ =
r
ln r
1
ln r
e assim nosso sistema fica
{ r ′ = −r
θ ′ = 1
ln r
e temos
r(t) = c exp(−t), c > 0
θ ′ (t) =
1
ln c − t
Claramente vemos que o retrato de fase apresenta um foco atrator com
sentido horário na origem. Note que a parte linear do sistema apresenta um nó
atrator na origem.
89

{ x
2) Consideremos o seguinte sistema
′ = −y − x √ (x 2 + y 2 )
y ′ = x − y √ (x 2 + y 2 )
coordenadas polares temos
. Utilizando
r ′ cos θ − r sin θθ ′ = x ′ = −r sin θ − r 2 cos θ
r ′ sin θ + r cos θθ ′ = y ′ = r cos θ − r 2 sin θ
r ′ = −r 2
rθ ′ = r
e assim nosso sistema fica { r ′ = −r 2
θ ′ = 1
Assim
r(t) = 1 , θ(t) = t + θ 0
t + c
Claramente vemos que o retrato de fase apresenta um foco atrator com
sentido anti-horário na origem. Note que a parte linear do sistema apresenta
um centro na origem.
3) ( O Pêndulo Simples sem Atrito)
Consideremos um corpo de massa m preso na haste de um pêndulo.
Suponhamos que a haste tenha comprimento l. Vamos descrever o movimento
do corpo em cima da circunferência de raio l. Se o ângulo que a haste faz
com a posição de equilíbrio é θ então o comprimento de circunferência percorrido
é
s (t) = lθ (t)
A aceleração será dada por
s ′′ (t) = lθ ′′ (t)
Vamos supor que a única força que atua no corpo seja a componente tangencial
da gravidade g:
F (s, s ′ ) = −mg sin s l
Assim temos, pela segunda Lei de Newton
mlθ ′′ = −mg sin θ
e portanto a equação diferencial que descreve o movimento do corpo é
θ ′′ + g l
sin θ = 0.
Fazendo
obtemos o sistema
x = θ, y = θ ′
{
x ′ = y
y ′ = − g l sin θ .
90

Os pontos singulares do campo de vetores são (kπ, 0) , k ∈ Z.
A matriz jacobiana de X é dada por
[ ]
0 1
JX(x, y) =
− g l
0
Para (x, y) = (kπ, 0) , k ∈ Z, par, a singularidade (0, 0) é um centro da
jacobiana e para k ímpar a singularidade (0, 0) será uma sela.
Para visualizarmos o retrato de fase dividimos y ′ por x ′ e obtemos
dy
dx = − g l sin x
y
e assim concluímos que as soluções estão contidas nas curvas de nível de
V (x, y) = y2
2 − g l cos x
Teorema: Seja p um ponto singular isolado de um campo de vetores X ∈
C 1 . Se os auto-valores de JX(p) têm partes reais negativas então p é uma
singularidade assintoticamente estável e se houver um auto-valor com parte real
positiva então p é um ponto singular instável.
Exemplos:
1) Utilizando o teorema acima podemos classificar as singularidades de
X (x, y) = ( x 2 + y 2 − 6, x 2 − y ) .
Temos que os pontos singulares são (√ 2, 2 ) e ( − √ 2, 2 ) . Temos
(√ )
JX 2, 2
(
JX − √ )
2, 2
=
=
[ √ ]
2 2 4
2 √ 2 −1
[ √ ]
−2 2 4
−2 √ 2 −1
Como o determinante da primeira é negativo então JX (√ 2, 2 ) tem um autovalor
positivo e portanto a singularidade (√ 2, 2 ) é instável. Como o determinante
da segunda é positivo e o traço é negativo então JX (√ 2, 2 ) tem ambos
auto-valores com partes reais negativas e portanto a singularidade ( − √ 2, 2 ) é
assintoticamente estável.
2) Seja X : R 2 → R 2 o campo definido por
X (x, y) = ( −x, −y 3) .
Observe que a origem é a única singularidade de X e obtemos uma boa idéia
de como deve ser o retrato de fase.
A origem parece ser assintoticamente estável mas o teorema anterior permanece
mudo a respeito já que
91

[
−1 0
JX (0, 0) =
0 0
]
.
Como provar que a origem é de fato assintoticamente estável
6.5 Funções de Lyapounov
Definição: Sejam X : U → R 2 um campo e V : U 0 → R uma função
diferenciável. Para cada x ∈ U ∩ U 0 definimos a derivada de V na direção de
X por
V X ′ (x) = V ′ (x) .X (x) = 〈gradV (x) , X (x)〉.
Definição: Sejam X : U → R n um campo de classe C 1 no aberto U ⊆ R n
com uma singularidade p ∈ U e V : U 0 → R uma função qualquer.
Dizemos que V é uma FUNÇÃO DE LYAPOUNOV para X em p se e
somente se:
a) p ∈ U 0 ∩ U e V é diferenciável no aberto U 0 ⊆ R n ;
b) Para todo x ∈ U 0 tem-se V (x) ≥ 0 com V (x) = 0 se e somente se x = p;
c) Para todo x ∈ U 0 tem-se V X ′ (x) ≤ 0.
Dizemos que V é uma FUNÇÃO DE LYAPOUNOV ESTRITA para X em
p se e somente se V é uma FUNÇÃO DE LYAPOUNOV para X em p e
∀x ∈ U ∩ U 0 : V ′ X (x) = 0 ⇔ x = p.
Teorema: Seja X : U → R 2 um campo de classe C 1 no aberto U ⊆ R 2
com uma singularidade p ∈ U.
a) Se existe uma FL para X em p então p é uma singularidade estável de
X.
b) Se existe uma FLE para X em p então p é uma singularidade assintoticamente
estável de X.
Exemplo: Seja
X (x, y) = ( −x − xy 2 , −xy 2 − y 3) .
É fácil verificar que a origem é a única singularidade de X. Como
[ ] −1 0
JX (0, 0) =
0 0
o primeiro teorema não se aplica.
92

É fácil verificar que
V (x, y) = x2 + y 2
2
é uma FLE para X em (0, 0) . Logo (0, 0) é uma singularidade assintoticamente
estável.
Corolário: Seja X : U → R 2 um campo de classe C 1 no aberto U ⊆ R 2
com uma singularidade p ∈ U. Suponhamos que V : U 0 → R é uma FL para X
em p tal que o conjunto
Z = {z ∈ U ∩ U 0 |V ′ X (z) = 0}
não contém nenhuma órbita positiva de X, exceto p, então p é uma singularidade
assintoticamente estável.
Exemplo: Seja
X (x, y) = ( y − x 3 , −x 3) .
É fácil verificar que
V (x, y) = x 4 + 2y 2
é uma FL que não é FLE. Porém o corolário acima garante que (0, 0) é uma
singularidade assintoticamente estável.
6.6 Conjuntos Limites e o Teorema de Poincaré-Bendixon
{ x
Consideremos um sistema de edo’s no plano
′ = f(x, y)
y ′ = g(x, y)
de classe C 1 em U ⊂ R 2 aberto.
Dizemos que Q ∈ ϖ(P ) ( Q está no ϖ-limite de P ) se
onde f, g são
∃t n → +∞ tal que ϕ(P, t n ) → Q
onde ϕ(P, t n ) denota o fluxo .
Dizemos que Q ∈ α(P ) ( Q está no α-limite de P ) se
∃t n → −∞ tal que ϕ(P, t n ) → Q.
Na verdade o ϖ-limite e o α-limite dependem da órbita γ que passa por P.
Assim mudaremos nossa notação para ϖ(γ) e α(γ).
Exemplos:
1) Considere a órbita γ do exemplo 1 da seção anterior:
γ = {(0, 0)} ⇒ ϖ(γ) = α(γ) = {(0, 0)}
γ ≠ {(0, 0)} ⇒ ϖ(γ) = {(0, 0)} e α(γ) = ∅
93

{
x
2) Considere o seguinte sistema linear
′ = x
y ′ = −y
. Temos:
ϖ(1, 0) = ∅, α(1, 0) = {(0, 0)}
ϖ(0, 1) = {(0, 0)}, α(0, 1) = ∅
Algumas Propriedades:
Se a semi-órbita positiva γ + (P ) é limitada então:
conexo e invariante isto é
ϖ(γ) ≠ ∅, é compacto;
Q ∈ ϖ(γ) ⇒ ϕ(Q, t) ∈ ϖ(γ)
Propriedades semelhante são satisfeitas pelo α−limite.
Teorema (Poincaré-Bendixon): Se a semi-órbita positiva é limitada e o
ϖ-limite não contém singularidades então ele é uma órbita periódica ( isto é, é
o traço de uma curva fechada).
Não iremos provar o teorema mas iremos dar um exemplo de aplicação.
Ressaltamos também que este teorema somente é válido no plano. Indicamos
[S 2 ].
Exemplo: Considere a seguinte edo de 2 a ordem
x ′′ + (2x 2 + (x ′ ) 2 − 2)x ′ + x = 0.
Observemos que esta equação sequer é linear. No entanto somos capazes de
provar que existe uma solução periódica. Começamos transformando a equação
em um sistema:
y = x ′
y ′ = x ′′ = −(2x 2 + y 2 − 2)y − x
{ x ′ = y
y ′ = −(2x 2 + y 2 − 2)y − x .
Vamos provar que existe uma órbita periódica no anel Ω = {(x, y)|1 <
x 2 + y 2 < 3}.
A única singularidade do sistema é (0, 0). Assim em Ω não temos singularidades.
Vamos provar que o anel é invariante pelo fluxo do sistema. Temos
Assim temos
d
dt (x2 + y 2 ) = −2y 2 (2x 2 + y 2 − 2) (*)
x 2 + y 2 = 3 ⇒ ∗ < 0
x 2 + y 2 = 1 ⇒ ∗ > 0
94

Logo, considerando P ∈ Ω, pelo Teorema de Poincaré-Bendixon, ϖ(P ) é
uma órbita periódica.
Exercícios
1) Faça um esboço do comportamento dos seguintes campos lineares
a) [ 1
]
2
2
b) [ −2
2
]
c) [ 0 1
0 0
d) [ 1
2
−2
2 0
e) [ 0 1
1 0
f) [ −1 −1
1 −1
]
]
]
]
g) ⎡
⎣ 1
−1
0
⎤
⎦
h) ⎡
⎣
1
−2
2
⎤
⎦
i) ⎡
⎣ 0
−1
0
⎤
⎦
j) ⎡
⎣ −1 −1
1 −1
1
⎤
⎦
95

2) Faça um esboço do comportamento dos seguintes campos polinomiais:
a)X (x, y) = ( −x 2 , −2y 2) d)X (x, y) = ( −4x 3 + 6x 2 − 2x, −2y )
b)X (x, y) = ( x 2 − y 2 , 2xy ) e)X (x, y) = ( x, −y + x 3)
c)X (x, y) = ( x, x 3)
3) Obtenha explicitamente a trajetória maximal de X : R n → R n por x 0 ∈
R n e t 0 ∈ R arbitrários, nos seguintes casos:
a)n = 1 e X (x) = x 2 d)n = 2 e X (x, y) = (2x, y)
b)n = 2 e X (x, y) = (−y, x) e)n = 2 e X (x, y) = ( x 2 , 2y )
c)n = 2 e X (x, y) = (−x, y) f)n = 3 e X (x, y, z) = ( −y, x, − 1 2 z)
4) Escreva a EDO de segunda ordem como sistema autônomo plano e ache
todos os pontos singulares:
a)x ′′ + 9 sin x = 0 d)x ′′ + (x ′ ) 2 + 2x = 0
b)x ′′ + x ′ (1 − x 3 ) − x 2 = 0 e)x ′′ + 4x
1+x
+ 2x ′ = 0
2
c)x ′′ + x = εx 3 , ε > 0
5) Encontre as trajetórias e esboce o retrato de fase dos seguintes campos
lineares:
[ ] 1 2
a)
4 3
[ ] −4 2
b)
− 5 2
2
[ ] 10 −5
c)
8 −12
[ ] 0 2
d)
8 0
[ 1
]
e) 2
9
1
f)
2
2
[ −6 2
−3 1
6) Usando coordenadas polares encontre as trajetórias dos campos dados,
passando pelos pontos dados. Descreva o comportamento geométrico.
(
a)X (x, y) = −y − x ( x 2 + y 2) 2 (
, x − y x 2 + y 2) ) 2
, p = (4, 0)
b)X (x, y) = ( y + x ( x 2 + y 2) , −x + y ( x 2 + y 2)) , p = (4, 0)
c)X (x, y) = ( −y + x ( 1 − x 2 − y 2) , x + y ( 1 − x 2 − y 2)) , p = (1, 0)
(
x (
d)X (x, y) = y − √ 4 − x 2 − y 2) y (
, −x − √ 4 − x 2 − y 2)) ,
x2 + y 2 x2 + y 2
p = (1, 0) e p = (2, 0)
]
96

7) Classifique a singularidade (0, 0) dos campos:
[ ] [ ]
−5 3
−5 3
a)
d)
[
2 7
] [
2 −7
]
−5 3
−5 3
b)
e)
[
−2 5
] [
−7 4
]
−
3 1
3 1
c) 2 4
−1 − 1 g) 2 4
1
2
−1
2
8) Estabeleça condições sobre a constante µ de modo que (0, 0) seja um
centro [ ] −µ 1
.
−1 µ
9) Estabeleça condições sobre a constante µ de modo que (0, 0) seja um foco
atrator [
0 1
]
−1 µ
10) Prove que (0, 0) é sempre uma singularidade repulsora de
[
µ
]
1
−1 1
onde µ é uma constante real e µ ≠ 1. Quando é que (0, 0) é um ponto de sela
E foco repulsor
11) Seja γ = γ (t) uma trajetória do campo linear
[ ]
α −β
β
α
passando por um ponto p 0 . Estabeleça condições sobre α e β que garantam que
lim γ (t) = 0
t→+∞
12) Prove que (0, 0) é uma singularidade atratora do campo
X (x, y) = ( αx − βy + y 2 , βx + αy − xy ) .
13) Classifique as singularidades dos campos:
a)X (x, y) = (1 − 2xy, 2xy − y) e)X (x, y) = ( x 2 − y 2 − 1, 2y )
b)X (x, y) = ( y − x 2 + 2, x 2 − xy ) f)X (x, y) = ( 2x − y 2 , −y + xy )
c)X (x, y) = ( −3x + y 2 + 2, x 2 − y 2) g)X (x, y) = ( xy − 3y − 4, y 2 − x 2)
d)X (x, y) = ( −2xy, y − x + xy − y 3)
14) Prove que a equação diferencial não linear de 2 a ordem
(
1 + α 2 x 2) x ′′ +
(
β 2 + (x ′ ) 2) x = 0
97

tem um ponto de sela em (0, 0) , quando β < 0.
15) Prove que o campo de vetores
X (x, y) = ( −αx + xy, 1 − βy − x 2)
tem uma única singularidade quando αβ > 1 e que essa singularidade é atratora
quando β > 0.
16) Prove que a solução do PVI
{ x ′′ + 2x − x 2 = 0
x (0) = 1, x ′ (0) = 0
é periódica.
17) O sistema {
x ′ = 3 ( x + y − 1 3 x3 − k )
y ′ = − 1 3
(x + 0.8y − 0.7)
é um caso especial das equações de Fitzhugh-Nagumo, que modelam a transmissão
de impulsos nervosos ao longo de um axônio. O parâmetro k é o estímulo
externo.
a) Para k = 0, mostre que existe apenas um ponto singular. Determine-o
e mostre que se trata de um foco atrator. Repita a análise para k = 0.5 e
mostre que a singularidade agora é um foco repulsor. Desenhe retratos de fase
do sistema para os dois valores de k.
b) Determine o valor k 0 para o qual a singularidade muda de atratora para
repulsora. Desenhe o retrato de fase do sistema para o valor k 0 .
c) Mostre que para k ≥ k 0 o sistema admite uma órbita periódica.
d) Verifique que a órbita periódica existe para uma faixa de valores de k
menores que k 0 . Determine o menor valor de k para o qual existe uma órbita
periódica.
18)
a)Utilizando o Teorema de Green prove que se U 0 ⊆ U é um aberto simplesmente
conexo e tal que div (X) não é identicamente nulo e nem troca de sinal
em U 0 então X não possui órbita periódica inteiramente contida em U 0 .
b) Prove que
X (x, y) = ( y − x 3 , −x 3)
não possui órbita periódica alguma. Esboce o retrato de fase e verifique que a
não existência de órbitas periódicas não é óbvia.
19) Verifique se a origem é uma singularidade estável ou até assintoticamente
estável de cada um dos campos seguintes:
a)X (x, y) = ( −2x − y 2 , −y − x 2)
b)X (x, y) = ( −x − 2y 2 , −y 3 + xy )
c)X (x, y) =
(−x + 2x (x + y) 2 , −y 3 + 2y 3 (x + y) 2)
d)X (x, y) = ( y − xy 2 , x 3)
e)X (x, y) = ( x 3 − x − y, x )
(
f)X (x, y) = −x − x3
3
− 2 sin y, −y −
y3
3
)
98