Funções reais de variável rea

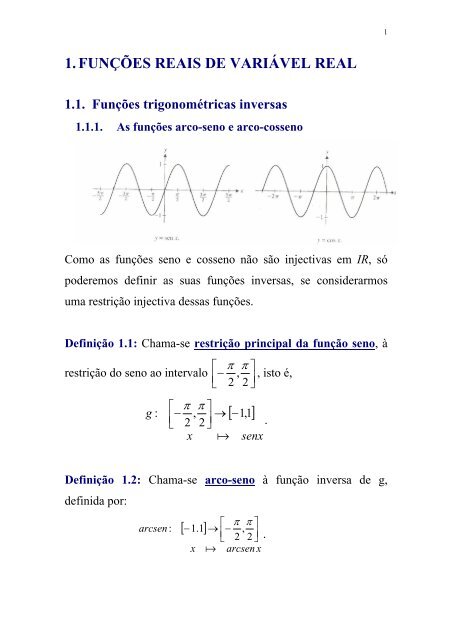
1. FUNÇÕES REAIS DE VARIÁVEL REAL
1.1. Funções trigonométricas inversas
1.1.1. As funções arco-seno e arco-cosseno
Como as funções seno e cosseno não são injectivas em IR, só
poderemos definir as suas funções inversas, se considerarmos
uma restrição injectiva dessas funções.
Definição 1.1: Chama-se restrição principal da função seno, à
⎡ π π ⎤
restrição do seno ao intervalo
⎢
− ,
⎣ 2 2 ⎥
, isto é,
⎦
⎡ π π ⎤
g :
⎢
− , → [ −1,
1]
⎣ 2 2 ⎥
⎦ .
x senx
Definição 1.2: Chama-se arco-seno à função inversa de g,
definida por:
arcsen :
[ −1.
1]
x
⎡ π π ⎤
→
⎢
− ,
⎣ 2 2 ⎥
⎦ .
arcsen x
1

Pela definição da função inversa, temos
⎪
⎧ sen y = x
y = arcsen x ⇔ ⎨ π π .
⎪⎩
− ≤ y ≤
2 2
Gráfico da função g Gráfico da função arco-seno
Nota: A função arco-seno é crescente.
Exemplo 1.3: Calcule arcsen
2
.
2
Exemplo 1.4: Caracterize a função inversa de
1
f ( x)
= arcsen(
3x
−1)
.
2
Definição 1.5: Chama-se restrição principal da função cosseno,
à restrição de cosseno ao intervalo [ , π ]
g : [ 0,
π ] → [ −1,
1]
x
0 , isto é,
.
cos x
2

Definição 1.6: Chama-se arco-cosseno à função inversa de g,
definida por:
arccos :
[ −1.
1]
→ [ 0,
π ]
.
x arccos x
Pela definição da função inversa, temos
y = arccos x
⎧cos
y = x
⇔ ⎨ .
⎩0
≤ y ≤ π
Gráfico da função arco-cosseno
Nota: A função arco-cosseno é decrescente.
Exemplo 1.7: Calcule ⎟ ⎛ 2 ⎞
arccos ⎜
⎜−
.
⎝ 2 ⎠
Exemplo 1.8: Caracterize a função inversa de
( x)
= cos( 3x
+ 2)
−1
f .
3

1.1.2. A função arco-tangente
Como a função tangente não é injectiva no seu domínio, só
poderemos definir a sua função inversa, se considerarmos uma
restrição injectiva dessa funçõe.
Definição 1.9: Chama-se restrição principal da função
⎤ π π ⎡
tangente, à restrição da tangente ao intervalo
⎥
− ,
⎦ 2 2 ⎢
, isto é,
⎣
g :
⎤ π π ⎡
⎥
− ,
⎢
→ IR
⎦ 2 2 ⎣
x tg x
Definição 1.10: Chama-se arco-tangente à função inversa de g,
definida por:
arctg :
⎤ π π ⎡
IR →
⎥
− ,
⎦ 2 2 ⎢
⎣ .
x arctg x
⎪
⎧ tg y = x
Por definição, temos y = arctg x ⇔ ⎨ π π .
⎪⎩
− < y <
2 2
4

Gráfico da função arco-tangente
Nota: A função arco-tangente é crescente.
Exemplo 1.11: Calcule ( − 3)
arctg .
Exemplo 1.12: Caracterize a função inversa de ( x)
= tg(
x − π )
1.2. Limites e continuidade
Definição 2.1: Seja IR
lim f ( x)
= f ( x)
x→a
−
lim e for finito.
x→a
+
a ∈ . Diz-se que f ( x)
x→a
f .
lim existe se e só se
Definição 2.2: Uma função f diz-se contínua num ponto a se as
seguintes condições são satisfeitas:
i) f ( a)
está definida;
ii) f ( x)
lim existe;
x→a
iii) lim f ( x)
= ( a)
x→a
f .
5

Propriedades 2.3:
1. Se f e g são funções contínuas, então também são contínuas
as funções:
f
f + g , f − g , f ⋅ g , com g ≠ 0 ,
g
n
f , n f , com n ∈ IN .
2. A restrição de uma função contínua é ainda uma função
contínua.
Exercício 2.4: Estude a continuidade no ponto x = 0 da função
⎧ 2 −1
⎪
< 0
( ) = ⎨ln(
1−
)
⎪
⎩ cos ≥ 0
2
x
se x
f x x
.
x se x
1.3. Derivada de ordem n
1.3.1. Definição de derivada.
Definição 3.1: Seja f D x0 ∈ . Chama-se derivada de f no ponto
x , ao número real ( x )
0
( x )
f ′ =
0
f ′ definido por
lim
x→x0
0
f
( x)
− f ( x )
x − x
0
Definição 3.2: A equação da recta tangente ao gráfico da
função f é dada por
( x ) = f ′ ( x )( x x )
y − f
− .
0
0
0
0
.
6

Definição 3.3: A equação da recta normal ao gráfico da função
f é dada por
1
y − f ( x0
) = − − .
f ′
( x x0
)
( x )
Nota: Efectuando a mudança de variável 0 x x h −
definição equivalente:
( x )
f ′ =
0
lim
h→0
0
( x + h)
− f ( x )
f 0
0
Exercício 3.4: Considere a função ( x)
h
.
7
= , obtém-se a
1
f = . 2
x − 3
1) Calcule, utilizando a definição, a derivada da função f no
ponto ( , 1)
2 .
2) Determine a equação da recta tangente ao gráfico de f no
ponto ( , 1)
2 .
Definição 3.5: Diz-se que a função f é diferenciável no ponto x 0
se tem derivada finita nesse ponto.
Nota: ( x )
− ( ) x
′ 0
f =
−
f ′ existe se e só se ( ) x
+
f = ( ) x
x
0
lim x
−
→ 0
f
( x)
− f ( x )
x − x
0
0
′ 0
+
e ( ) x
′ 0
f =
x
lim x
+
→ 0
′ 0
f ∈ IR , sendo
f
( x)
− f ( x )
x − x
0
0
.

Exercício 3.6: Seja f a função definida por
f
⎪⎧
e
( x)
= ⎨
⎪⎩
x
+ 2
3 − x
2
se
se
x ≤ 0
x > 0
. Determine, caso exista, f ′ ( 0)
.
Definição 3.7: Chama-se função derivada a função f ′dada por
′ ′
f : D f → IR
x f ′
( x)
onde f tem derivada finita.
, onde f D ′ representa o conjunto dos pontos
Teorema 3.8: Toda a função diferenciável é contínua.
Se f ′ é uma função diferenciável, podemos definir a sua
derivada. Chama-se derivada de ordem 2 de f, à derivada da
função f ′.
Notação: f ′ .
Definição 3.9: Seja f uma função n vezes diferenciável. Chama-se
derivada de ordem n de f, à derivada da função
representa derivada de ordem n-1 de f.
1.3.2. Regras de derivação.
Exemplo 3.10: Calcule a derivada das seguintes funções:
x 2
2
1) f ( x)
= e ln x
2) f ( x)
= x cos( 3x)
2
3) f ( x)
= cos x
4)
2
( 1−
tgx)
f ( x)
=
3
( ) 1 − n
8
f que

x
⎛ x ⎞ 2
5) f ( x)
= e arcsen(
2x)
6) f ( x)
= arctg⎜
⎟ + x ln x
⎝ x + 1⎠
7)
1
f ( x)
= 8) f ( x)
= arccos(
x)
arctgx
Exemplo 3.11: Determine, usando as regras de derivação, a
função derivada de ( x)
= ⎨
⎪⎩
⎪
⎧3x
−1
se x ≤1
2
se x > 1
x
f .
1.3.3. Derivada da função composta.
Definição 3.12: Sejam f e g duas funções. Chama-se função
composta de g com f à função g f caracterizada por
i) g f
{ }
D = x ∈ IR : x ∈ D ∧ f ( x)
∈ D ;
ii) ( g f )( x)
= g[
f ( x)
]
, ∀ x ∈ Dg
f .
Teorema da derivada da função composta:
Se f é diferenciável no ponto 0
então g f é diferenciável em x 0 e,
f
( g f ) ( x ) = g′
( f ( x ) ) ⋅ f ′ ( x )
0
g
x e g é diferenciável em ( x )
′
.
0
0
0
9
f ,
3
Exercício 3.13: Considere as funções f ( x)
= senx e ( x)
2x
Calcule a derivada da função f g .
g = .

1.3.4. Indeterminações: regra de Cauchy.
O conceito de derivada é também usado para levantar algumas
indeterminações.
0 ∞
1.3.4.1. Levantamento de indeterminações do tipo e .
0 ∞
Regra de Cauchy ou regra de L’Hôpital: Sejam c um ponto do
intervalo ( a, b)
e f, g duas funções diferenciáveis em ( b)
excepto possivelmente em c.
Se
Então
′ ;
(i) g ( x)
≠ 0 ∀x
∈(
a,
b)
| { c}
(ii)
desde que
lim
x→c
lim
x→c
f
g
lim
x→c
f ′
g′
( x)
( x)
f
g
( x)
( x)
( x)
( x)
Exemplo 3.14: Calcule
0 ∞
é uma indeterminação do tipo ou .
0 ∞
= lim
x→c
f ′
g′
( x)
( x)
seja definido ( ∈ IR ).
x − x
e − e
lim
x→0 sen x
1.3.4.2. Indeterminações do tipo ∞ − ∞ e 0 ⋅ ∞ .
• Se
lim ( ) 0
x→c
f x = e
lim ( x)
= ∞
x→c
,
g , então
.
x→c
10
a, ,
lim ( x)
⋅ g(
x)
= 0.
∞
f .

Esta indeterminação pode ser transformada numa indeterminação
0 ∞
do tipo ou , escrevendo
0 ∞
( )
( )
f x
f ( x)
⋅ g(
x)
=
1 g x
Exemplo 3.15: Determine lim+
Exemplo 3.16: Determine
g x
f ⋅ =
1 f x
ou ( x)
g(
x)
x→0
2
x ln(
x)
.
⎛ 1 ⎞
xtg⎜
.
⎝ x
x→+∞ lim ⎟
⎠
( )
( )
• Para as indeterminações do tipo ∞ − ∞ , escreve-se a
diferença como uma única fracção.
Exemplo 3.17: Determine
x 3 − x
− .
x x −1
x 1
lim
→1
1.4 Derivadas de funções definidas implicitamente.
Consideremos a relação y = x cos x.
Esta relação define y
explicitamente como uma função de x. De facto, podemos
escrever f ( x)
x cos x
teste da recta vertical.
4
4
2 −
= sendo f uma função, ou seja, f satisfaz o
Até agora, as funções que consideramos eram todas definidas
desta maneira. No entanto, uma função também pode ser definida
implicitamente por uma equação que poderá ser ou não resolvida
em relação a x.
.
11

Além disso, como veremos a seguir, uma equação com duas
variáveis x e y pode definir implicitamente diferentes funções de
x.
2 =
Consideremos a equação x − y 0.
Esta equação não pode ser
revolvida de modo a que y seja definida como uma função
explícita de x. De facto, y = ± x não representa uma função de x.
Neste caso, diz-se que f ( x)
= x e g( x)
− x
12
= são definidas
implicitamente como funções de x pela equação original.
O gráfico das funções f e g representam o ramo superior e inferior
da parábola representada na figura abaixo. A parábola no seu
todo, correspondente ao gráfico da equação x − y 0,
ou seja
2
x = y que não é o gráfico de uma função.
Exercício 4.1: Quantas funções implícitas diferentes são definidas
pela equação x + y = 1.
2
2
2 =

Equações como sen( x 2 y)
= 2x
cos y
+ ou y + 2y
= x − 2x
− 3
podem ser difíceis ou até impossíveis de resolver.
Apesar disso, é sempre possível calcular a derivada de uma
função definida implicitamente, usando um processo chamado
diferenciação implícita que consiste em derivar ambos os
membros da equação dada em ordem a x.
dy
Notação: y′ ( x)
e representam a derivada de y em ordem a x.
dx
Exemplo 4.2: Considere a equação x + y = 1.
Use o processo
de diferenciação implícita para calcular a derivada y′ ( x)
.
Resolução: Derivando ambos os membros da equação em ordem
a x, vem
d
dx
2 2 ( x + y ) = 0
dy dy x
⇔ 2 x + 2y
= 0 ⇔ = − .
dx dx y
dy
Nota: Em geral, a expressão de depende da variável x mas
dx
também de y.
2
2
4
3
13

Exemplo 4.3: Determine a equação da recta tangente a curva
2 2
definida por x + y = 1,
no ponto ⎟ ⎛ 1 3 ⎞
⎜ , .
⎝ 2 2 ⎠
Exercício 4.4: Determine a equação da recta tangente a curva
definida por sen( x 2 y)
= 2x
cos y
⎛ ⎞
+ , no ponto ⎜0,
⎟
⎝ 2 ⎠
π .
Exercício 4.5: Determine a derivada de ordem 2 da função
definida implicitamente por y + 2y
= x − 2x
− 3.
( n)
d y
Notação: y e n
dx
ordem a x.
n
4
3
representam a derivada de ordem n de y em
14