72 Uma piscina tem as seguintes dimensões: 5 m de largura, 7 m de ...

p. 31
70 Quantos litros de água cabem em um cubo de aresta 8 dm?
Resolução:
V 5 a 3
V 5 8 3 5 512 dm 3 → V 5 512 ,
71 Determine o volume de um cubo cuja diagonal é D 5 2 3 m.
Resolução:
D 5 2 3 m
D 5 a 3 5 2 3 → a 5 2 m
V 5 a 3 5 2 3 → V 5 8 m 3
512 ,
72 Uma piscina tem as seguintes dimensões: 5 m de largura, 7 m de comprimento e 2 m de
profundidade. Qual é a capacidade máxima de água dessa piscina em litros? 70 000 ,
Resolução:
V 5 a ? b ? c 5 5 ? 7 ? 2 5 70 m 3 5 70 000 dm 3 5 70 000 ,
73 Num paralelepípedo retângulo, cada uma das bases é um retângulo em que um lado é o triplo do
outro. A altura do prisma é 10 cm e sua área total é 294 cm2 . Determine o volume. 270 cm3 Resolução:
S t 5 2 ? (a ? 3a 1 a ? 10 1 3a ? 10) 5 294
2 ? (3a 2 1 40a) 5 294
2 240 1 600 1 1 764
3a 1 40a 2 147 5 0 → a 5
6
a 5 3 cm; 3a 5 9 cm
V 5 3 ? 9 ? 10 5 270 cm 3
a
3a
10
8 m 3
a
5 3
ou
49
3 ( a 5 2 não convém)

74 (Unesp-SP) Quantos cubos A precisa-se empilhar para formar o paralelepípedo B?
A
a) 60 c) 94 e) 48
b) 47 d) 39
Resolução:
Para formar o paralelepípedo B, são necessários 5 ? 3 ? 4 5 60 cubos A.
B
75 (Faap-SP) Uma piscina retangular de 10,0 m 3 15,0 m e de fundo horizontal está com água até a altura
de 1,5 m. Um produto químico em pó deve ser misturado à água, à razão de um pacote para cada 4 500 ,. O
número de pacotes a serem usados é:
a) 45 c) 55 e) 75
b) 50 d) 60
Resolução:
V 5 a ? b ? c 5 10 ? 15 ? 1,5 5 225 m3 5 225 000 dm3 5 225 000 ,
n 5
225 000
4 500
5 50 pacotes
76 (Unesp-SP) A água de um reservatório na forma de um paralelepípedo retângulo de comprimento
30 m e largura 20 m atingia a altura de 10 m. Com a falta de chuvas e o calor, 1 800 m3 da água do
reservatório evaporaram. A água restante no reservatório atingiu a altura de:
a) 2 m c) 7 m e) 9 m
b) 3 m
Resolução:
V 5 10 ? 30 ? 20 5 6 000 m
d) 8 m
3
água restante 5 V 2 1 800 5 6 000 2 1 800 5 4 200 m3 4 200 5 30 ? 20 ? h → h 5 7 m
A água restante atingiu a altura de 7 m.
77 (UFPR) Ao se colocarem 192 , de água em um reservatório cujo interior tem a forma de um cubo
com uma das faces na horizontal, o nível da água sobe 30 cm. Qual é a capacidade desse reservatório?
a) 640 c) 576 e) 512
b) 768 d) 384
Resolução:
30 cm 5 3 dm
192 , 5 192 dm3 → volume de água em 3 dm
V 5 192 5 a ? a ? 3 → a2 5 64 → a 5 8 dm
V 5 a3 5 83 5 512 dm3 5 512 ,
A capacidade do reservatório é 512 ,.

78 (Unesp-SP) Considere um pedaço de cartolina retangular de lado menor 10 cm e lado maior 20 cm.
Retirando-se 4 quadrados iguais de lados x cm (um quadrado de cada canto) e dobrando-se na linha pontilhada
conforme mostra a figura, obtém-se uma pequena caixa retangular sem tampa.
O polinômio, na variável x, que representa o volume, em cm 3 , dessa caixa é:
a) 4x 3 2 60x 2 1 200x c) 4x 3 2 60x 2 1 200 e) x 3 2 15x 2 1 50x
b) 4x 3 2 60x 1 200 d) 4x 3 2 30x 2 1 200x
p. 32
x cm
Resolução:
Montando a caixa, temos:
10 2x
20 2x
20 cm
V 5 x ? (10 2 2x) ? (20 2 2x) 5 4x 3 2 60x 2 1 200x
79 (Unesp-SP) Considere o sólido resultante de um paralelepípedo retângulo de arestas medindo x, x
e 2x, do qual um prisma de base quadrada de lado 1 e altura x foi retirado. O sólido está representado pela
parte escura da figura.
x
x
O volume desse sólido, em função de x, é dado pela expressão:
a) 2x 3 2 x 2 c) 2x 3 2 x e) 2x 3 2 2x
b) 4x 3 2 x 2 d) 2x 3 2 2x 2
Resolução:
V 5 x ? x ? 2x 2 1 ? 1 ? x 5 2x 3 2 x
x
2x
1
10 cm

80 (Cesgranrio-RJ) De um bloco cúbico de isopor de aresta 3a recorta-se o sólido, em forma de H,
mostrado na figura. O volume do sólido é:
a) 27a 3 c) 18a 3 e) 9a 3
b) 21a 3 d) 14a 3
p. 34
a
a
a
a a a
Resolução:
V 5 (3a) 3 2 2 ? a ? a ? 3a 5 27a 3 2 6a 3 → V 5 21a 3
81 Uma barra de chocolate tem o formato de um prisma triangular regular de aresta lateral 15 cm e
aresta da base 3 cm. Qual o volume de chocolate contido na barra? (Considere 3 5 1,7. ) 57,375 cm3 Resolução:
3
15
V 5 S ? h
S
V
b
b
5
1
3 ? 3
3
5
2 2
9 3
5 ? 15 5
4
9 3
4
135 3
4
82 (Fuvest-SP) Dois blocos de alumínio em forma de cubo, com arestas medindo 10 cm e 6 cm, são
levados juntos à fusão e em seguida o alumínio líquido é moldado como um paralelepípedo reto de arestas
8 cm, 8 cm e x cm. O valor de x é:
a) 16 c) 18 e) 20
b) 17 d) 19
Resolução:
V 1 5 10 3 5 1 000 cm 3
V 2 5 6 3 5 216 cm 3
V t 5 1 000 1 216 5 1 216 cm 3
V t 5 1 216 5 8 ? 8 ? x → x 5 19 cm
→ V 5 57,375 cm3
3a

83 (UFRJ) Uma barra de sabão ABCDEFGH, com a forma de um paralelepípedo retângulo, foi cortada
pelo plano que contém os pontos C, D, F e G, como mostrado na figura 1. O sólido ABCDFG obtido foi
cortado, mais uma vez, pelo plano que contém os pontos M, N, P e Q, que são, respectivamente, os pontos
médios das arestas AD, BC, CG e DF, como ilustrado na figura 2.
F
A
B
G
D
E
H
C
F
figura 1 figura 2 figura 3
Calcule a razão entre o volume do sólido CDMNPQ resultante desse segundo corte (ilustrado na figura 3) e o
volume da barra de sabão original. 1
8
G
Q
B
A M
84 (UFSC) Na figura a seguir, o segmento de reta AE é paralelo ao segmento BF, e o segmento de reta
CG é paralelo ao segmento DH; o trapézio ABDC tem os lados medindo 2 cm, 10 cm, 5 cm, e 5 cm, assim
como o trapézio EFHG; esses trapézios estão situados em planos paralelos que distam 4 cm um do outro.
G
Resolução:
Sejam AD 5 a, CD 5 b e AF 5 c.
V 5 a ? b ? c
inicial
DM 5
a
; MQ 5
2
c
2
V2
5
1
2
?
a
2
?
c
2
? b 5
abc
8
V
V
E
A
F
C D
G
2
inicial
A razão é 1
8
Resolução:
5
abc
8
abc
5
5
E
.
B
A
F
2
C 10 D
H
1
8
B
Consideremos a figura acima um prisma
quadrangular de altura 4 cm, cujas bases
são trapézios de B 5 10 e b 5 2.
H
5
D
P
N
C
Q
M
Calcule o volume (em cm3 ) do sólido limitado pelas faces ABFE, CDHG,
ACGE, BDHF e pelos dois trapézios. 72 cm3 D
P
N
C
2
2
h2 5 52 2 42 5 9 → h 5 3
(B 1 b)h (10 1 2)
Sbase
5 5
2
2
V 5 S ? H b
V 5 18 ? 4 5 72 cm3 h
5
4
3
5 18

85 A área lateral de um prisma hexagonal regular é 48 cm2 , e a altura do prisma é o dobro da aresta da
base. Determine seu volume. 24 3 cm 3
Resolução:
a
2a
86 Num prisma hexagonal regular, a altura mede 3 m e o apótema da base mede 2 3 m. Determine
seu volume. 72 m3 Resolução:
h
y
H
h
A altura do prisma é o lado do retângulo da face lateral, então:
S , 5 6 ? a ? h 5 48 → a ? h 5 8
h 5 2a → a ? 2a 5 8 → a 2 5 4 → a 5 2 cm
h 5 2 ? 2 → h 5 4 cm
Sb 5 6 ?
1
2
? 2 ?
2 3
2
5 6 3 cm
V 5 S ? h
b
V 5 6 3 ? 4 → V 5 24 3 cm
A base é um hexágono regular de apótema h 5 2 3 m e H 5 3 m.
h 5
, 3
2
5 2 3 → , 5 4 m
V 5 S ? H
4 ? 2 3
Sb 5 6 ? 5 24 3 m
2
V
87 (UFPE) Um depósito na forma de um paralelepípedo retângulo está
preenchido com certo volume de líquido. Ao colocarmos no interior do
paralelepípedo um cubo sólido de aresta 4 cm, com densidade maior que a do
líquido, a altura do líquido fica igual à aresta do cubo. O paralelepípedo tem base
com comprimento 5 cm e largura 6 cm. Determine a aresta x de outro cubo
sólido, com densidade maior que a do líquido, que, quando colocado no interior do
paralelepípedo, deixa a altura do líquido igual à medida da aresta. Indique (x 1 2) 2 .
b
5 24 3 ? 3
3
→ V 5 72 m 3
Resolução:
O volume do líquido é: 30x 2 x3 5 30 ? 4 2 43 x3 2 43 2 30x 1 30 ? 4 5 0
Fatorando a expressão, temos:
(x 2 4) ? (x2 1 4x 116) 2 30 ? (x 2 4) 5 0
(x 2 4) ? (x2 1 4x 2 14) 5 0 → x 5 4 ou x 5 22 1 3 2
Então: (x 2) 2
1 5 22 1 3 2 1 2 5 18
x 5 18
( )
2
2
2
18

88 (Unicamp-SP) Uma caixa-d’água cúbica, de volume máximo, deve ser colocada entre o telhado e a
laje de uma casa, conforme mostra a figura. Dados: AB 5 6 m, AC 5 1,5 m e CD 5 4 m.
C
A
D
Resolução:
a) Seja x a altura da caixa-d’água.
B
a) Qual deve ser o comprimento de uma aresta da caixa? 1,2 m
b) Supondo que a altura máxima da água na caixa é de 85% da altura da
caixa, quantos litros de água podem ser armazenados na caixa? 1 468,8 ,
89 Determine o volume de um prisma triangular regular cuja aresta da base é 5 cm sabendo que a área
de cada face lateral é o dobro da área de uma das bases. 375
8 cm3
Resolução:
5
1,5
1,5 x
H
C
F
A
x
x
E
Os triângulos CFE e CAB são semelhantes, então:
1,5 2 x
x
1,5
5
6
→ 9 2 6x 5 1,5x → x 5 1,2 m
O comprimento de uma aresta deve ser 1,2 m.
b) h 5 85% de 12 5
85
100
? 12 5 10,20 dm
V 5 12 ? 12 ? 10,20 5 1 468,8 dm3 → V 5 1 468,8 ,
Sb 5
2
5 3
4
2
cm
S, 5 2 ? Sb 5
25 3
2
2
cm
S, 5 5 ? H 5
25 3
2
→ H 5
5 3
2
cm
V S H V
375
8 cm
5 b ? 5
2
5 3
4
?
5 3
2
→
5
6
3
B

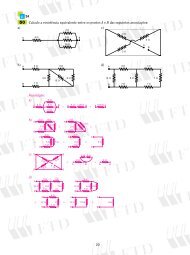
90 Calcule o volume de um prisma quadrangular regular cuja área total tem 256 m2 e a área lateral é
igual ao dobro da área da base. 256 m3 Resolução:
a
91 (UFV-MG) A figura abaixo exibe a seção transversal de uma piscina de 20 m de comprimento por
10 m de largura, com profundidade variando uniformemente de 1 m a 3 m.
1 m
20 m
a) Determine o volume de água necessário para encher a piscina até a borda. (Sugestão: Calcule a área da
seção transversal da piscina ilustrada pela figura.) 400 m
b) Qual a distância mínima que uma pessoa de 1,70 m deve caminhar, saindo do ponto mais raso da piscina,
para que fique totalmente submersa? (Sugestão: Use semelhança de triângulos.)
3
7 m
Resolução:
a)
b)
1 m
1 1
A
a
h
x C
D
0,70
S t 5 256 5 2 ? (a ? a 1 a ? h 1 a ? h) → 256 5 2 ? (a 2 1 2ah) → a 2 1 2ah 5 128
S, h
5 5 5
4ah 2a 2 →
Substituindo h na primeira equação, temos:
2
a 1 2a ?
a
2
2
5 2a 5 128 → a 5 8 m
h 5
8
2
→ h 5 4 m
20 m
20 x
1
B
2
E
3 m
0
a
2
V 5 S b ? h 5 a 2 ? h 5 64 ? 4 → V 5 256 m 3
10 m
3 m
Considerando a piscina um prisma
de altura 10 m, cujas bases são os
trapézios, temos:
V 5 S ? h
b
V 5
V
1 ( 1 3) 20
? 10 → 5 400 m
2
3
O triângulo ABE é semelhante ao triângulo ACD, então:
x
0,70
5
20
→ x 5 7 m
2
A distância mínima é 7 m.

p. 38
92 Determine a natureza de uma pirâmide que possui:
a) 8 faces heptagonal
b) 12 arestas
93 Determine o número de diagonais da base de uma pirâmide sabendo que a soma dos ângulos de
todas as faces é igual a 1 8008. 9
Resolução:
Seja S a soma dos ângulos internos da base.
i
S 5 (n 2 2) ? 180°
i
As faces laterais são triângulos, então:
S 5 1 800° 5 (n 2 2) ? 180° 1 180°n
360°n 5 2 160°
n 5 6
A base é um hexágono.
n ? 2
D 5 5 D
?
(n 3) 6 3
→ 5 9
2
2
94 Qual a área lateral de uma pirâmide quadrangular regular de altura 5 m e área da base igual a
100 m2 ? 100 2 m 2
Resolução:
5
O
V
5
a A
g
M
a
B
hexagonal
Resolução:
a) A pirâmide possui 8 faces; então, uma das faces é a base, portanto é uma pirâmide heptagonal.
b) A pirâmide possui 12 arestas; 12
2
Portanto, a pirâmide é hexagonal.
5 6 → número da aresta da base
a2 5 100 → a 5 10 m
Aplicando o teorema de Pitágoras no triângulo VOM, temos:
2
g
2 2
5 5 1 5 → g 5 5 2 m
S,
5 4 ?
a ? g
2
5 4 ?
10 ? 5 2
2
2
5 100 2 m

95 Qual a altura de um tetraedro regular de 6 m de aresta? 2 6 m
Resolução:
C
a
M
D
a a
g h
a
H
A
a 6 6 6
h 5 5 → h 5 2 6 m
3 3
a
B
96 Determine a área lateral e a área total de uma pirâmide quadrangular regular cujas arestas da base
medem 6 cm e a altura, 4 cm.
Resolução:
4
O
V
3
6 A
g
M
6
B
S , 5 60 cm 2 e S t 5 96 cm 2
97 Determine as áreas lateral e total de uma pirâmide triangular regular, sendo 7 m a medida do seu
2
2
apótema e 24 m o perímetro da base. S, 84 m e St 4 21 m
5 5 1 4 3 ( )
Resolução:
p 5 24 → a 5
24
5 8
3
V
B C
8
A
7
8
Aplicando o teorema de Pitágoras no triângulo VOM, temos:
g2 5 42 1 32 → g 5 5 cm
S 60 cm 2
, 5 ?
6 ? 5
4 5
2
S 5 6 b 2 5 36 cm2 S T 5 S , 1 S b
S T 5 60 1 36 5 96 cm 2
S,
5 3 ?
7 ? 8
2
5 84 m
S 5 S 1
2
S
T
,
b
Sb
5
2
8 3
4
5 16 3
S 5 84 1 16 3 5 4 ? 21 1 4 3 m
T
( )
2

98 Calcule a área da base de uma pirâmide quadrangular regular, cujas faces laterais são triângulos
eqüiláteros, sendo 49 3 cm 2 a soma das áreas desses triângulos. 49 cm2 Resolução:
a
99 Considere a pirâmide com um triedro trirretangular cujas arestas laterais medem 10 cm. Determine
sua área total. S 5 50 3 1 3
2
cm
Resolução:
t
g
a
a
( )
10
100 A altura de um tetraedro regular é 4 6 m. Determine o apótema do tetraedro e a área da base.
C
a
M
D
a a
g h
a
H
A
a
a
S,
a a
5 ? 5 5 5
4
2
3
2
49 3 → 3 49 3 → 7 cm
4
S b 5 a 2 5 7 2 5 49 cm 2
2 2 2
a 5 10 1 10 5 200 → a 5 10 2 cm
S 5 S 1 S
S
T , b
,
10 ? 10
5 3 ? 5 150 cm
2
Sb
5
2
a 3
4
5
200 3
4
5 50 3 cm
S 5 150 1 50 3 5 50 ? 3 1 3
T
Resolução:
2
( ) cm 2
B
2
10
a
10
a 6
h 5 5 4 6 → a 5 12 m
3
g
S b
a 3
5 5 12 g 5 m
2
3
→ 6 3
2
2 2
a 3 12 3
5 5 5 36 3
m
4 4
g 5 6 3 m e S 5 36 3 m
2
b
2

101 Determine a área lateral e a área total de uma pirâmide hexagonal regular sabendo que a aresta da
base mede 6 3 cm e a sua altura, 12 cm.
2
2
S, cm e St 432 cm
5 5
270 3 3
Resolução:
p. 40
12
6 3
h
g
102 A altura de uma pirâmide quadrangular regular é 10 m, e sua base tem lado 8 m. Determine seu
volume. 640 3
m
3
Resolução:
P
A 10 B
C D
8
103 Determine o volume de uma pirâmide de altura 7 cm, cujo polígono da base é um triângulo isósceles
de lados 13 cm, 13 cm e 10 cm. 140 cm3 Resolução:
Sb ? h
V 5
3
13 13
h
5 5
h é o apótema da base da pirâmide.
a 3 6 3 ? 3
h 5 5
→ h 5 9
2 2
g é o apótema da pirâmide.
g2 5 92 1 122 → g2 5 81 1 144 → g2 5 225 → g 5 15 cm
S,
5 6 ?
a ? g
2
5 6 ?
6 3 ? 15
2
2
5 270 3 cm
S 5 S 1 S
T , b
b 5 6 ?
( 6 3 ) 2
Sb ? h 8 ? 8
V 5 5 ? 10 5
3 3
S
4
3
2
5 162 3 cm
S 5 270 3 1 162 3 5 432 3 cm
T
h 2 5 13 2 2 5 2 5 169 2 25 5 144 → h 5 12 cm
S
V
b
640
3 m3
5
1
2
? 10 ? 12 5 60 cm
5
60 ? 7
3
3
5 140 cm
2
2

104 O apótema da base de um tetraedro regular mede 3 cm. Determine seu volume.
Resolução:
C
a
a
105 (ITA-SP) A razão entre a área da base de uma pirâmide regular de base quadrada e a área de uma das
faces é 2. Sabendo que o volume da pirâmide é de 12 m 3 , temos que a altura da pirâmide mede (em metros):
a) 1 c) 3 e) 5
b) 2 d) 4
Resolução:
2
a
1
a ? g
2
a
H
O
V
H
V
A
3
g
a
2
a
g
M
O M
5 2 → 2a 5 2g → a 5 g
B
a
hb
a b 5 3 5 → hb 5 9 cm 5 g
3
a 3
h 5 → a 5 18
3
→ a 5 6 3 cm
2
3
Sb
5
2
a 3
4
5
36 ? 3
4
3
2
5 27 3 cm
H 5
a 6
3
5
6 3 ?
3
6
5 2 18 5 6 2 cm
V 5
1
Sb 3
? H 5
1
3
? 27 3 ? 6 2 5 54 6 cm
Aplicando o teorema de Pitágoras no triângulo VOM, temos:
( )
2 2
g 5 H 1 a
2
Como a 5 g, temos:
2
2
a 2
2
a
4
2
5 H
2
→ H 5
3a
4
2
→ a 5
V 5 12 5
1 2
a H
3
Substituindo a 2 , temos:
4H
3
2 2
2
12
1
3
5 ?
4H
? H → H 5 27 →
H 5 3
3 3
54 6 cm 3
3

106 (UFBA) Em uma pirâmide de altura h metros, a área da sua base é 560 m2 . Um plano a, paralelo à
base a uma distância de h
metros do vértice da pirâmide, determina uma secção transversal de área:
2
a) 280 m2 c) 140 m2 e) 80 m2 b) 180 m2 d) 100 m2 Resolução:
107 (Unicamp-SP) Considere um cubo cuja aresta mede 10 cm. O sólido cujos vértices são os centros das
faces do cubo é um octaedro regular, cujas faces são triângulos eqüiláteros congruentes.
a) Calcule o comprimento da aresta desse octaedro regular.
b) Calcule o volume do mesmo octaedro.
500
3 cm3
Resolução:
a) De acordo com o enunciado, temos a figura:
5 2 cm
B
10 A
E
C
10
F
D
2
⎛ ⎞
2
SB
5
H 560
5
h 560
S ( 1 h ) → ⎜ ⎟ → 5 4 → S 5
560
1 5 140 m
S ⎜ 1 h ⎟ S1
4
⎝ 2 ⎠
5
M
5
No triângulo CDM, temos:
(CD) 2 5 52 1 52 5 50 → CD 5 5 2 cm
b) O octaedro é composto por duas pirâmides, então:
V 5 ? a ? 5 ? ? ? 5 cm
2
1
5 2
1
25 2 5
500
3
3 3
2 3
5
5
2

p. 41
108 Na figura, os quadrados ABCD e A9B9C9D9, cujos lados medem
10 u.c., são as bases de um prisma reto de altura igual a 5 3 u.c., e o ponto O
O
é, ao mesmo tempo, o centro do quadrado ABCD e o vértice da pirâmide com
base A9B9C9D9.
A partir dessas informações, pode-se afirmar:
(01) Qualquer plano que contenha uma face lateral da pirâmide faz um
A
D
B
ângulo de 60º com o plano da base A9B9C9D9.
A B
(02) Qualquer aresta lateral da pirâmide faz um ângulo de 60º com o plano da base A9B9C9D9.
(04) Existem uma aresta da pirâmide que é coplanar ao segmento DD9 e uma aresta da pirâmide que está
contida numa reta reversa à reta que contém DD9.
(08) A área do triângulo OC9D9 é igual a 50 u.a.
(16) O volume do sólido compreendido entre o prisma e a pirâmide é igual a
Resolução:
De acordo com o enunciado, temos:
A
A
10
D 10
D
g
5
10
O
5 3
B
B
10
C
5 3
C
500 3
3
2 2
(01) (Verdadeira); g 5 5
2
1 ( 5 3 ) 5 100 → g 5 10
sen a 5
5 3
10
5
3
2
→ a 5 60°
(02) (Falsa); seja a a aresta lateral. No triângulo OCC9, OC 5 5 2 → (OC9) 2 5 a2 1 (CC9) 2
a2 5 50 1 75 5 125 → a 5 5 5
O ângulo b formado pela aresta e pelo plano A9B9C9D9:
sen b 5
5 3
5 5
→ b 60°
(04) (Verdadeira); B9O e A9O são reversas com D9C9.
(08) (Verdadeira); g 5 10 e aresta da base 5 10, portanto: S 5
(16) (Falsa); V 5 V 2 V prisma pirâmide
1
10 ? 10 5 50 u.a.
2
Vprisma 5 10 ? 10 ? 5 3 5 100 3
Vpirâmide 5
1
10 ? 10 ? 5
3
3
100
3
5
3
V 5 100 3
100 3
2
3
5
200 3
3
soma 5 1 1 4 1 8 5 13
u.v.
D C
13
C

109 Calcule o volume de uma pirâmide triangular regular sabendo que o apótema da base mede 8 cm e o
apótema da pirâmide, 10 cm.
Resolução:
384
3
3 cm
110 (UFRJ) Observe as figuras a seguir.
3 m
F
C
C
F 6 m
E
C
C
M
a
A
10
F
8
H
D
H
6 m
A 4 m B
1,7
1,5
M
6 m
A
4 m
figura 1
figura 2
Resolução:
a) De acordo com a figura, temos:
h
B
B
h
D
a
B
D
B
D
E
O apótema da base é 8, então: h 5 24.
h 5
a 3
2
→ 24 5
a 3
2
→ 48 5 a 3 → a 5
48 3
3
5 16 3 cm
2
H
2
5 10 2 8 5 36
2
→ H 5 6 cm
V 5 Sb ? H
Sb
5
a
5 5 cm
V 5 ?
2
1
3
2
3
4
2 563 3
4
192 3
1
3
192 3
3
? 6 5 384 3 cm
E
D
E
h
3 m
3,4 m
A figura 1 mostra a forma do toldo de uma barraca, e a
figura 2, sua respectiva planificação, composta de dois
trapézios isósceles congruentes e dois triângulos.
Calcule:
a) a distância h da aresta AB ao plano CDEF 0,8 m
b) o volume do sólido de vértices A, B, C, D, E e F,
mostrado na figura 1, em função de h 8h
h 2 5 1,7 2 2 1,5 2 5 2,89 2 2,25 5 0,64 → h 5 0,8 m
b) O volume do sólido é o volume do prisma mais 2 ? volume da pirâmide.
MD 5 1
A B
Vprisma 5 Sb ? H 5
3h
2
? 4 5 6h
E
Vpirâmide 5
1
3
? Sb
? h 5
1
3
? 1 ? 3 ? h 5 h
C N
M D
V 5 6h 1 2h 5 8h

111 (ITA-SP) Considere uma pirâmide regular de altura igual a 5 cm e cuja base é formada por
um quadrado de área igual a 8 cm 2 . A distância de cada face dessa pirâmide ao centro de sua base, em
centímetro, é igual a:
a)
b)
15
3
5 6
9
Resolução:
2
S 5 8 5 , → , 5 2 2 cm
E
b
D
2 2
5
A
P
c) 4 3
5
d) 7
5
112 (Fuvest-SP) A base ABCD da pirâmide ABCDE é um retângulo de
lados AB 5 4 e BC 5 3.
As áreas dos triângulos ABE e CDE são, respectivamente, 4 10 e 2 37.
Calcule o volume da pirâmide.
Resolução:
24
D
E
P
A F 4 B
G
Cálculo de PE:
FG 5 3
SABE 5
1
? 4 ? EF 5 4 10 → EF 5 2 10
2
SCDE 5
1
? 4 ? EG 5 2 37 → EG 5 37
2
Nos triângulos EFP e EPG, temos:
(EF) 2 5 (EP) 2 1 (PF) 2
(EG) 2 5 (EP) 2 1 (PG) 2
PG 5 3 2 FP
Então, isolando EP das duas equações, temos:
40 2 (PF) 2 5 37 2 (3 2 PF) 2
40 2 PF2 5 37 2 9 1 6PF 2 PF2 → 12 5 6PF → PF 5 2
(EG) 2 1 (EP) 2 1 (PG) 2 → 37 2
V 5
1
? 4 ? 3 ? 6
5 24
3
3
C
B
2
2
M
2
C
e) 3
A altura de cada face ao centro de sua base é a
altura da pirâmide cuja base é uma das faces
laterais, e o vértice é esse centro v 5 V
1 ( 4
).
v 5
1
?
1
2
? 2 2 ? 5 5
10 3
( ) cm
4 3
3
2 2
(AM) 5 5 1 (
2
2 ) 5 27 → AM 5 3 3 cm
1 2 2
v 5 ?
3
? 3 3
2
? h 5
10
3
5 6
→ h 5
9
cm
E
D
A B
( ) 5 (EP) 2 1 (3 2 FP) 2 → 37 5 (EP) 2 1 1 → EP 5 6
C

113 (ITA-SP) Uma pirâmide regular tem por base um hexágono cuja diagonal menor mede 3 3 cm.
As faces laterais dessa pirâmide formam diedros de 60º com o plano da base. A área total da pirâmide, em
centímetro quadrado, é:
a) 81 3
2
81
c)
2
e) 27 2
b) 81 2
2
Resolução:
d) 27 3
Pelo enunciado, temos a figura:
E
D
0
V
B
120°
O 60°
M
F
A
2
Para determinarmos a área total, necessitamos do , e do apótema VM.
O ângulo E ^
é 120° → pelo teorema dos cossenos, temos:
d2 5 , 2 1 , 2 2 2 ? , ? , ? cos 120°
2
2 2 2
( 3 3 ) 5 , 1 , 2 2,
?
1 ( 2
2 ) → , 5 3 cm
apótema da base OM 5
, 3
2
5
3 3
2
cm
No triângulo VOM, cos 60° 5
1
2
5
OM
VM
→ VM 5 3 3 cm
ST 5 Sb 1 S,
Sb
5 6 ?
2
3 3
4
5
27 3
2
2
cm
S,
5 6 ?
3 ? 3 3
2
5
54 3
2
2
cm
ST
5
27 3
2
1
54 3
2
5
81 3
2
2
cm
C
2

114 (Fuvest-SP) No cubo de aresta a, X e Y são pontos médios das arestas
AB e GH, respectivamente. Considere a pirâmide de vértice F e cuja base é o
quadrilátero XCYE. Calcule, em função de a:
a) o comprimento do segmento XY α 2
b) a área da base da pirâmide
c) o volume da pirâmide a 3
α
3
2 6
2
Resolução:
a)
b)
c)
E
E
E
H Y G
D
A X B
a
H Y G
D
A X a
2
B
H Y G
D
A X B
a
F
F
F
a
C
C
C
2 2 2 2
XY 5 a 1 a 5 2a → XY 5 a
CE é a diagonal do cubo, logo: CE 5 a 3.
XCYE é um losango, portanto: S 5
Dd
.
2
D 5 a 3;
d 5 XY 5 a 2
2
a 3 ? a 2 a 6
S 5
5
2
2
O plano XCYE divide o prisma em dois sólidos congruentes.
volume da pirâmide 5
Vprisma
2
2 2 ?
1
3
?
a
2
?
a
2
? a 5
3
a
2
2
3
a
6
5
3
a
3
2
E
H Y G
D
A X B
F
C

115 (UFPE) As arestas do sólido convexo ilustrado a seguir são obtidas unindo os pontos médios de cada
uma das arestas de um tetraedro regular aos pontos médios das quatro arestas que são concorrentes a elas.
Se a aresta do tetraedro mede 6 2, qual o volume do sólido?
p. 45
Resolução:
O sólido obtido é um octaedro regular de aresta a
2 . Portanto, ao 5 3 2.
O volume do octaedro é determinado ao se obter o volume da pirâmide de altura
h 5
3 2 ?
2
2
5 3
V 5 2 ?
1
3
? ( 3
2
2 ) ? 3 5 36
116 O volume de uma pirâmide é 216 cm3 . Uma secção transversal feita a 3 cm da base determina outra
pirâmide de volume 27 cm3 . Qual a altura da pirâmide? 6 cm
Resolução:
3 3
V1
H 3 27 H 3
5
⎛ 2 ⎞
5
⎛ 2 ⎞ 3 H 2 3
→ → 5 → H 5 6 cm
V ⎝ H ⎠ 216 ⎝ H ⎠ 6 H
117 Calcule a área total do tronco hexagonal regular cuja base menor tem aresta 2 cm a base maior tem
aresta 4 cm, e o apótema do tronco mede 3 cm. ( 54 1 30 3 ) cm 2
Resolução:
2 cm
4 cm
S 5 S 1 S 1 S
S
T b B ,
,
S b
3 cm
5 6 ?
(2 1 4) ? 3
2
2
5 54 cm
5 6 ?
1
2
? 2 ?
2 3
2
2
5 6 3 cm
S
S
B
T
36
2
5 6 ?
1 4 3
? 4 ? 5 24 3 cm
2 2
5 54 1 6 3 1 24 3 5 ( 54 1 30 3 ) cm
2

118 Um tronco de pirâmide tem como base dois quadrados de lados 4 cm e 9 cm, e a altura do tronco é
6 cm. Determine seu volume. 266 cm3 Resolução:
k 5 6; B 5 81; b 5 16
V 5
k
3
? [ B 1 B ? b 1 b]
V 5
6
3
? 81 1 81 ? 16 1 16
( )
V 5 2 ? 133 5 266 cm 3
119 Um banco de cimento tem a forma de um tronco de pirâmide, com
50 cm de altura. Quantos metros cúbicos de concreto foram necessários
para confeccionar esse banco? 1,02 m3 Resolução:
k 5 0,5 m; B 5 0,50 ? 5 5 2,5 m; b 5 0,40 ? 4 5 1,6 m
V 5
k
? B 1 B ? b 1 b
V
[ ]
5
3
0,5
3
? ( 2,5 1 2,5 ? 1,6 1 1,6)
5
120 (UFRJ) Em um tanque no formato de um cubo de aresta 25 cm, contendo líquido, foi posta uma
pirâmide P 1 , de altura igual a 6 cm, com a base apoiada no fundo do tanque.
Com isso, o nível de líquido passou de 18 cm para 19 cm.
a) Calcule o volume, em centímetro cúbico, da pirâmide P . 625 cm 1
b) A pirâmide P foi retirada do tanque e o nível de líquido voltou ao inicial. Uma pirâmide P , de 30 cm de
1 2
altura, foi então posta no tanque, com a base apoiada no fundo, o que elevou em 2 cm o nível do líquido.
3
Determine o volume da pirâmide P 2 .
16 875
13
Resolução:
a) O volume de água deslocado é o volume
da pirâmide.
V 5 25 ? 25 ? 1 5 625 cm 3
0,5
3
18
cm 3
? 6,1 5 1,02 m 3
20
19
50 cm
4 m
5 m
40 cm
b) O volume do tronco é o volume de água deslocado:
V 5 25 ? 25 ? 2 5 1 250 cm tronco 3
V 5 V 2 v
tronco
V
v
3
5
⎛ 30 ⎞
⎝ 30 2 20 ⎠
→ v 5
V
, então:
27
1 250 5 V 2
V
27
5
26V
27
cm 3 16 875
→ V 5
13

p. 46
121 (UFPR) Uma pirâmide de base quadrada, feita de madeira maciça, tem 675 g e 12 cm de altura.
Pretende-se fazer um corte, paralelo à base, para obter uma pirâmide menor. Quantos gramas terá essa
pirâmide se o corte for feito a 4 cm da base?
a) 200 g c) 250 g e) 350 g
b) 225 g
Resolução:
d) 300 g
Pelo enunciado, temos o esquema:
A
I
E
D F G
Sejam V a pirâmide maior e v a pirâmide menor.
3
v
5
8 v
5
8
V ( 12 ) V 27
8
27
5
m
675
5 200
g
→
→ m
122 (Unesp-SP) Com o fenômeno do efeito estufa e
conseqüente aumento da temperatura média da Terra, há
o desprendimento de icebergs (enormes blocos de gelo)
das calotas polares terrestres. Para calcularmos o volume
aproximado de um iceberg podemos compará-lo com sólidos
geométricos conhecidos. Suponha que o sólido da figura,
formado por dois troncos de pirâmides regulares de base
quadrada simétricos e justapostos pela base maior, represente
aproximadamente um iceberg.
As arestas das bases maior e menor de cada tronco medem, respectivamente, 40 dam e 30 dam e a altura
mede 12 dam. Sabendo que o volume V da parte submersa do iceberg corresponde a aproximadamente S 7
30 dam
12 dam
40 dam
8
do volume total V, determine V . 25 900 dam S 3
Resolução:
Vs V
V B B b b
k B
5
7
8
5 2 ?
k
3
? [ 1 ? 1 ]
2 2 2 2
5 12 dam; 5 40 dam ; b 5 30 dam
V 5 2 ?
12
3
2
? ( 40 1
2 2
40 ? 30
2
1 30
)
V 5 8 ? (1 600 1 1 200 1 900) 5 29 600 dam
Vs 5
7
8
? 29
3
600 5 25 900 dam 3
H
B
4 8 cm
C
4 cm
12 cm

123 (Unb-DF)
Minha casa é engraçada
Desenho espetacular
A parede é inclinada
E o chão retangular
Chão e teto semelhantes
Estão em proporção
Oito vezes a área do teto
É a metade da área do chão
Quatro paredes tem a casa
Uma à outra, tão igual
Quatro paredes muito grandes
100 m2 de área lateral
Com uma pergunta quero terminar
Minha altura você pode calcular?
O teto da casa nunca vou alcançar
Pois minha altura teria de dobrar
Uma pista ainda devo anunciar
Em forma de quadrinha singular
Batatinha quando nasce
Se esparrama pelo chão
Ocupando totalmente
Os 64 m2 de extensão
Com base nas informações do texto, faça o que se pede.
a) Calcule a área, em metro quadrado, do teto da casa. 4 m
b) Calcule a altura, em metro, de um dos quatro quadriláteros que formam as paredes da casa.
c) Calcule a altura, em decímetro, do dono da casa.
2
Resolução:
20 dm
a) 8s
S
2 ; 5 S 5 64 m2 → 16s 5 64 → s 5 4 m2 b) S 5 100 → cada face possui , 100
25 m
4
2
5
a 5 2; b 5 8
25 5
(a 1 b)h
2
→ 25 5
(2 1 8)h
2
→ h 5 5 m
c) h2 5 k2 1 32 → 25 5 k2 s
k
a
h
S
b
1 9 → k 5 4 m
Se H é a altura do dono da casa, então: H 5 2 m 5 20 dm.
p. 49
124 Calcule o volume de um cilindro circular de altura 20 cm e raio da base 4 cm.
Resolução:
V 5 S ? H B
V 5 p42 ? 20 5 320p cm3 320p cm 3
5 m

125 A área lateral de um cilindro circular reto é igual à metade da área total. Calcule a altura desse
cilindro sabendo que o raio da base mede 7 cm. 7 cm
Resolução:
S , 5 2pr ? h; S B 5 2pr 2
S T 5 2pr 2 1 2pr ? h
De acordo com o enunciado, temos:
2
2pr 1 2pr ? h 49 1 7h
2pr ? h 5
→ 7h 5 → h 5 7 cm
2
2
126 Determine a área total de um cilindro sabendo que a área lateral é 40p cm2 e sua secção meridiana é
um quadrado. 60p cm2 Resolução:
Se a secção meridiana do cilindro é um quadrado, então: h 5 2r.
S , 5 2pr ? h 5 40p → r ? h 5 20 → 2r 2 5 20 → r 5 10 cm
S T 5 2pr 2 1 2pr ? h 5 20p 1 40p 5 60p cm 2
127 A geratriz de um cilindro oblíquo mede 5 cm e forma com a base, que é um círculo de 2 cm de raio,
um ângulo de 458. Determine seu volume. 10p 2 cm 3
Resolução:
5
45°
2
h
128 Determine a área total de um semicilindro cujo raio da base mede 8 cm e a altura mede 12 cm.
(160p 1 192) cm2 Resolução:
8
12
ST
5
S,
2
1 Sretângulo 1 Sb
S, 2
5
2pr ? h
2
5 8p ? 12 5 96p cm
S 5 16 ? 12 5 192 cm retângulo 2
S b 5 8 2 p 5 64p
S T 5 96p 1 192 1 64p
S T 5 (192 1 160p) cm 2
sen 45° 5
h
5
2 5 2
→ h 5 cm
5 2
2
2 2
V 5 pr ? h 5 p2
?
2
5 2
2
3
5 10p 2 cm

129 Se o volume de um cubo é 8 m3 , determine o volume do cilindro nele inscrito.
Resolução:
130 (UEL-PR) O diretor de um clube deseja construir um poço, com formato cilíndrico, de 10,0 m de
profundidade e diâmetro interior igual a 1,0 m. Se a parede desse poço for construída com alvenaria na
espessura de 0,2 m, o volume dessa alvenaria será igual a:
a) 2,4p m3 c) 6,5p m3 e) 8,0p m3 b) 5,6p m3 d) 7,0p m3 Resolução:
p. 50
alvenaria
R 1
r
0,2
a 2r h
1
0,2
R 2
O cilindro inscrito no cubo é um cilindro eqüilátero.
V cubo 5 8 → a 3 5 8 → a 5 2 m
a 5 2r → 2 5 2r → r 5 1 m
a 5 h → h 5 2 m
V cilindro 5 S b ? h → pr 2 ? h 5 p ? 1 ? 2 5 2p m 3
10
cilindro maior → D 5 1,4; R 5 0,7 m
cilindro menor → d 5 1; r 5 0,5 m
V alvenaria 5 V C 2 V c 5 (0,7) 2 p ? 10 2 p ? (0,5) 2 ? 10 5 10p(0,49 2 0,25) 5 2,4p m 3
2p m 3
131 (FGV-SP) Considere uma lata de óleo de cozinha de formato cilíndrico que, originalmente, comportava
o volume de 1 litro de óleo e, atualmente, passou a comportar 0,9 litro. Assumindo-se log 0,95 5 0,5 e
0,9
admitindo-se que a altura da lata permaneceu a mesma, a redução percentual do raio de sua base foi igual a:
a) 6% c) 4% e) 2%
b) 5%
Resolução:
d) 3%
Sejam R o raio da lata inicial de 1 litro e R o raio da lata final de 0,9 litro.
1 2
V 5 p ? (R ) 1 1
H
H
2 ? h 5 1 ,
V 5 p ? (R ) 2 2 2 ? h 5 0,9 ,
Dividindo uma equação pela outra, temos:
2
⎛ R1
⎞
⎝
⎜
R ⎠
⎟ 5
1
0,9
5
10
9
→
R1
R
5 1,05 → R2 5 0,95R1
2
Portanto, houve uma redução de 5% no raio da base.
2

132 (Vunesp-SP) Se quadruplicarmos o raio da base de um cilindro, mantendo sua altura, o volume do
cilindro ficará multiplicado por:
a) 16 c) 8 e) 4p
b) 12 d) 4
Resolução:
V 5 pr2 ? h
Se quadruplicarmos o raio da base, obteremos:
V9 5 p(4r) 2 ? h 5 16pr2 ? h → o volume ficará 16 vezes maior.
133 (Unesp-SP) Considere uma lata cilíndrica de raio R e altura h completamente cheia de um
determinado líquido. Esse líquido deve ser distribuído totalmente em copos também cilíndricos cuja altura é
um quarto de altura da lata e cujo raio é dois terços do raio da lata. Determine:
2
a) os volumes da lata e do copo, em função de R e h V R h e V
1 2
lata 5 p copo 5 pR
h
9
b) o número de copos necessários, considerando que os copos serão totalmente cheios com líquido 9
Resolução:
a) V R
V
2
3 R
2
lata 5 p ? h
2
copo 5 p(
) ?
h
4
5
2
pR
? h
9
b) 5
? h
? h
9
5 9 5
Vlata
Vcopo
2
pR
pR
→
V 9V
2 lata copo
134 (Unicamp-SP) Um pluviômetro é um aparelho utilizado para medir a quantidade de
chuva precipitada em determinada região. A figura de um pluviômetro padrão é exibida. Nesse
pluviômetro, o diâmetro da abertura circular existente no topo é 20 cm. A água que cai sobre a
parte superior do aparelho é recolhida em um tubo cilíndrico interno. Esse tubo cilíndrico tem
60 cm de altura e sua base tem 1
da área da abertura superior do pluviômetro. (Obs.: a figura não
10
está em escala.)
a) Calcule o volume do tubo cilíndrico interno. 600p cm
b) Supondo que, durante uma chuva, o nível da água no cilindro interno subiu 2 cm, calcule o volume de
água precipitada por essa chuva sobre um terreno retangular com 500 m de comprimento por 300 m de
largura.
3
300 m3 Resolução:
Seja S a área da abertura superior.
R 5 10 cm
S 5 102p 5 100p cm2 S 5
1
2
S 5 10p 5 pr → r 5 10 cm
10
a) V 5 pr2 ? h 5 10p ? 60 5 600p cm3 b) Para uma área de captação de 100p cm2 , recolhe-se 10p ? 2 5 20p cm3 de água.
Para uma área de 500 m 3 300 m, temos a seguinte regra de três:
área volume
100p cm2 3 20p cm
1 500 000 000 cm2 V
8
15 ? 10 ? 20p
V 5
5 3 ? 10
100p
8 cm3 5 300 ? 106 cm3 5 300 m3

135 (FGV-SP) Inclinando-se em 45º um copo cilíndrico reto de altura 15 cm e raio de base 3,6 cm,
derrama-se parte do líquido que completava totalmente o copo, conforme indica a figura.
p. 55
Resolução:
7,2 cm
45°
45°
7,2 cm
Admitindo-se que o copo tenha sido inclinado com movimento
suave em relação à situação inicial, a menor quantidade de líquido
derramado corresponde a um percentual do líquido contido
inicialmente no copo de:
a) 48% d) 24%
b) 36% e) 18%
c) 28%
Como o ângulo é 45°, a menor quantidade de líquido derramado é a metade do volume de um
cilindro de mesma altura do diâmetro da base.
Vinicial
2
5 p(3,6)
? 15
Vderramado
5
1 2
p(3,6)
? 7,2
2
Vderramado
V
5
1 2
p(3,6)
? 7,2
2
2
p(3,6)
? 15
5 0,24
inicial
Ou seja, o líquido derramado corresponde a 24% do líquido inicial.
136 Dado um cone circular reto de raio da base 8 cm e altura 6 cm, determine:
a) a área lateral b) a área total 144p cm c) o volume
2
80p cm2 Resolução:
6
C
O
g 2 5 8 2 1 6 2 → g 5 10
8
g
A
a) S 5 pr ? g 5 8p ? 10 5 80p cm , 2
b) S 5 S 1 S 5 80p 1 p8 T , b 2 5 144p cm2 c) V 5
1
? Sb ? H 5
1
? 64 ? 6 5 128 cm
3
3
3
p p
128p cm 3

137 Uma ampulheta é formada por dois cones, conforme mostra a figura abaixo. Determine o volume de
areia necessário para encher completamente um dos cones. 20
3 cm3
p
10 cm
Resolução:
O cone possui raio 5 2 cm e altura 5 5 cm.
V 5
1
? Sb ? h 5
1 2 20p
3
p2
? 5 5 cm
3
3
3
138 (UFSC) A geratriz de um cone eqüilátero mede 2 3 cm. Calcule a área da secção meridiana do cone,
em centímetro quadrado, e multiplique o resultado por 3. 9
Resolução:
A secção meridiana de um cone eqüilátero é um triângulo eqüilátero.
A
r
V
h g 2r
O r
B
139 (UFMS) Considere um cone circular reto de volume V, com área da base igual a 16p cm2 . Calcule, em
centímetro cúbico, o valor de 3V
16p , sabendo-se que a área de uma secção feita no cone, paralela e distante
4 cm da base, é igual a 9p cm2 . 16
Resolução:
A
V
h
A B
9π
16π
0
2 cm
A área de um triângulo eqüilátero é dada por S 5 ,2 3
4
g 5 2r 5 2 3 → r 5 3 e , 5 2 3
S 5
2
2 ? 3 3
4
5 3 3 cm
3 3 ? 3 5 9
B
H
( )
H
h
2
2
16p
5
H
5
9p
h
→
h 5 H 2 4
H
H 2 4
4
3
5
4
→ 4H 2 16 5 3H → H 5 16
3
V 5
1
3
? 16p
? 16
3V
16p
5
3 ?
1
? 16p
? 16
3
16p
5 16
.

140 (ITA-SP) As medidas, em metro, do raio da base, da altura e da geratriz de um cone circular reto
formam, nessa ordem, uma progressão aritmética de razão 2 m. Calcule a área total desse cone em metro
quadrado. 96p m2 141 O que ocorrerá com o volume de um cone de revolução, se duplicarmos sua altura?
142 (Unesp-SP) Um recipiente tampado, na forma de um cone circular reto de altura 18 cm e raio 6 cm,
contém um líquido até a altura de 15 cm (figura 1). A seguir, a posição do recipiente é invertida (figura 2).
18 cm
Resolução:
h
Resolução:
raio 6 cm raio R
Sendo R e r os raios mostrados nas figuras:
figura 1
O
15 cm
V
H
r
g
figura 2
A
V 5
1
3
? Sb ? h
V 9 5
1
3
? Sb ? (2h) 5 2 ?
1
3
? Sb ? h 5 2V → o volume dobrará.
Resolução:
a)
( ) ( )
2 2
raio r
h 2 r 5 g 2 h 5 2
g 2 5 h 2 1 r 2
(h 1 2) 2 5 h 2 1 (h 2 2) 2
h 2 1 4h 1 4 5 h 2 1 h 2 2 4h 1 4 → h 2 2 8h 5 0 → h ? (h 2 8) 5 0 →
→ h 5 0 (não convém) ou h 5 8
Então: h 2 r 5 2 → 8 2 r 5 2 → r 5 6 m
g 2 h 5 2 → g 2 8 5 2 → g 5 10 m
S T 5 S b 1 S ,
S T 5 p6 2 1 p ? 6 ? 10 5 96p m 2
36
25
6 2
18
15
5
S
s
→
6
5
5
S
s
→ 5
p
s
→ s 5 25p cm
2
s 5 pR 5 25p → R 5 5 cm
O volume dobrará.
a) determine R e o volume do líquido no cone em centímetro
cúbico (figura 1), como múltiplo de p.
3
b) dado que r 5 91,
determine a altura H da parte sem
3
líquido do cone na figura 2. Use a aproximação 91
9
( 5 .
2 ) 27
2 cm
R 5 5 cm e V 5 125p cm3 V 5
1 2
3
p5 ? 15 5 125p cm
3
2
b)
H ( 18 ) 5
2
pr
→
36p
H
18
5
r
6
→
H
18
5
3
91
6
→
H
18
5
9
2
6
→ H 5
27
2 cm
2

143 (Unesp-SP) Um recipiente, na forma de um cilindro circular reto de raio R e altura 32 cm, está até a
metade com água (figura 1). Outro recipiente, na forma de um cone circular reto, contém uma substância
química que forma um cone de altura 27 cm e raio r (figura 2).
a) Sabendo que R 5 r,
raio R
raio r
32 cm
água 27 cm h mistura
figura 1 figura 2
(substância química)
figura 3
3 ( 2 ) determine o volume da
água no cilindro e o volume da substância química
no cone, em função de r. (Para facilitar os cálculos,
use a aproximação p 5 3.) 108r
b) A substância química do cone é despejada no
cilindro, formando uma mistura homogênea (figura
3). Determine a concentração (porcentagem) da
substância química na mistura e altura h atingida
pela mistura no cilindro.
2 cm3 e 27r2 cm3 Resolução:
20% e 20 cm
a) Sejam V o volume do cilindro inicial, V o
1 2
volume do cone e V o volume do cilindro
com a mistura.
2
V1 5 pR ? 1,6; R 5
3
r →
2
b) V 5 V 1 V 1 2
V 5 108r
→ V1
V2
5
9 2 2 3
5 p r ? 16 5 108r cm
4
1 2 2 3
p r ? 27 5 27r cm
3 2 1 27r2 5 135r2 cm3 V
2
2 5
27r
5
1
5 20%
2 V 135r 5
pR2 ? h 5 135r2 2
p
3
2
( r 135r
2 ) ? h 5 → h 5 20 cm
144 (Unifesp-SP) A figura representa um lápis novo e sua parte
apontada, sendo que D, o diâmetro do lápis, mede 10 mm; d, o diâmetro
da grafite, mede 2 mm; e h, a altura do cilindro reto que representa a parte
apontada, mede 15 mm. A altura do cone reto, representando a parte da
grafite que foi apontada, mede 5 mm.
0,25p cm
a) Calcule o volume do material (madeira e grafite) retirado do lápis.
b) Calcule o volume da grafite retirada.
3
2 ? 1023p cm3 Resolução:
1,5 cm h
h
lápis lápis
D
d
grafite
h
O
A
B
C D
OB 1 mm 0,1 cm
CD 6 mm 0,5 cm
1,5 cm h
a) D 5 10 mm → R 5 5 mm 5 0,5 cm
volume do material retirado: V 5 V 2 V 1 cilindro cone
V1 2
5 p(0,5) ? 1,5 2
1
2
p ? (0,5) ? 1,5 5
3
2
2
p ? (0,5) ? 1, 5
3
0,25 cm 3
5 p
b) V 5 V 1 V grafite cilindro cone
altura da grafite: AO
AC
5
OB
CD
→
h9
1,5
5
0,1
0,5
→ h9 5 0,3 cm
V grafite
2
5 p(0,1) ? 0,3 2
1
2
p ? (0,1) ? 0, 3 5
3
2
? (0,1)
3
? 0,3 5 2
2
? 10 cm
3
p p
2 3
h
D
d
grafite
lápis lápis

p. 56
145 (Fuvest-SP) Um torneiro mecânico dispõe de uma peça de metal
maciça na forma de um cone circular reto de 15 cm de altura e cuja base B
tem raio 8 cm (figura 1). Ele deverá furar o cone, a partir de sua base, usando
uma broca, cujo eixo central coincide com o eixo do cone. A broca perfurará
a peça até atravessá-la completamente, abrindo uma cavidade cilíndrica, de
modo que se obtenha o sólido da figura 2. Se a área da base desse novo sólido
é 2
640
9
cm 3
3 p
3 da área de B, determine seu volume. figura 1 (antes) figura 2 (depois)
Resolução:
Sejam S a área da base do sólido inicial de raio R e r o raio do cilindro retirado.
De acordo com o enunciado, temos:
2 2
p8 2 pr 5
2 2 2
p ? 8 → 5
64 8 3
r → r 5 cm
3
3
3
h
H
5
r
→
h
5
R 15
146 (UFSCar-SP) Em uma lanchonete, um casal de namorados resolve dividir uma
taça de milk shake com as dimensões mostradas no desenho.
a) Sabendo que a taça estava totalmente cheia e que eles beberam todo o milk shake,
calcule qual foi o volume, em milímetro, ingerido pelo casal. (Adote p 5 3.) 500 cm
b) Se um deles beber sozinho até a metade da altura do copo, quanto do volume total,
em porcentagem, terá bebido?
3
87,5%
Resolução:
a) V 5
1
3
? Sb ? H → r 5 5 cm 5 50 mm; h 5 20 cm 5 200 mm
V 5
1
2
3
p ? 50 ? 200 5 500 000
mm
3
3
5 500 cm
b) Seja V 1 o volume do cone de altura 10 cm.
V cheio 5 V 2 V 1
8 3
3
8
→ h 5 5 3 cm
B C
V 5 volume do cone inicial: R 5 8, H 5 15 → V
1 1 5
1 2
p ? 8 ? 15
3
r
8
V 5 volume do cilindro de raio r e altura 5 ( 15 2 5 3 ) → 2 V2 2
⎛ 8 3 ⎞
5 p
⎝
? 15 2 5 3
3 ⎠ ( )
V 5 volume do cone eliminado → V 3 3 5
volume procurado: V 5 V 2 V 2 V 1 2 3
1 ⎛ 8 3 ⎞
p ?
3 ⎝ 3 ⎠
? 5 3
V 320 320 3 3 cm 3
5 p 2 p 1
320
3
p 2
1
9
? 320 p 5
640
9
3 p
S
S
10
20
2
S
5
20
s ( 10 ) →
? r9
p
2
5
p ( )
V cheio
V
V
cheio
2
( )
5 4 → r9
5
5 500 2
1 750
1
p ?
3
5
2
? 10 5
5 4
500
5 87,5%
2
2
5
2
1 750
4
D
A
10 cm
h
E
15
20 cm

147 (Mackenzie-SP) No sólido da figura, ABCD é um quadrado de lado 2 e
AE 5 BE 5 10. O volume desse sólido é:
a) 5p
2
c) 4p e) 3p
b) 4p
3
Resolução:
d) 5p
D
2
A
p. 60
148 Calcule a área lateral, a área total e o volume do tronco de cone descrito abaixo:
h
r
R
g
Resolução:
S 5 pg ? (R 1 r)
,
g2 5 h2 1 (R 2 r) 2
g2 5 21 1 22 5 25 → g 5 5
S 5 p ? 5 ? (6 1 4) 5 50p cm , 2
S 5 S 1 S 1 S T , B b
S 5 50p 1 p6 T 2 1 p42 5 102p cm2 VT 5
hp
2 2
? (R 1 R ? r 1 r )
3
V
10
T
2
E
h
10
C
B
h 2 2
2
1 1 5 ( 10 ) → h 5 3
V 5 V 1 V
V
cilindro cone
2
5 p ? 1 ? 1
1 2
2 p ? 1 ? 3 5 3p
3
h 5 21 cm
r 5 4 cm
R 5 6 cm
5
21p
76 21p
? (36 1 24 1 16) 5
3
3
cm 3
S , 5 50p cm 2 ; S t 5 102p cm 2 e V
D
A
E
76 21
5
3
p
C
B
cm 3

149 Um tronco de cone tem altura igual a 8 m e os raios das bases, 3 m e 9 m, respectivamente.
Determine a área total e o volume. S 5 210p m t 2 e V 5 312p m3 Resolução:
S 5 pg ? (R 1 r)
,
g2 5 h2 1 (R – r) 2
g2 5 82 1 62 5 100 → g 5 10 m
S 5 p ? 10 ? (9 1 3) 5 120p m , 2
S 5 S 1 S 1 S T , B b
S 5 120p 1 p9 T 2 1 p ? 32 5 210p m2 VT 5
hp
2 2
? (R 1 R ? r 1 r )
3
VT
5
8p
? (81 1 27 1 9) 5 312p m
3
150 Em um tronco de cone de revolução os raios das bases e a altura medem, respectivamente, 3 m, 6 m
e 12 m. Determine sua área total. 45p 1 27p
17 m 2
Resolução:
S , 5 pg ? (R 1 r)
g 2 5 h 2 1 (R 2 r) 2
( )
2 2 2
g 5 12 1 3 5 153 → g 5 3 17 m
S 5 3 p 17 ? (6 1 3) 5 27p 17 m
,
S T
5 S 1 S 1 S
,
h
B
r
R
b
g
h 5 8 m
r 5 3 m
R 5 9 m
ST
5 27p 17 1 36p 1 9p 5 45p 1 27p 17 m
2
3
( )
151 Determine o raio da base menor de um tronco de cone, sendo o raio maior o dobro do menor, a
1 792p
3
altura o dobro do raio maior e o volume igual a cm . 4 cm
3
Resolução:
4r
r
2r
2
VT 5
hp
3
2
2
? (R 1 R ? r 1 r )
1 792p
3
5
4pr 3
2
? (4r
2
1 2r
2
1 r ) 5
3
28r p 3
→ r 5 64 → r
5 4 cm
3

152 Uma secção transversal de um cone circular de 20 cm de altura dista 5 cm da base e tem área igual a
12p cm2 . Determine o volume do tronco limitado por esse plano. 740
cm
9
3 p
Resolução:
A
V
15 cm
A
12π
B
5 cm
B
VT 5
hp
2
? (R 1 R ? r 1 r )
3
SB
5
12p
→
2
2
20
16
SB
( 15 ) 5 SB
9 12p 5
64
3
SB 2
5 R 5
64
R 5
3
8 3
3
cm
Sb
5 12 5
→
p
p
p
→
2
p pr → r 5 2 3 cm
5p
740p
VT 5 ?
64
3
1 1 5 cm
3 ( 16 12
3
) 9
153 Os raios das bases de um tronco de cone são 10 cm e 12 cm. Qual o raio do cone de mesma altura e
de mesmo volume do tronco de cone? 2 91 cm
Resolução:
10
h h
12
R
VT 5
hp
3
2
2
? (R 1 R ? r 1 r )
Vc 5
1 2
pR
? h
3
VT 5 Vc
→ p h
3
2
? (R
2
1 R ? r 1 r ) 5
1 2 2
pR ? h → 12 1 120
3
1 10
2
5 R → R 5
2
2 91 cm
154 (Fuvest-SP) As bases de um tronco de cone circular reto são círculos de raios 3 cm e 6 cm. Sabendo
que a área lateral do tronco é igual à soma das áreas das bases, calcule:
a) a altura do tronco de cone 4 cm b) o volume do tronco de cone 84p cm3 Resolução:
h
r
R
g
r 5 3 cm
R 5 6 cm
S 5 S 1 S , B b
pg ? (R 1 r) 5 pr2 1 pR2 g ? (3 1 6) 5 32 1 62 → g 5 5 cm
a) h2 5 g2 2 (R 2 r) 2 → h2 5 25 2 9 5 16 → h 5 4 cm
b) V
h
2
T 5
p 2
? (R 1 R ? r 1 r )
3
4
2
VT
5
p 2
? (6 1 6 ? 3 1 3 ) 5 84p
cm
3
3

155 (Mackenzie-SP) Uma xícara de chá tem a forma de um tronco de cone reto, conforme a figura.
6 cm
Supondo p 5 3, o volume máximo de líquido que ela pode conter é:
a) 168 cm3 c) 166 cm3 e) 164 cm3 b) 172 cm3 d) 176 cm3 Resolução:
R 5 4 cm; r 5 2 cm; h 5 6 cm
VT
5
hp
3
2
? (R
2
1 R ? r 1 r )
VT
5
6p
3
2
? (4
2
3
1 4 ? 2 1 2 ) 5 168 cm
8 cm
4 cm
156 (Unicamp-SP) Um abajur de tecido tem a forma de um tronco de cone reto, com bases paralelas. As
aberturas do abajur têm 25 cm e 50 cm de diâmetro, e a geratriz do tronco de cone mede 30 cm. O tecido do
abajur se rasgou e deseja-se substituí-lo.
a) Determine os raios dos arcos que devem ser demarcados sobre um novo tecido para que se possa cortar
um revestimento igual àquele que foi danificado. 30 cm e 60 cm
b) Calcule a área da região a ser demarcada sobre o tecido que revestirá o abajur. 1 125p cm2 Resolução:
a) Os raios que devem ser demarcados sobre o tecido são o do cone maior, G, e o do cone menor, g.
Os triângulos AOD e ABC são semelhantes, logo:
25
g g
5
r
→ 5
2
→ g 5 30 cm → G 5 60 cm
G R g 1 30 25
b) S 5 pg9 ? (R 1 r) 5 30p ? T 25
1 25
2
A
O r
C
( ) 5 1 125p cm 2
g
R
D
30
G
B

157 (FGV-SP) Um tronco de cone circular reto foi dividido em quatro partes iguais idênticas por planos
perpendiculares entre si e perpendiculares ao plano da sua base, como indica a figura.
vista superior
de 1 do tronco
4
4 cm
6 cm
Se a altura do tronco é 10 cm, a medida de sua geratriz, em centímetro, é igual a:
a) 101 c) 103 e) 105
b) 102
Resolução:
d) 2 26
p. 65
R
6
4
Cálculo dos raios do tronco:
2
r 1
2
r
2
5 4 → r 5 2 2 cm
2
R 1
2
R
2
5 6 → R 5 3 2 cm
r
158 Qual o volume de uma bola de futebol cujo diâmetro é 20 cm?
Resolução:
V 5
4 3
pR
3
R 5 10 cm
V 5
4
p10
3
5
4 000p cm
3
3 3
4 000p
3
159 Determine o volume de uma esfera circunscrita a um cubo de aresta 5 cm.
Resolução:
5
10 g
cm 3
2 2
3 2
2
g
2
2
1 10 1 (R 2 r)
2
g
2
5 10 1 (
2
2 ) 5 100 1 2 → g 5 102 cm
125p
3
2
O raio da esfera é a metade da diagonal do cubo.
R 5
5 3
2
V 5
4 3
pR 5
3
3
4 ⎛ 5 3 ⎞
p ? 5
3 ⎝
⎜ 2 ⎠
⎟
4
p ?
3
125 ? 3 ?
8
3
cm 3
125p
3
5
2
3
cm

160 A área de uma superfície esférica é 100p cm 2 . Determine seu volume.
Resolução:
2
S 5 4pR 5 100p → R 5 5 cm
V 5
4 3
pR 3
→
4 3
p5
5
3
500p
3
cm
3
500
3
p
161 Uma bola maciça de madeira tem raio 4 cm, e uma outra bola também maciça tem diâmetro 5 vezes
maior que o diâmetro da primeira. Qual a razão entre os volumes das bolas? v
5
1
V 125
Resolução:
v r
3 4
5
4 3
p 5
3
4 3
p
V 5
4 3
pR 5
3
4
3
p ? (5 ? 4)
3
v
V 5
4 3
p4
3
4 3 3
p5
? 4
3
→
v
V
5
1
125
162 (UFRGS) No desenho abaixo, em cada um dos vértices do cubo está centrada uma esfera cuja medida
do diâmetro é igual à medida da aresta do cubo.
A razão entre o volume da porção do cubo ocupado pelas esferas e o volume do cubo é:
a) p
6
p
c)
4
p
e)
2
b) p
5
p
d)
3
Resolução:
Cada esfera ocupa 1
de seu volume no cubo. Como o cubo possui 8 vértices, temos: V
8
A aresta do cubo é 2R, portanto: V 5 (2R) c 3 .
V
V
4
3 R
e 5
3
p
3
8R
5
p
6
c
cm 3
e
4
3 R
3
5 p .

163 (UFPel-RS) O jogo de bochas foi trazido para o Rio Grande do Sul provavelmente pelos italianos e
não é muito antigo em nosso estado, porém de profunda aceitação em todas as regiões.
No Sul, as canchas mais comuns possuem pisos de terra batida ou madeira, apresentando dimensões de
24 m de comprimento e 4 m de largura. Cada bola desse jogo possui diâmetro de 10 cm.
A partir do texto e de seus conhecimentos, e considerando p 5 3,14, determine:
a) a área da superfície esférica correspondente a uma bola de bocha;
b) o volume da esfera que corresponde a uma bola de bocha; 523,33 cm
c) o maior número de bolas de bocha que se pode guardar em uma caixa de madeira em forma de
paralelepípedo retângulo de dimensões internas 45 cm, 40 cm e 20 cm.
3
314 cm2 Resolução:
R 5 5 cm
a) S 5 4pR
32 bolas
2 5 4p52 5 100p 5 314 cm2 b) V
4
3 R 5
3
p 5
4 3 3
pR
5 523,33 cm
3
c) Sendo o diâmetro de cada bola 10 cm, podemos colocar 4 bolas em 45 cm, 4 bolas em 40 cm e 2
bolas em 20 cm. Portanto: 4 ? 4 ? 2 5 32 bolas na caixa.
164 (Unifesp-SP) Um inseto vai se deslocar sobre uma superfície esférica de raio 50 cm, desde um ponto
A até um ponto B, diametralmente opostos, conforme a figura.
O menor trajeto possível que o inseto pode percorrer tem comprimento igual a:
B a) p
m
2
3
c)
2 m
p
e) 3p m
b) p m d) 2p m
A
O
Resolução:
O menor trajeto é a metade da circunferência do círculo máximo da esfera.
C 5
1
? 2pR 5 50p 5 50p cm 5 0,50p m
2
165 (Mackenzie-SP) Um recipiente cilíndrico reto, com raio da base igual a 4 cm, contém água até a
metade de sua altura. Uma esfera maciça, colocada no seu interior, fica totalmente submersa, elevando a
altura da água em 2 cm. O raio da esfera é:
a) 3
2 3
c) 3
3 2
e) 2
b) 4 d)
Resolução:
2
3
5
2
O volume da esfera é igual ao volume de água deslocado.
V 5 pr c 2 ? h 5 16p ? 2 5 32p
V
4 3 3 3
e 5 pR 5 32p → R 5 24
→ R 5 2 3
3
0

166 (Mackenzie-SP) Uma esfera de raio R é cortada por dois planos paralelos, um deles passando por seu
centro, obtendo-se, assim, dois círculos cujas áreas estão na razão de 1 para 4. A distância d entre os dois
planos, em função de R, é:
a) d 5
2R
3
c) d
b) d 5
R
2
Resolução:
d) d 5
p. 66
d
O
C R
r
R
A
R 3
5 e) d 5 R 2
2
R 3
3
2
pr
2
pR
5
1
4
2
→ r 5
2
R
4
2
d
2
5 R
2
2 r
2
5 R 2
R
4
d 5
R 3
2
167 (Mackenzie-SP) Uma bóia marítima construída de determinada liga metálica tem o formato
de uma gota que, separada em dois sólidos, resulta em um cone reto e em uma semi-esfera,
conforme a figura ao lado, na qual r 5 50 cm. Se o preço do metro quadrado da liga metálica é
1 200 reais, adotando-se p 5 3, o custo da superfície da bóia é, em reais, igual a:
a) 4 200 c) 4 500 e) 3 800
b) 5 700
Resolução:
S 5 S 1 S T lateral do cone meia esfera
d) 5 200
S 5 pr ? T g 1
2
4 r
2
p 5 3 ? 50 ? 3 ? 50 1 2 ? 3 ? 502 5 37 500 cm2 5 3,75 m2 custo 5 1 200 ? 3,75 5 R$ 4 500,00
168 (Fatec-SP) Duas esferas maciças iguais e tangentes entre si estão inscritas em um
paralelepípedo reto-retângulo oco, como mostra a figura. Observe que cada esfera tangencia
as quatro faces laterais e uma das bases do paralelepípedo.
O espaço entre as esferas e o paralelepípedo está preenchido com um líquido. Se a aresta
da base do paralelepípedo mede 6 cm, o volume do líquido nele contido, em litro, é
aproximadamente igual a:
a) 0,144 c) 1,44 e) 20,6
b) 0,206 d) 2,06
Resolução:
6
6
12
V 5 V 2 2V líquido prisma esfera
V 5 6 ? 6 ? 12 5 432 cm prisma 3 5 0,432 dm3 Vesfera 5
4 3
5
4 3 3
pr p3 5 36p 5 113,04 dm
3 3
V 5 0,432 2 2 ? 113,04 5 0,432 2 0,226 5 0,206 dm líquido 3
2
r
r

169 (UFU-MG) Todos os tanques de armazenamento de combustível de uma refinaria possuem o mesmo
formato de um cilindro circular reto de 20 m de altura com capacidade individual de armazenamento de
2 000p m3 de gasolina. Suponha que de um desses tanques totalmente cheio de gasolina foi retirada uma
quantidade desse combustível suficiente para encher, totalmente, 30 caminhões-tanque usados na distribuição
para alguns postos de combustíveis. Sabendo que os tanques dos caminhões são idênticos e possuem a forma de
um cilindro circular reto de 5 m de comprimento com um hemisfério em cada extremidade de raio 1 m, conforme
figura abaixo, determine a altura atingida pela gasolina restante no tanque cilíndrico do depósito. 18,10 m
p. 70
Resolução:
1 m
20 m
5 m 1 m
tanque dos caminhões tanque de armazenamento
Vcaminhão
5 Vcilindro 1 Vesfera
Vcaminhão
2
5 p ? 1 ? 5 1
4 2
p ? 1 5
19p 3
3
3
m
Vgasolina 5 Vtanque
2 30Vcaminhão 5 2 000p 2 30 ?
19p
3
5 1 810p m
V 5 S ? H 5 S ? 20 5 2 000p → S 5 100p
tanque
V 5 1 810p m
gasolina
b b b
3
1 810p
5 Sb
? h → h 5 5 18,10 m
100p
170 Um poliedro possui 20 arestas e 10 faces. Qual o número de vértices?
Resolução:
A 5 20; F 5 10
V 2 A 1 F 5 2
V 2 20 1 10 5 2
V 5 12
171 Um poliedro possui 20 faces e 42 arestas. Qual a soma dos ângulos de todas as faces desse poliedro? 7 920°
Resolução:
F 5 20; A 5 42
S 5 (V 2 2) ? 4r
V 2 A 1 F 5 2
V 2 42 1 20 5 2 → V 5 24
S 5 (24 2 2) ? 360° 5 22 ? 360° 5 7 920°
172 Um poliedro possui 6 ângulos triédricos e 4 ângulos tetraédricos. Qual o número de arestas, vértices
e faces? V 5 10; A 5 17 e F 5 9
Resolução:
A 5 ? 1 ? 6 3 4 4
5 9 1 8 5 17
2 2
V 5 6 1 4 5 10
V 2 A 1 F 5 2
10 2 17 1 F 5 2 → F 5 9
3
12

173 Um poliedro é constituído por 12 faces triangulares. Quantos vértices ele possui?
Resolução:
12 ? 3
F 5 12; A 5 5 18
2
V 2 A 1 F 5 2
V 2 18 1 12 5 2 → V 5 8
174 Qual é o poliedro que se obtém unindo-se os centros de um hexaedro regular?
Resolução:
175 Calcule a soma dos ângulos das faces de um:
a) dodecaedro; 6 480°
b) icosaedro.
Resolução:
S 5 (V 2 2)4r
a) dodecaedro: V 5 20 → S 5 18 ? 4 ? 90° 5 6 480°
b) icosaedro: V 5 12 → S 5 10 ? 4 ? 90° 5 3 600°
3 600°
octaedro
176 Um poliedro tem 3 faces quadrangulares, 2 faces triangulares e 4 faces pentagonais. Determine a
soma dos ângulos das faces desse poliedro. 3 600°
Resolução:
F 5 3 1 2 1 4 5 9
A 5 ? 1 ? 1 ? 3 4 2 3 4 5
5 19
2
V 2 A 1 F 5 2 → V 2 19 1 9 5 2 → V 5 12
S 5 (V 2 2) ? 4r → S 5 10 ? 4 ? 90° 5 3 600°
Um hexaedro regular é um cubo.
Unindo-se os centros das faces, temos um octaedro regular.
8

177 A soma das medidas dos ângulos das faces de um poliedro é 4 3208. Qual a sua natureza, sabendo que
ele é um prisma? prisma heptagonal
Resolução:
2 ? (n 2 2) ? 180° 1 360°n 5 4 320°
360°n 2 720° 1 360°n 5 4 320°
720°n 5 5 040
n 5 7
A base do prisma é um heptágono.
178 Um poliedro convexo de 39 arestas possui faces triangulares e pentagonais. Quantas faces de cada
tipo ele tem, sabendo que a soma é 68 ângulos retos? 16 faces triangulares e 6 faces pentagonais
Resolução:
Sejam n o número de faces triangulares e m o número de faces pentagonais.
F 5 n 1 m
3n 1 5m
A 5
5 39
2
S 5 (V 2 2) ? 4r 5 68r → V 5 19
V 2 A 1 F 5 2 → 19 2 39 1 F 5 2 → F 5 22
Então, temos o sistema
179 Quantas arestas e vértices possui o dodecaedro de Platão?
Resolução:
3n 1 5m 5 78
n 1 m 5 22 3( 23)
3n 1 5m 5 78
23n 2 3m 5 266
→
⎧
⎨
⎩
⎧
⎨
⎩
2m 5 12 → m 5 6
Substituindo m, temos:
n 1 6 5 22 → n 5 16
Portanto, são 16 faces triangulares e 6 faces pentagonais.
A 5
12 ? 5
5
2
30
A 5 30; V 5 20
F 5 12
V 2 A 1 F 5 2 → V 5 2 1 30 2 12 5 20

180 (Unifesp-SP) Considere o poliedro cujos vértices são os pontos médios das arestas de um cubo.
O número de faces triangulares e o número de faces quadradas desse poliedro são, respectivamente:
a) 8 e 8 c) 6 e 8 e) 6 e 6
b) 8 e 6 d) 8 e 4
Resolução:
• cada face triangular está associada a um vértice do cubo; portanto, temos 8 faces triangulares.
• cada face quadrada está contida numa face do cubo; portanto, temos 6 faces quadradas.
181 Qual é o poliedro determinado pelos pontos médios das arestas de um tetraedro regular? octaedro
Resolução:
O poliedro determinado pelos pontos médios das arestas de um
tetraedro regular é um octaedro regular.