11 CAS i GeoGebra

11 CAS i GeoGebra
Fra og med versjon 4.2 får GeoGebra et eget CAS-vindu. CAS står for Computer Algebra
System og er en betegnelse for programvare som kan gjøre symbolske manipuleringer. Eksempler
på slike manipuleringer er å løse likninger med rotutdragning (eksakte verdier),
faktorisering av polynomer, integrering og derivering, beregning av summer osv.
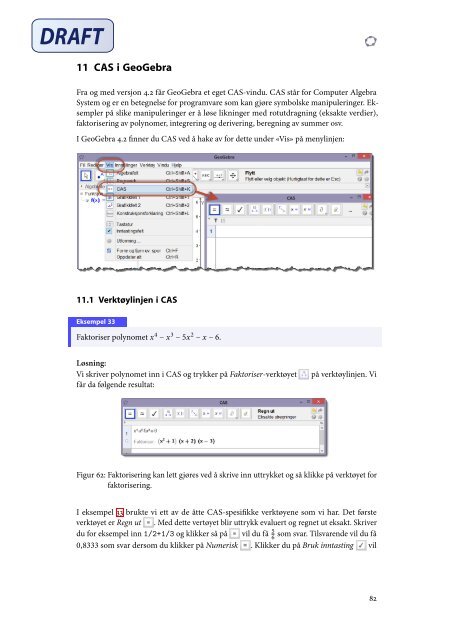
I GeoGebra 4.2 finner du CAS ved å hake av for dette under «Vis» på menylinjen:
11.1 Verktøylinjen i CAS
Eksempel 33
Faktoriser polynomet x 4 − x 3 − 5x 2 − x − 6.
Løsning:
Vi skriver polynomet inn i CAS og trykker på Faktoriser-verktøyet
får da følgende resultat:
på verktøylinjen. Vi
Figur 62: Faktorisering kan lett gjøres ved å skrive inn uttrykket og så klikke på verktøyet for
faktorisering.
I eksempel 33 brukte vi ett av de åtte CAS-spesifikke verktøyene som vi har. Det første
verktøyet er Regn ut . Med dette vertøyet blir uttrykk evaluert og regnet ut eksakt. Skriver
du for eksempel inn 1/2+1/3 og klikker så på vil du få 5 6
som svar. Tilsvarende vil du få
0,8333 som svar dersom du klikker på Numerisk . Klikker du på Bruk inntasting vil
82

11.1 Verktøylinjen i CAS
det ikke bli gjort noe med uttrykket du har skrevet inn. I eksempelet med 1/2+1/3 vil vi få
som svar.
1
2 + 1 3
Figur 63: Du får ulike output alt etter som hvilket verktøy som er valgt.
Merk at du kan enten skrive inn uttrykket og så klikke på ett av disse verktøyene beskrevet
over eller du kan aktivere verktøyet, skrive inn uttrykket og så trykke . Har du for
eksempel aktivert Numerisk og skriver inn 4/7 vil du få 0,5714 som svar.
Neste verktøy på verktøylinjen er Faktoriser . I eksempel 33 brukte vi dette til å faktorisere
et polynom. Du kan selvsagt også bruke dette til å faktorisere hele tall.
Figur 64: Faktorisering av hele tall i GeoGebra.
Går vi ett hakk til høyre på verktøylinja finner vi verktøyet Utvid
GeoGebra om å multiplisere ut parenteser etc.
. Vi bruker dette til å be
Eksempel 34
Gang ut (a + b) 5
Løsning:
Vi skriver inn (a+b)^5 og klikker på :
83

11.1 Verktøylinjen i CAS
Figur 65: Det kan ta litt tid å gange ut (a + b) 5 dersom du ikke kan binomialteoremet...
Neste verktøy er Sett inn
variable eller tall.
. Med dette kan du erstatte én eller flere variable med andre
Eksempel 35
Skriv inn formelen F = m ċ a i CAS finn a når F = 12 og m = 55.
Løsning:
Vi skriver inn F=m*a og klikker på
substitusjonene:
. Vi får da opp et vindu der vi kan skrive inn de ønskede
Figur 66: Vi bytter ut F med 12 og m med 55 ved å bruke Sett inn-verktøyet
Klikker vi på får vi svaret 12 = 55a. Vi løser denne likningen ved å bruke verktøyet Løs
. For å bruke dette må vi hente opp forrige output og så klikke på . Du kan lett kopiere
inn siste output ved å trykke på space-baren på tastaturet. Klikk deretter på (Løs) og får
a = 12
55
. Dersom vi ønsker desimaltall trykker vi på mellomromstasten en gang til og så på
.
84

11.1 Verktøylinjen i CAS
Figur 67: Vi har funnet at a ≈ 0,22 når F = 12 og m = 55.
Helt til høyre på verktøylinja ligger det to verktøy: Derivert og Integral . For å bruke
disse er det bare til å skrive inn et uttrykk og klikke på verktøyet. Uttrykket du skriver inn
behøver ikke å være et uttrykk i x. Men dersom du skriver inn a 4 b 2 , så vil GeoGebra derivere
med hensyn på a. Mer generelt, så vil GeoGebra derivere/integrere med hensyn på den første
av varbiablene i lista x, y, z, a, b, ...v, w som er uttrykket inneholder.
Oppgave 55
a) 2 + 13 3 − 12 ċ 43
b) 122
9
Figur 68: Derivering og integrering i CAS.
Bruk CAS til å regne ut
c)
2 +
6
2 + 3
Oppgave 56 Gang ut: (a + b + c) 3 .
Oppgave 57 Finn de eksakte røtten til likningen x 3 + 8x 2 − 2x − 16 = 0
85

11.2 CAS-kommandoer
Oppgave 58
Oppgave 59
Deriver funksjonen f(x) = x 4 ln(x).
Finn integralet ∫ x 4 ċ sin(2x) dx
11.2 CAS-kommandoer
Vi har så langt sett hvordan vi kan bruke CAS-verktøyene til å utføre ulike operasjoner på
uttrykk. Dersom vi kikker godt etter, ser vi at til de fleste verktøyene har en tilhørende kommando.
Når vi utvidet (a+b) 5 ved å bruke Utvid ser vi at dette verktøyet kjører kommandoen
RegnUt.
Figur 69: Verktøyet Utvid kjører kommandoen RegnUt
I stedet for å bruke verktøyet Utvid kunne vi med andre ord kjørt kommandoen RegnUt
direkte:
Figur 70: Du kan utvide parenteser ved å direkte bruke kommandoen RegnUt
Det fins godt over 100 slike kommandoer i GeoGebra og du finner dem alle på nettsiden
http://wiki.geogebra.org/nb/CAS_Spesielle_kommandoer. Vi har listet opp et utvalg
kommandoer i tabell 2 på neste side.
86

11.2 CAS-kommandoer
Kommando
Binomialkoeffisient[a, b]
Delbrøkoppspalting[]
Derivert[]
Derivert[, ]
Derivert[, ,n]
Faktoriser[]
Kryssprodukt[{a,b,c},{d,e,f}]
Løsninger[likninger, ]
Nevner[]
NLøs[]
NLøs[, ]
Nløsninger[, ]
Nullpunkt[
Prikkprodukt[ , ]
Sum[, , a, b]
Forklaring
Regner ut a b
Gir
delbrøksoppspaltningen
(om mulig) til funksjonen.
Gir den deriverte til
uttrykket.
Gir den deriverte til
uttrykket med hensyn på
variabelen.
Gir den n-te deriverte til
uttrykket med hensyn på
variabelen.
Faktoriserer uttrykket.
Regner ut vektorproduktet
[a, b, c] × [d, e, f].
Løser likningssystemet i
de oppgitte variablene.
Gir nevneren eller
fellesnevneren til
uttrykket.
Finner en numerisk
løsning til likningen.
Finner en numerisk
løsning til likningen med
hensyn på variabelen.
Finner en numerisk
løsning av
likningssystemet i de
oppgitte variablene.
Finne nullpunktene til
polynomet.
Gir prikkproduktet
mellom vektorene.
Regner ut b a (uttrykk)
Tabell 2: Et utvalg av kommandoer du kan bruke i CAS
Eksempel 36
Faktoriser polynomet 2x 3 + 3x 2 − 32x + 15.
87

11.2 CAS-kommandoer
Løsning:
Vi skriver inn Faktoriser[2x^3+3x^2-32x+15] og trykker enter. Vi får at
2x 3 + 3x 2 − 32x + 15 = (2x − 1)(x + 5)(x − 3)
Eksempel 37
Løs likningen sin(x) + cos(x) = 1.
Løsning:
Vi skriver inn kommandoen Løs[sin(x)+cos(x)=1] og får:
Merk at GeoGebra bruker radianer som vinkelmål i CAS. Ønsker du å løse likningen med
grader som vinkelmål må du skrive x ∘ som vist på figuren over.
Vi ser at x = 2π ċ n + π 2
eller x = 2nπ.
Eksempel 38
Finn eventuelle topp- eller bunnpunkter til grafen til f(x) = xe x .
Løsning:
Vi kan definere en funksjon i CAS ved å skrive inn
f(x):=x*e^x
Vi bruker kolon foran likhetstegnet når vi definerer en funksjon i CAS. Du kan selvsagt også
definere funksjonen på vanlig måte i inntastingsfeltet før du jobber videre med den i CAS. I
så tilfelle skriver du kun inn f(x)=x*e^x i inntastingsfeltet.
Når funksjonen er definert kan vi skrive inn Løs[f’(x)=0] og får x = −1 som svar. Det
neste vi vil gjøre er å finne punktet på grafen. Siden vi allerede har definert f(x) kan vi nå
skrive inn f(−1) og få at bunnpunktet er (−1, −1e).
88

11.3 Litt mer om input og output
Figur 71: Vi har funnet eksakte verdier med CAS.
Oppgave 60
Løs likningssystemet
2y − x 2 + 2x = a
y − 2x = 3
For hvilke verdier har systemet
– én løsning
– to løsninger
– ingen løsninger
Oppgave 61 Vi har en stige som er 10 meter lang. Denne skal plasseres opp mot en vegg.
Problemet er at inntil veggen står en kasse som er 1 meter høy og 1 meter bred og som vi ikke
kan ta vekk. Hva er det høyeste punktet over bakken at stigen kan nå på veggen Se figur 72.
10 m
x m
1 m
Figur 72: Stigeproblemet i oppgave 61
11.3 Litt mer om input og output
Når vi skal løse litt større oppgaver, slik som den i eksempel 39 er det viktig å få en god
arbeidsflyt. Vi har tidligere nevnt at det er unødvendig å skrive opp uttrykk manuelt dersom
vi allerede har regnet dem ut i CAS. Her er noen nyttige tips:
89

11.3 Litt mer om input og output
– Likhetstegn (=) vil skrive inn forrige input
– Mellomromstast vil skrive inn forrige output
– Høyreparentes ) vil skrive inn forrige output med parenteser rundt.
– Du kan referere til forrige output ved å skrive enten $ (for dynamisk output) eller
# (for statisk output). Tilsvarende kan du referere til output på rad n ved å skrive
$n (for dynamisk output) og #n (for dynamisk output. Forskjellen på disse to er
dersom du går inn og endrer på en verdi slik at output på rad n endres, så vil du også
få endring i raden du skrev $n i mens du vil beholde den gamle verdien fra rad n
dersom du skrev #n.
Eksempel 39
La f være en tredjegradsfunksjon som har tre nullpunkt a, b og c. La T være tangenten til f i
d = a + b . Hva kan du si om denne tangenten
2
Løsning:
Før vi går i gang med selve løsningen i CAS kan det være en ide å utforske problemet litt.
Vi kan for eksempel se på funksjonen f(x) = (x − 1)(x − 3)(x − 4). I dette tilfellet blir
d = 2 og vi kan tegne og finne tangenten ved å skrive inn kommandoen Tangent[2,f] i
inntastingsfeltet.
y
3
T
f
2
1
−1 0 1 2 3 4 5 6 7
x
Ut fra denne figuren får vi en mistanke om at tangenten vil gå gjennom det tredje nullpunktet.
Vi ønsker derfor å bevise dette ved å bruke et CAS!
Det første vi gjør er å definere funksjonen ved å skrive inn
90

11.3 Litt mer om input og output
f(x):=(x-a)(x-b)(x-c)
Vi kan finne tangenten i a+b
2 , f a+b
2
ved å bruke ettpunktsformelen. Til det trenger vi
f a+b
2 og stigningstallet f′ a+b .
2
Sistnevnte får vi ved å bruke verktøyet Sett inn. Ettpunktsrmelen
gir oss at tangenten har likningen
y = −a3 + a 2 (b + 2c) + a(b 2 − 4ac) − b 3 + 2b 2 c
8
+ −a2 + 2ab − b 2
4
x − a + b
2
På linje 5 på figur 73 har vi definert denne som en egen funksjon g(x). Merk hvordan vi
refererer til outputene $3 og $4 i definisjonen av g. Dette gir oss mulighet til finne g(c). Vi
ser at svaret blir 0 som forventet!
Figur 73: Tangenten til f i middelverdien til to av nullpunktene går alltid gjennom det tredje
nullpunktet!
Nå finnes det finnes en enklere måte å løse dette problemet på i GeoGebra. Vi kan rett og
slett bruke kommandoen Tangent[,] som vist på figur 74. Merk at
tangenten ikke er en funksjon, men en linje. For å kunne finne y-verdien til denne tangenten
når x = c bruker vi derfor verktøyet Bytt ut.
91

11.3 Litt mer om input og output
Figur 74: Tangent-kommandoen fungerer i CAS også!
For den interesserte leser kan vi også nevne en tredje løsning som like lett lar seg gjøre med
papir og blyant. Ved et eventuelt koordinatskifte kan vi anta at nullpunktene er x = ±1 og
x = c. Middelverdien mellom de to første nullpunktene er da 0.
Vi har altså at f(x) = (x 2 − 1)(x − c). Den deriverte er f ′ (x) = 2x(x − c) + (x 2 − 1). Videre
er f ′ (0) = −1 og f(0) = c. Ettpunktsformelen gir oss derfor at tangenten er grafen til
g(x) = c − (x − 0) = c − x
Vi ser da at g(c) = 0. Smart ikke sant!
Eksempel 40
La f være en tredjegradsfunksjon som har et topp- og et bunnpunkt. La l være linja som går
gjennom topp- og bunnpunktet og t være linja som tangerer grafen til f i punktet (m, f(m)
der m er gjennomsnittet av x-koordinatene til topp- og bunnpunktet.
Vis at forholdet mellom stigningstallene til l og t er 2 3
Løsning:
Vi vet at slike funksjoner generelt kan skrives som f(x) = k(x − a)(x − b)(x − c) + d. Uten
å miste generalitet kan vi anta at k = 1 og d = 0 (Hvorfor).
Vi definerer f(x):
Skriver inn f(x) og klikker deretter på verkøtøyet Derivert
for å finne f ′ (x):
92

11.3 Litt mer om input og output
Trykker på mellomromstasten og bruker verktøyet Løs
null:
for å finne når den deriverte er
Output er en liste på formen x = . . . , x = . . . . Vi ønsker å regne ut middelverdien til de to
uttrykkene på høyresiden av elementene i listen over. For å gjøre dette kan vi først lage en
liste som består av høyresiden til de to elementene i output på rad 3:
Det neste vi vil gjøre er å finne middelverdien til disse to tallene. Vi gjør dette ved å bruke
kommandoen Middelverdi:
Bruker kommandoen ByttUt for å bytte ut x med (a + b + c)3 (det vil si output på rad 5).
Vi finner da stigningstallet til tangenten t:
Regner ut stigningstallet til linja l gjennom topp-og bunnpunktet:
Til slutt regner vi ut forholdet mellom stigningstallene. Disse står nå som output i rad 6 og 7.
Skriver derfor inn $7/$6:
Vi ser at forholdet mellom stigningstallet til t og l alltid er 2 3 . 93

11.4 Oppgaver
11.4 Oppgaver
Oppgave 62
Bruk CAS til å forenkle uttrykkene:
a)
x 12 − 1
x 4 − x 2 + 1
b) (x + 1) 3 − x x + 1
Oppgave 63
Løs likningene
a) x 2 + 2x − 3 = 0
b) e 2x − e + 1 = 10
c) x + 18 + x + 3 − x + 14 − x + 5 = 0
Oppgave 64
Løs likningssystemet
x + y + 3 x + y = 18
x − y − 2 x − y = 15
Oppgave 65
Bruk CAS til å faktorisere polynomene:
a) P(x) = 2x 4 − 7x 3 + x 2 + 14x − 10
b) Q(x) = x 12 − 1
c) h(x) = x 5 + x 4 + x 3 + x 2 + x + 1
Følgende tre oppgaver er hentet fra utdanningsdirektoratets forslag til ny eksamensordning
for videregående skole.
Oppgave 66 (1T)
En funksjon f er gitt ved
f(x) =
2
x(x − 1) − 3x x + 1
x 2 − x
Skriv funksjonsuttrykket så enkelt spm mulig, og bestem eventuelle vertikale og horisontale
asymptoter for grafen til f.
Oppgave 67 (S2)
I denne oppgaven skal du finne mønstre og sammenhenger.
a) Det minste tallet som kan skrives som summen av to kubikktall på to måter er 1729:
1729 = 1 3 + n 3
1729 = m 3 + (m + 1) 3
Bestem n og m.
b) Det eneste kubikktallet som skrives som summen av tre påfølgende kubikktall, er 6 3 .
Bestem de tre kubikktallene ved å løse en likning.
94

11.4 Oppgaver
Oppgave 68 (R1)
12
y
S
x
Et rektangel er innskrevet i en sirkel med sentrum i S og med radius 12.
a) Forklar at arealet av rektangelet er gitt ved
A(x) = 4x 144 − x 2 ,
x ∈ 0, 12
b) Bestem det største arealet rektangelet har. Kommenter formen på rektangelet.
Oppgave 69 Fermatprimtall er primtall på formen F n = 2 2n + 1.
a) Vis at F n er primtall når n er 1, 2, 3 og 4.
b) Vis at F n ikke er primtall når n er 5, 6, 7, 8, 9 og 10.
I denne oppgaven kan du bruke kommandoen ErPrimtall[].
Oppgave 70 I denne oppgaven skal vi studere polynomet P(x) = x 2 − x + 41.
a) Undersøk om P(n) er primtall for n ∈ 1, 2, 3, . . . , 10.
b) Finn minste naturlige tall n slik at P(n) ikke er et primtall.
Oppgave 71 Finn likningen til vendetangenten til funksjonen f(x) = x 3 − ax + b.
95