Determinanti. Kramera formulas.

Mana personīgā lapa − šeit.
Adrese komentāriem: Karlis.Podnieks@lu.lv
Algebra:
Determinanti
Kārlis Podnieks, LU profesors
Lekcijas
This work is licensed under a Creative Commons License and is copyrighted © 2009-2014 by
me, Karlis Podnieks.
Literatūra
[1] E-kursa materiāli (latviešu valodā).
[2] A. G. Kurošs. Vispārīgās algebras kurss. Nauka, Maskava,
1971 (vai cita gada izdevums), piejama tiešsaistē šeit (krievu
valodā).
[3] Determinant Wikipedia − ātram pārskatam, ja tēma jau
zināma.
[4] WolframAlpha Wikipedia − aprēķiniem tiešsaistē.
2 vienādojumi ar 2 nezināmajiem
(otrās kārtas determinanti)
a 11
x 1
+a 12
x 2
=b 1 ;
a 21
x 1
+a 22
x 2
=b 2 .
Mēģināsim risināt vispārīgā veidā.
a) Pirmo vienādojumu reizinām ar a22, otro – ar a12 un atņemam otro no pirmā
(pazūd x2):
a 11 a 22 x 1 +a 12 a 22 x 2 =b 1 a 22
;
a 12 a 21 x 1 +a 12 a 22 x 2 =b 2 a 12
;
(a 11
a 22
−a 12
a 21
) x 1
=b 1
a 22
−b 2
a 12
b) Otro vienādojumu reizinām ar a11, pirmo –ar a21 un atņemam pirmo no otrā
(pazūd x1):
a 11 a 21 x 1 +a 12 a 21 x 2 =a 21 b 1
;
a 11 a 21 x 1 +a 11 a 22 x 2 =a 11 b 2
;
(a 11
a 22
−a 12
a 21
) x 2
=a 11
b 2
− a 21
b 1
Rezultātā esam ieguvuši, ka:
(a 11 a 22 − a 12 a 21 ) x 1 =b 1 a 22 − b 2 a 12 ;
(a 11 a 22 − a 12 a 21 ) x 2 =a 11 b 2 −a 21 b 1 .
Redzam, ka izteiksme
d=a 11
a 22
− a 12
a 21
nosaka pašu galveno: ja d≠0, tad sistēmai ir viens vienīgs
atrisinājums, bet ja d=0, tad atrisinājumu nav nemaz vai ir
bezgalīgi daudz.
Tāpēc skaitli
d=a 11 a 22 − a 12 a 21
ir pieņemts saukt par sistēmas determinantu
(“noteicēju”), un to ir ērti pierakstīt tā:
| a 11
a 12
a 21 a 22| =a 11 a 22 −a 12 a 21 .
(Izteiksmei ir 4 mainīgie, to ir ērti pierakstīt matricas formā – tā, kā tie parādās
vienādojumu sistēmas pierakstā.)
WolframAlpha sintakse: Det [{1,2}, {4,5}] = −3.
Teorēma. Ja (2x2 lineāru vienādojumu)
sistēmas determinants nav nulle, tad sistēmai ir
viens vienīgs atrisinājums, bet ja determinants
ir nulle, tad atrisinājumu nav nemaz vai ir
bezgalīgi daudz.
Kramera formulas (kārtula, likums)
Ja sistēmai ir viens atrisinājums, tad, izmantojot determinanta

simbolu, šo atrisinājumu var uzrakstīt ļoti eleganti (sk.
augstāk):
d 1
=b 1
a 22
−b 2
a 12
=∣
b 1
a 12
b 2
a 22∣
(šis determinants iegūts
no d, aizstājot pirmo kolonu ar brīvo locekļu vektoru);
d 2
=a 11
b 2
−a 21
b 1
=∣
a 11
b 1
a 21
b 2∣
(šis determinants iegūts
no d, aizstājot otro kolonu ar brīvo locekļu vektoru);
x 1 = d 1
d ; x 2= d 2
d .
Kramera kārtula. Ja 2x2 lineāru vienādojumu
sistēmas determinants nav nulle, tad sistēmai ir
viens vienīgs atrisinājums, un to var uzrakstīt
kā:
x 1 = d 1
d ; x 2= d 2
d ;
Tās sauc par Kramera formulām.
[Kārtula – rule, правило. Dažreiz saka “Kramera likums”, kas
nav gluži korekti.]
Gabriels Kramers (1704-1752) tās publicēja 1750.gadā (n
vienādojumiem ar n nezināmajiem).
Cramer' s rule Wikipedia , Gabriel Cramer Wikipedia
Kolins Maklorens () – Colin Maclaurin (1698-1746) šīs formulas esot zinājis
jau 1729.gadā, bet publikācija iznāca tikai 1748.gadā (jau pēc autora nāves).
Piemērs vienādojumu sistēmas risinājumam ar Kramera formulām:
2x+3y=5, 2x − 3y=1; d = 2*(−3) − 3*2 = −12; d 1
= 5*(−3) − 3*1 = −18; d 2
=
2*1−5*2 = −8; x = 3/2; y = 2/3.
a 11
x 1
=b 1
1 vienādojums, 1 nezināmais
(pirmās kārtas determinanti)
Arī šajā gadījumā varam runāt par determinantu un Kramera
formulām:
d= |a 11
| = a 11
;
d 1
= |b 1
| = b 1
;
x 1 = d 1
d .
1.kārtas determinanta apzīmējums sakrīt ar vispārpieņemto
skaitļa moduļa apzīmējumu. Cerēsim, ka sajukums
neveidosies...
Un pavisam viegli var pierādīt arī teorēmu:
Teorēma. Ja (1x1 lineāra) vienādojuma
a 11
x 1
=b 1
determinants |a 11
| nav nulle, tad
vienādojumam ir viens vienīgs atrisinājums, bet
ja determinants ir nulle, tad atrisinājumu nav
nemaz vai ir bezgalīgi daudz.
Kramera kārtula. Ja 1x1 lineāru vienādojumu
sistēmas determinants nav nulle, tad sistēmai ir
viens vienīgs atrisinājums, un to var uzrakstīt
kā:
x 1 = d 1
d .
3 vienādojumi, 3 nezināmie
(trešās kārtas determinants)
a 11
x 1
+a 12
x 2
+a 13
x 3
=b 1
;
a 21
x 1
+a 22
x 2
+a 23
x 3
=b 2
;

a 31
x 1
+a 32
x 2
+a 33
x 3
=b 3
.
Vai arī šai gadījumā sistēmas pamatīpašību varēsim reducēt uz
viena skaitļa (determinanta) aprēķināšanu T.i. aprēķinām kādu
izteiksmi, un tās vērtība pasaka vai sistēma ir noteikta vai nav
Risinot vispārīgā veidā, mēs redzētu, ka sanāk formulas:
(a 11 a 22 a 33 − a 11 a 23 a 32 +a 12 a 23 a 31 −a 12 a 21 a 33 +a 13 a 21 a 32 − a 13 a 22 a 31 ) x 1 =
= b 1 a 22 a 33 − b 1 a 23 a 32 +a 12 a 23 b 3 − a 12 b 2 a 33 +a 13 b 2 a 32 − a 13 a 22 b 3
(a 11 a 22 a 33 − a 11 a 23 a 32 +a 12 a 23 a 31 − a 12 a 21 a 33 +a 13 a 21 a 32 − a 13 a 22 a 31 ) x 2 = ...
(a 11 a 22 a 33 − a 11 a 23 a 32 +a 12 a 23 a 31 − a 12 a 21 a 33 +a 13 a 21 a 32 − a 13 a 22 a 31 ) x 3 = ...
Tātad:
d x 1
= d 1
;
d x 2
= d 2
;
d x 3
= d 3
,
kur visas 4 izteiksmes d, d 1
, d 2
, d 3
ir diezgan sarežģītas, sk. arī
http://estudijas.lu.lv/mod/resource/view.phpid=78648
(formula 2.8).
Un noteicēja (determinanta) lomu šeit spēlē arī diezgan
sarežģīta izteiksme d.
Analizējot d izteiksmi, varam konstatēt, ka
d=a 11| a 22
a 23
a 32 a 33| −a 12| a 21
a 23
a 31 a 33| +a 13| a 21
a 22
a 31 a 32| ,
jeb:
d=a 11 D 11 − a 12 D 12 +a 13 D 13 ,
(plus − mīnus − plus!)
kur D 1j
ir 2x2 determinants, ko iegūst no d,
izsvītrojot pirmo rindu un j-o kolonu.
Tātad mēs varētu ievest šādu trešās kārtas (3x3)
determinanta definīciju:
d=| a 11
a 12
a 13
a 21 a 22 a 23
a 31 a 32 a 33| =a 11 D 11 − a 12 D 12 +a 13 D 13 ,
kur D 1j
ir 2x2 determinants, ko iegūst no d,
izsvītrojot pirmo rindu un j-o kolonu.
WolframAlpha sintakse: Det [{1,2,3}, {4,5,6},{7,8,9}] = 0.
Pieņemot šādu 3x3 determinanta definīciju, var pierādīt
teorēmu, kas apliecina, ka tiešām esam ieguvuši “noteicēju”
3x3 vienādojumu sistēmām:
Teorēma. Ja 3x3 lineāru vienādojumu sistēmas
determinants nav nulle, tad sistēmai ir viens
vienīgs atrisinājums, bet ja determinants ir
nulle, tad atrisinājumu nav nemaz vai ir
bezgalīgi daudz.
Pierādījums seko no
http://estudijas.lu.lv/mod/resource/view.phpid=78648
redzamās izteiksmes (formula 2.8) un tās analogiem priekš x 2
un x 3
.
Analizējot garo formulu labās puses, redzam, ka
arī 3x3
=∣
sistēmām sanāk skaistas Kramera formulas:
b 1
a 12
a 13
d 1 b 2 a 22 a 23
(šis determinants iegūts no d,
b 3 a 32 a
aizstājot pirmo kolonu
33∣
ar brīvo locekļu vektoru);

=∣ a 11
b 1
a 13
d 2 a 21 b 2 a 23
a 31 b 3 a 33∣
(šis determinants iegūts no d,
aizstājot otro kolonu ar brīvo locekļu vektoru);
d 3 =∣
a 11
a 12
b 1
a 21 a 22 b 2
a 31 a 32 b 3∣
(šis
determinants iegūts no d,
aizstājot trešo kolonu ar brīvo locekļu vektoru).
Kramera kārtula. Ja 3x3 lineāru vienādojumu
sistēmas determinants nav nulle, tad sistēmai ir
viens vienīgs atrisinājums, un to var uzrakstīt
kā:
x 1 = d 1
d ; x 2= d 2
d ; x 3= d 3
d .
Piemērs.
x+2y+3z=1,
2x+2y+z=3,
3x+3y+5z=4;
d=| 1 2 3
5|
2 2 1 =
=∣
3 3 1 2 3
d 1 3 2 1
d 2 =∣
d 3 =|
5∣
=
4 3
5∣
=
3 4
4|
2 2 3 =
3 3
1 1 3
2 3 1
1 2 1
Det [{1,2,3}, {2,2,1},{3,3,5}] = −7.
Det [{1,2,3}, {3,2,1},{4,3,5}] = −12.
Det [{1,1,3}, {2,3,1},{3,4,5}] = 1.
Det [{1,2,1}, {2,2,3},{3,3,4}] = 1.
x= 12 7 ; y=− 1 7 ; z=− 1 7
, ko mēs jau zinām.
Vēlāk redzēsim, ka determinantu vērtību aprēķiniem visātrāk un ērtāk ir
izmantot... to pašu Gausa metodi.
Praktiskai vienādojumu sistēmu risināšanai Kramera
formulas nav piemērotas, jo vēlāk mēs redzēsim, ka viena
determinanta aprēķināšana prasa aptuveni tikpat daudz laika kā
visas vienādojumu sistēmas atrisināšana ar Gausa metodi. Bet
Kramera formulas 3x3 sistēmai taču satur 4 determinantus...
Kam tad determinanti vispār vajadzīgi To mēs pa īstam
sapratīsim, kad studēsim matricu teoriju.
Interesanti! Determinants kā tilpuma formula – sk. bildes no
Determinant Wikipedia .
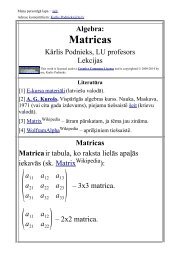
Matricas
Lai tālāk vispārinātu determinanta formulu (4x4, 5x5 utt.
gadījumiem), vispirms ievedīsim matricas jēdzienu − matrica
ir tabula, ko raksta lielās apaļajās iekavās (sk.
Matrix Wikipedia ):
(a 11 a 12 a 13
a 21
a 22
a 23
a 31
a 32
a 33)
− 3x3 matrica;
( a 11 a 12
a 21
a 22)
(a 11
) − 1x1 matrica;
− 2x2 matrica;
(a 11
a 12
) − 1x2 matrica (horizontāls vektors);

( a 11
a 21)
− 2x1 matrica (vertikāls vektors).
Jēdziens par s x n matricu − s rindiņas, n
kolonas: (a ij
| i=1..s; j=1..n):
(a 11 a 12 ... a 1n
a 21 a 22 ... a 2n
... ... ... ...
a s1
a s2
... a sn)
.
Skaitļus a ij
sauc par matricas elementiem (i ir rindas numurs, j
– kolonas numurs).
Elementi a ii
, t.i. a 11
, a 22
, a 33
, ... veido matricas diagonāli.
n x n matricu sauc par kvadrātisku matricu. Tās izmanto
visbiežāk.
Ja n x n matricai zem diagonāles visi elementi ir nulles, tad to
sauc par trīsstūra matricu. (Citiem vārdiem: ja i>j, tad a ij
= 0).
[Piemērs.]
s x n lineāras vienādojumu sistēmas
a 11
x 1
+a 12
x 2
+ ... + a 1n
x n
=b 1
;
a 21
x 1
+a 22
x 2
+ ... + a 2n
x n
=b 2
;
...
a s1
x 1
+a s2
x 2
+ ... + a sn
x n
=b s
koeficientu matrica A = (a ij
| i=1..s; j=1..n) un
brīvo locekļu (vertikālais) vektors
B = (b i
| i=1..s).
Piemērs.
x+2y+3z=1,
2x+2y+z=3,
3x+3y+5z=4.
Koeficientu matrica:
(
(a 11 a 12 ... a 1n
a 21 a 22 ... a 2n
... ... ... ...
a s1
a s2
... a sn)(x
1 2 3
2 2 1
3 3 5)
,
1
1
x 2 b 2
... ...
x n)=(b s)
.
b
brīvo locekļu vektors:
(
Kopskats:
1 3
4)
(vertikāls!).
(
1 2 3
5)( x z) ( 1 4)
2 2 1 y = 3 .
3 3
n x n matricas determinants
Kvadrātiskas matricas A determinantu apzīmē
ar |A| vai det(A).
Mēģināsim pēc analoģijas 3x3 matricām uzminēt n×n
matricas determinanta definīciju.
1x1 gadījumā:
det(A) = a 11
.
2x2 gadījumā:

det(A) = = a 11
a 22
− a 12
a 21
=
a 11
det(A 11
) − a 12
det(A 12
) .
A1j te ir matrica, kas iegūta no matricas A, izsvītrojot pirmo
rindu un j-to kolonu.
3x3 gadījumā:
det(A) =
a 11
det(A 11
) − a 12
det(A 12
) + a 13
det(A 13
).
A1j te ir matrica, kas iegūta no matricas A, izsvītrojot pirmo
rindu un j-to kolonu.
Tātad − mēģināsim minēt, ka
4x4 gadījumā:
det(A) =
a 11
det(A 11
) − a 12
det(A 12
) +
a 13
det(A 13
) − a 14
det(A 14
)
5x5 gadījumā: det(A) =
a 11
det(A 11
) − a 12
det(A 12
) +
a 13
det(A 13
) − a 14
det(A 14
) + a 15
det(A 15
)
Izskatās cerīgi...
n x n matricas determinanta definīcija
1) Ja n=1, tad:
det ( A)=a 11
.
2) Pieņemsim, ka (n−1)x(n−1) matricām A determinants det(A)
jau ir definēts.
Tad n x n matricai A = (a ij
| i=1..n; j=1..n) definējam det(A) pēc
analoģijas ar 3x3 gadījumu:
n
det ( A)=∑
j=1
(−1) 1+ j a 1j det ( A 1j ) ,
kur A 1j
ir (n−1)x(n−1) matrica, ko iegūst no A,
izsvītrojot no tās 1-o rindu un j-to kolonu.
[Ko nozīmē (−1) 1+j Tādā veidā mēs ģenerējam saskaitāmo
zīmes: + − + − ...]
Mūsu galamērķis
ir divas teorēmas, kas parādīs, ka mūsu "uzminētais"
determinanta jēdziens tiešām spēlē "noteicēja" lomu n x n
lineāru vienādojumu sistēmu risināšanā.
a 11
x 1
+a 12
x 2
+ ... + a 1n
x n
=b 1
;
a 21
x 1
+a 22
x 2
+ ... + a 2n
x n
=b 2
;
...
a n1
x 1
+a n2
x 2
+ ... + a nn
x n
=b n
.
Koeficientu matrica: A = (a ij
| i=1..n; j=1..n).
Brīvo locekļu vertikālais vektors:
B = (b i
| i=1..n).
Teorēma. Ja n x n lineāru vienādojumu sistēmas
koeficientu matricas A determinants det(A) nav
nulle, tad sistēmai ir viens vienīgs atrisinājums,
bet ja determinants ir nulle, tad atrisinājumu
nav nemaz vai ir bezgalīgi daudz.
Kramera kārtula. Ja n x n lineāru vienādojumu
sistēmas koeficientu matricas A determinants
det(A) nav nulle, tad sistēmai ir viens vienīgs
atrisinājums, ko var iegūt ar Kramera
formulām:

x i = det( A i)
det ( A) ; i=1..n,
kur A i
ir n x n matrica, ko iegūst no A, aizstājot
tās i-to kolonu ar sistēmas brīvo locekļu
vektoru B.
Pierādījums. Ja n=1, 2 vai 3, tad jau redzējām, ka abas šīs
teorēmas var pierādīt ar mazāku vai lielāku izteiksmju
pārveidojumiem. Sākot ar n=4 tāda metode vairs nav cilvēkam
pa spēkam. Tā vietā vispirms ir jāizpētī determinantu īpašības...
Datoriķiem
Praktiskai vienādojumu sistēmu risināšanai Kramera formulas
nav piemērotas, jo vēlāk mēs redzēsim, ka (pat izmantojot
vislabāko metodi) viena determinanta aprēķināšana prasa
aptuveni tikpat daudz laika kā visas vienādojumu sistēmas
atrisināšana ar Gausa metodi. Bet Kramera formulas
n x n sistēmai satur n+1 determinantu...
Kam tad determinanti vispār vajadzīgi To mēs pa īstam
sapratīsim, kad studēsim matricu teoriju.
Piemērs.
Kas ir matemātiskā indukcija
1=1 2 ;1+ 3=2 2 ;1+ 3+ 5=3 2 ;
1+ 3+ 5+ 7=4 2 ;1+ 3+ 5+ 7+ 9=5 2 ; utt.
Vispārinot, varam izteikt hipotēzi: pirmo n nepārskaitļu
summa ir n 2 .
Citiem vārdiem:
1+ 3+ 5+ ...+ (2n−1)=n 2 .
Jau pārliecinājāmies, ka šī formula izpildās pie n=1, 2, 3, 4, 5.
Bet kā pierādīt, ka tā izpildās jebkuram n
Matemātiskas indukcijas metode (1.versija):
1) Indukcijas bāze. Pierādām, ka formula izpildās pie n=1.
2) Indukcijas solis. Pieņemam, ka formula izpildās skaitlim n.
Un izvedam no šī pieņēmuma, ka tad formula izpildās arī
skaitlim n+1.
3) Secinām, ka formula izpildās visiem skaitļiem n.
Mūsu konkrētajai formulai:
1) Indukcijas bāze. Ja n=1, tad 1=1 2 , t.i. formula izpildās.
2) Indukcijas solis. Pieņemam, ka formula izpildās skaitlim n:
1+ 3+ 5+ ...+ (2n−1)=n 2 .
Skaitlim n+1:
1+ 3+ 5+ ...+ (2n−1)+ (2n+ 1)=n 2 + 2n+ 1=(n+ 1) 2 .
3) Secinām, ka formula izpildās visiem skaitļiem n.
Matemātiskas indukcijas metode (2.versija):
1) Indukcijas bāze. Pierādām, ka formula izpildās pie n=1.
2) Indukcijas solis. Pieņemam, ka formula izpildās visiem
skaitļiem, kas mazāki par n. Un izvedam no šī pieņēmuma, ka
tad formula izpildās arī skaitlim n.
3) Secinām, ka formula izpildās visiem skaitļiem n.
Determinantu īpašības
Lielāka daļa no šīm īpašībām ir kaut kādā ziņā kopīgas
determinantiem un lineāru vienādojumu sistēmām. Vēlāk
redzēsim, ka šīs īpašības ļauj determinantu rēķināšanai
izmantot to paša Gausa metodi, ko izmanto vienādojumu
sistēmu risināšanai.
1. Ja matricā kāda rinda sastāv tikai no
nullēm, tad tās determinanta vērtība ir 0.
Piemēri.

|
0
0
a 21 a 22| =0⋅a 22−0⋅a 21 =0 ;
| a 11 a 12
0 0
| =a 11⋅0−a 12
⋅0=0 ;
|
0 0 0
2 2 3
4| | 1 2 1
=0 ; 0 0 0
3 3
3 3 4| =0 ;
Pierādījums. Viegls: indukcija pa n (bāze un solis), atsevišķi
aplūkojot pirmo rindu un pārējās.
1'. Ja matricā kāda kolona sastāv tikai no
nullēm, tad tās determinanta vērtība ir 0.
Pierādījums. Viegls: indukcija pa n (bāze un solis).
2. Ja matricā zem diagonāles ir tikai nulles
(trīsstūra matrica), tad tās determinanta
vērtība ir visu diagonāles elementu reizinājums.
(Piemēram, 3x3 gadījumā: det(A) = a 11
a 22
a 33
).
Pierādījums. Viegls: seko no 1', indukcija pa n (bāze un solis).
3. Ja matricā divas rindas apmaina vietām, tad
tās determinanta vērtība mainās uz pretējo (ja
bija d, tad kļuva –d). [Piemērs.]
Pierādījums. Grūtāks – sk. e-kursa materiālus.
4. Ja matricā divas rindas ir vienādas, tad tās
determinanta vērtība ir 0. [Piemērs.]
Pierādījums. Viegls: uzreiz seko no 3.
5. Ja kādā matricas rindā visus skaitļus
pareizina ar skaitli c, tad arī maticas
determinanta vērtība pareizinās ar c. [Piemērs.]
Pierādījums. Viegls: indukcija pa n (bāze un solis), atsevišķi
aplūkojot pirmo rindu un pārējās.
6. Ja matricā kāda rinda ir iegūta no citas
rindas, reizinot ar kādu skaitli (t.i. divas
rindas ir proporcionālas), tad matricas
determinanta vērtība ir 0. [Piemērs.]
Pierādījums. Viegls: uzreiz seko no 4 un 5.
7. Ja matricas A i-jā rindā katrs elements ir divu
skaitļu summa a ij
=b j
+c j
, tad det(A)=det(B)
+det(C), kur matricas B un C ir iegūtas no A,
izstājot i-jā rindā katru a ij
attiecīgi ar b j
vai c j
.
[Piemērs.]
Pierādījums. Viegls: indukcija pa n (bāze un solis), atsevišķi
aplūkojot pirmo rindu un pārējās.
Kas ir lineāra kombinācija (a, b, c – skaitļi):
r i
= ar k
+br l
+cr m
.
8. Ja matricā kāda rinda ir citu rindu lineāra
kombinācija (piemēram, summa), tad tās
determinanta vērtība ir 0. [Piemērs ar rindu summu.]
Pierādījums. Viegls: uzreiz seko no 7 un 6.
9. Ja determinantā kādai rindai pieskaita vai

atņem citu rindu, pareizinātu ar kādu
skaitli, tad determinanta vērtība nemainās.
Pierādījums. Viegls: uzreiz seko no 7 un 6. [Piemērs.]
9'. Ja determinantā kādai rindai pieskaita citu
rindu lineāru kombināciju, tad determinanta
vērtība nemainās.
Pierādījums. Kā 9.
Vēlreiz: kā redzam, determinantu īpašības
atgādina vienādojumu sistēmu īpašības!
Transponētā matrica
Matricas A transponēto matricu A T iegūst,
pagriežot A ap diagonāli.
Citiem vārdiem: ja A=(a ij
| i, j=1..n), un A T =(b ij
| i, j=1..n), tad
b ij
= a ji
.
Piemērs.
(
1 2 3
4 5 6
7 8 9)T
=( 1 4 7
2 5 8
3 6 9)
.
10. det(A T ) = det(A), t.i. transponējot matricu,
tās determinants nemainās.
Pierādījums. Grūtāks − sk. e-kursa materiālus. [Piemērs: n=2.]
Kāpēc mums to vajadzēja
Secinājums. Visas īpašības 1.-9'. izpildās arī
determinantu kolonām.
Tagad mēs tiešām varētu pierādīt arī abas minētās teorēmas par
n x n lineāro vienādojumu sistēmu risināšanu, izmantojot
determinantus.
Pierādījumi. Teorēmai – viegls: risinām sistēmu ar Gausa
metodi un sekojam determinanta vērtībai. Beigās iznāk
trīsstūris vai trapece. Kramera kārtulai – grūtāks, sk. e-kursa
materiālus.
Līdz ar to esam konstatējuši, ka mūsu
"uzminētā" n x n matricas determinanta
definīcija iecerēto mērķi ir sasniegusi: esam
atraduši tādu izteiksmi no n x n vienādojumu sistēmas
koeficientiem, kuras vērtība nosaka ("determinē") sistēmas
galveno īpašību − būt noteiktai vai nē.
Cik daudz laika aizņem determinanta
aprēķināšana
Jautājums datoriķiem − matemātikas cienītājiem: cik daudz
operāciju ir jāizpilda, lai aprēķinātu n x n matricas
determinanta vērtību
Ja, bez kādām viltībām, rēķināšanai izmantosim determinanta
definīciju, tad izrādās, ka mums vajadzēs ļoti daudz
reizināšanas, saskaitīšanas un atņemšanas operāciju.
Apzīmēsim šo operāciju skaitu n x n determinantam ar S(n).
n x n matricai A:
det(A) =a 11
det(A 11
)−a 12
det(A 12
)+a 13
det(A 13
)−a 14
det(A 14
)+...,
kur A 1j
visas ir (n−1)x(n−1) matricas.
Tātad:
S(n) =
n reizināšanas + n−1 saskaitīšanas un atņemšanas + n*S(n−1).
Protams, S(1)=0.
S(n) = n(2+S(n−1))−1.
Secinājumi: S(2) = 3; S(3) = 14; S(4)=63; S(5)=324;

S(6)=1955; ...
Uzdevums. Parādiet, ka S(n)>n! (n faktoriāls).
Secinājums: ja n>3, tad determinanta
definīcija ir praktiski nelietojama kā metode
n×n matricas determinanta vērtības
aprēķināšanai.
Determinantu aprēķināšana ar Gausa
metodi
Tāpēc pamēģināsim citu metodi.
Determinantu īpašība 2, īpašība 3 (rindām un kolonām), 5
(rindām) un 9 (rindām) liecina, ka determinantiem var lietot tās
pašas Gausa metodes operācijas a), b), c), d), ko lietojām
lineāru vienādojumu sistēmām.
Teorēma. Ar Gausa metodes operāciju a), b),
c), d) palīdzību jebkuru determinantu D var
pārveidot trīsstūra formā D', kurā uz diagonāles
ir tikai skaitļi 1 un 0. Tātad D'=0 vai D'=1.
Šajā procesā: operācija a) izdala determinanta
vērtību ar kādu nenulles skaitli c, operācija b)
determinanta vērtību nemaina, bet operācijas
c), d) maina determinanta zīmi uz pretējo.
Izpildot visas šīs operācijas apgrieztā secībā,
no D' vērtības (0 vai 1) iegūstam D vērtību.
Šis aprēķinu process beidzas ar trīsstūra matricu, kuras
determinants D' = 1 vai 0 (sk. īpašību 2). Ja operācijas c), d)
tika izmantotas t reizes, tad D' jāpareizina ar (−1) t . Un beidzot,
D' ir jāpareizina ar visiem skaitļiem c, ar kuriem dalījām
operācijās a).
[Piemērs. Det [{1,2,3}, {2,2,0},{3,3,2}] = −4.]
D=∣ 1 2 3
2∣ ∣ 1 2 3
2 2 0 ; (2)-2*(1); (3)-3*(1); D= 0 −2 −6
3 3 0 −3 −7∣ ; (2)/-2;
D
∣ 1 2 3
−2 = 0 1 3
0 −3 −7∣ ; (3)+3*(2); D
∣ 1 2 3
2∣ −2 = 0 1 3 ; (3)/2;
0 0
D
∣ 1 2 3
1∣ (−2)∗2 = 0 1 3 =1 ; tātad D=−4 .]
0 0
Par n x n determinanta rēķināšanas laiku ar Gausa metodi:
tāpat kā n x n vienādojumu sistēmai, vajadzīgas aptuveni 3n 3
operācijas. Salīdzinot ar n!, tas ir ļoti labs rādītājs!
Tātad Gausa metode ir efektīvs veids
determinanta vērtības aprēķināšanai.
Uzlabotā Gausa metode datoram
Grāmatās Jūs redzēsiet mazliet savādāku Gausa metodes
lietojumu determinantiem, kas ļauj ietaupīt daļu no operācijām:
− operāciju a) neizmantojam vispār, pieļaujot, ka determinanta
diagonāles elementi ne vienmēr ir vienādi ar 1;
− operācijā b), kuras mērķis ir ar j-tās rindas atņemšanu no i-tās
panākt, lai determinanta elements a ij
kļūtu vienāds ar nulli:
atņemam no i-tās rindas j-to rindu, pareizinātu ar
a ij
a jj
;
− operācijās c), d), mainot vietām divas rindas vai kolonas,
vienu no tām pareizinām ar −1.
Tādā veidā mēs katrā operācijā iegūstam determinantu, kura
vērtība ir vienāda ar sākotnējā determinanta vērtību.
[Pārliecinieties par to paši.]
Beigās tiek iegūta trīsstūra matrica, kuras determinants ir
diagonāles elementu reizinājums.
[Piemērs. Ar uzlaboto metodi: Det [{1,2,3}, {2,2,0},{3,3,2}] = −4.]
Par Gausa metodi determinantu aprēķinam
parasti sauc tieši šo uzlaboto metodi. Šī metode
ir ērtāka datoram (t.i. programmētājam), bet ne
cilvēkam, kurš aprēķinus veic uz papīra.

Laplasa teorēma
Pierre Simon Laplace Wikipedia (1749-1827)
Pa īstam ir vērts zināt tikai šīs teorēmas speciālgadījumu (k=1
attiecīgajā e-kursa materiālu nodaļā
http://estudijas.lu.lv/mod/resource/view.phpid=78651 − tur arī
sk. vispārīgo gadījumu.)
Būtībā Laplasa teorēma ir determinanta definīcijas
vispārinājums: ja savā sākotnējā definīcijā mēs speciāli
izdalījām determinanta pirmo rindu, tad tagad tās vietā
atļaujam izmantot jebkuru rindu vai kolonu. Iegūtā
determinanta vērtība no tā nemainās − to tad arī apgalvo
Laplasa teorēma.
Lai to precīzi pateiktu, ir jāieved jauns termins:
Par matricas A elementa a ij
algebrisko
papildinājumu (cofactor) sauksim skaitli
C ij =(−1) i+ j det( A ij ) ,
kur A ij
ir (n−1)x(n−1) matrica, ko iegūst no
matricas A, izsvītrojot i-to rindu un j-to kolonu.
[Piemērs: C 22
.]
Šajos terminos determinanta definīcija izskatās šādi:
n
det ( A)=∑
j=1
a 1j C 1j
.
Definējot n-tās kārtas determinanta vērtību, mēs izmantojām
matricas pirmo rindu, reizinot tās elementus ar to
algebriskajiem papildinājumiem, un reizinājumus summējot.
Izrādās, ka pirmās rindas vietā mēs varējām ņemt jebkuru rindu
vai jebkuru kolonu − rezultāts būs tas pats:
Laplasa teorēma. Ja ņemsim n×n matricas A
jebkuru rindu vai jebkuru kolonu un
sasummēsim visu tās elementu reizinājumus ar
to algebriskajiem papildinājumiem, tad iegūsim
det(A).
Pierādījums. Grūtāks, sk.
http://estudijas.lu.lv/mod/resource/view.phpid=78651.
Izmantojot Laplasa teorēmu, var samazināt aprēķinu apjomu,
rēķinot determinantus, kuri satur nulles.
Piemērs. Det [{1,2,3}, {2,2,0},{3,3,0}] = 12.
D=∣ 1 2 3
0∣
2 2 0
3 5
Šo deteminantu visērtāk aprēķināt, izmantojot trešo kolonu, jo tajā divi elementi
ir 0: saskaņā ar Laplasa teorēmu, D = 3∙C 13
+0∙C 23
+0∙C 33
, t.i. C 23
un C 33
nemaz nav jārēķina!
D=∣ 1 2 3
2 2 0
3 5 0∣ =3(−1)1+ 3 ∣ 2 2
3 5∣ + 0⋅C 23 + 0⋅C 33 =3⋅4=12 .