Galīgo elementu metode
Galīgo elementu metode Galīgo elementu metode
48 NODAĻA 3. SIJAS Q 2 Q 1 Q 3 Q 4 Q 5 Q 6 Q 7 Q 8 Q 9 Q 10 ! ! " " # q 1 q 3 q 2 q 4 e v 1v v ′ 2v ′ 1 2 Zīmējums 3.4: Sijas sadalīšana galīgos elementos Tabula 3.1: Sijas galīgo elementu savienojumu matrica Elements Mezgli Numerācija e 1 2 Lokālie numuri 1 1 2 Globālie numuri 2 2 3 Globālie numuri 3 3 4 Globālie numuri 4 4 5 Globālie numuri Visas sijas galīgo elementu savienojumu matrica ir attēlota Tabulā 3.2. Šo matricu izveido tāpat kā matricu stienim (sk. Tabulu 2.6). Elementa formas funkcijas, lai approksimētu izlieci v un nodrošinātu pārvietojumu nepārtrauktību, izvēlas Ermita polinomu veidā (sk. Zīm. 3.5). Tāpat kā iepriekš approksimācijai lieto elementa lokālo koordinātu sistēmu [−1 ≤ ξ ≤ +1] (sk. Zīm. 2.7). Sijas elementa formas funkcija atšķiras to stieņa elementa formas funkcijas. Tas ir tāpēc, ka sijas GE mezglu pārvietojumi ir izliece un tās atvasinājums (pagrieziena leņķis). Tieši Ermita formas funkcijas nodrošina gan izlieces, gan pagrieziena leņķa nepārtrauktību starp elementiem. Formas funkcija ir kubiskais polinoms H i = a i + b i ξ + c i ξ 2 + d i ξ 3 , i =1, 2, 3, 4 (3.11) Lai nodrošinātu galveno robežnoteikumu izpildi GE savienojumu vietās - mezglu punktos, formas funcijām ir jānodrošina noteikumi, kas parādīti Tabulā 3.2.
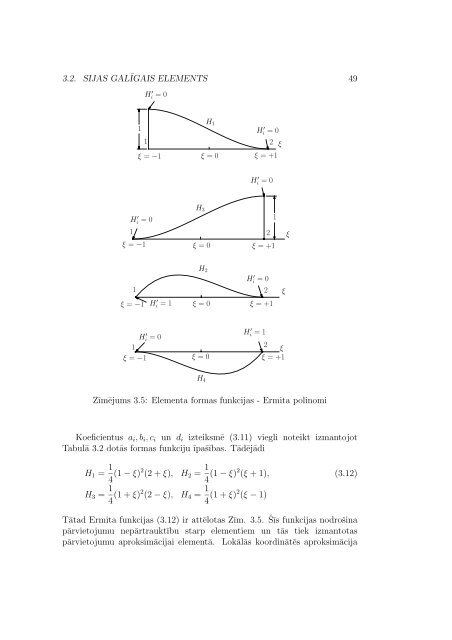
3.2. SIJAS GALĪGAIS ELEMENTS 49 H ′ i =0 1 1 ξ = −1 H 1 ξ =0 H i ′ =0 2 ξ ξ =+1 H i ′ =0 1 H i ′ =0 H 3 1 2 ξ = −1 ξ =0 ξ =+1 ξ H 2 H i ′ =0 H i ′ =1 1 2 ξ H i ′ =0 1 2 ξ ξ = −1 H i ′ =1 ξ =0 ξ =+1 H 4 ξ = −1 ξ =0 ξ =+1 Zīmējums 3.5: Elementa formas funkcijas - Ermita polinomi Koeficientus a i ,b i ,c i un d i izteiksmē (3.11) viegli noteikt izmantojot Tabulā 3.2dotās formas funkciju īpašības. Tādējādi H 1 = 1 4 (1 − ξ)2 (2 + ξ), H 2 = 1 4 (1 − ξ)2 (ξ +1), (3.12) H 3 = 1 4 (1 + ξ)2 (2 − ξ), H 4 = 1 4 (1 + ξ)2 (ξ − 1) TātadErmita funkcijas (3.12) ir attēlotas Zīm. 3.5. Šīs funkcijas nodrošina pārvietojumu nepārtrauktību starp elementiem un tās tiek izmantotas pārvietojumu aproksimācijai elementā. Lokālās koordinātēs aproksimācija
- Page 1: GALĪGO ELEMENTU METODE Rolands Rik
- Page 4 and 5: 4 zinātniskās monogrāfijās un r
- Page 6 and 7: 6 SATURS 4 Divdimensiju problēmas
- Page 8 and 9: 8 SATURS
- Page 10 and 11: 10 NODAĻA 1. TEORĒTISKAIS PAMATS
- Page 12 and 13: 12 NODAĻA 1. TEORĒTISKAIS PAMATS
- Page 14 and 15: 14 NODAĻA 1. TEORĒTISKAIS PAMATS
- Page 16 and 17: 16 NODAĻA 1. TEORĒTISKAIS PAMATS
- Page 18 and 19: 18 NODAĻA 1. TEORĒTISKAIS PAMATS
- Page 20 and 21: 20 NODAĻA 2. VIENDIMENSIJU PROBLĒ
- Page 22 and 23: 22 NODAĻA 2. VIENDIMENSIJU PROBLĒ
- Page 24 and 25: 24 NODAĻA 2. VIENDIMENSIJU PROBLĒ
- Page 26 and 27: 26 NODAĻA 2. VIENDIMENSIJU PROBLĒ
- Page 28 and 29: 28 NODAĻA 2. VIENDIMENSIJU PROBLĒ
- Page 30 and 31: 30 NODAĻA 2. VIENDIMENSIJU PROBLĒ
- Page 32 and 33: 32 NODAĻA 2. VIENDIMENSIJU PROBLĒ
- Page 34 and 35: 34 NODAĻA 2. VIENDIMENSIJU PROBLĒ
- Page 36 and 37: 36 NODAĻA 2. VIENDIMENSIJU PROBLĒ
- Page 38 and 39: 38 NODAĻA 2. VIENDIMENSIJU PROBLĒ
- Page 40 and 41: 40 NODAĻA 2. VIENDIMENSIJU PROBLĒ
- Page 42 and 43: 42 NODAĻA 2. VIENDIMENSIJU PROBLĒ
- Page 44 and 45: 44 NODAĻA 2. VIENDIMENSIJU PROBLĒ
- Page 46 and 47: 46 NODAĻA 3. SIJAS y p P m M k x L
- Page 50 and 51: 50 NODAĻA 3. SIJAS Tabula 3.2: Sij
- Page 52 and 53: 52 NODAĻA 3. SIJAS Ievērojot form
- Page 54 and 55: 54 NODAĻA 3. SIJAS 12 kN/m ! 1m
- Page 56 and 57: 56 NODAĻA 3. SIJAS v, mm M, kNm 10
- Page 58 and 59: 58 NODAĻA 4. DIVDIMENSIJU PROBLĒM
- Page 60 and 61: 60 NODAĻA 4. DIVDIMENSIJU PROBLĒM
- Page 62 and 63: 62 NODAĻA 4. DIVDIMENSIJU PROBLĒM
- Page 64 and 65: 64 NODAĻA 4. DIVDIMENSIJU PROBLĒM
- Page 66 and 67: 66 NODAĻA 4. DIVDIMENSIJU PROBLĒM
- Page 68 and 69: 68 NODAĻA 4. DIVDIMENSIJU PROBLĒM
- Page 70 and 71: 70 NODAĻA 4. DIVDIMENSIJU PROBLĒM
- Page 72 and 73: 72 NODAĻA 4. DIVDIMENSIJU PROBLĒM
- Page 74 and 75: 74 NODAĻA 5. SPIESTA STIEŅA NOTUR
- Page 76 and 77: 76 NODAĻA 5. SPIESTA STIEŅA NOTUR
- Page 78 and 79: 78 NODAĻA 5. SPIESTA STIEŅA NOTUR
- Page 80 and 81: 80 NODAĻA 6. DINAMIKAS UZDEVUMI Š
- Page 82 and 83: 82 NODAĻA 6. DINAMIKAS UZDEVUMI z
- Page 84 and 85: 84 NODAĻA 6. DINAMIKAS UZDEVUMI dV
- Page 86 and 87: 86 NODAĻA 6. DINAMIKAS UZDEVUMI 6.
- Page 88 and 89: 88 NODAĻA 6. DINAMIKAS UZDEVUMI at
- Page 90 and 91: 90 NODAĻA 7. KOPNES UN RĀMJI Q 2i
- Page 92 and 93: 92 NODAĻA 7. KOPNES UN RĀMJI (x 2
- Page 94 and 95: 94 NODAĻA 7. KOPNES UN RĀMJI q
- Page 96 and 97: 96 NODAĻA 7. KOPNES UN RĀMJI un f
3.2. SIJAS GALĪGAIS ELEMENTS 49<br />
H ′ i =0<br />
1<br />
1<br />
ξ = −1<br />
H 1<br />
ξ =0<br />
H i ′ =0<br />
2 ξ<br />
ξ =+1<br />
H i ′ =0 1<br />
H i ′ =0<br />
H 3<br />
1<br />
2<br />
ξ = −1<br />
ξ =0<br />
ξ =+1<br />
ξ<br />
H 2<br />
H i ′ =0 H i ′ =1<br />
1<br />
2<br />
ξ<br />
H i ′ =0<br />
1<br />
2 ξ<br />
ξ = −1 H i ′ =1 ξ =0<br />
ξ =+1<br />
H 4<br />
ξ = −1<br />
ξ =0<br />
ξ =+1<br />
Zīmējums 3.5: Elementa formas funkcijas - Ermita polinomi<br />
Koeficientus a i ,b i ,c i un d i izteiksmē (3.11) viegli noteikt izmantojot<br />
Tabulā 3.2dotās formas funkciju īpašības. Tādējādi<br />
H 1 = 1 4 (1 − ξ)2 (2 + ξ), H 2 = 1 4 (1 − ξ)2 (ξ +1), (3.12)<br />
H 3 = 1 4 (1 + ξ)2 (2 − ξ), H 4 = 1 4 (1 + ξ)2 (ξ − 1)<br />
TātadErmita funkcijas (3.12) ir attēlotas Zīm. 3.5. Šīs funkcijas nodrošina<br />
pārvietojumu nepārtrauktību starp elementiem un tās tiek izmantotas<br />
pārvietojumu aproksimācijai elementā. Lokālās koordinātēs aproksimācija