4 analisi del sistema di misura (msa) - Teletu
4 analisi del sistema di misura (msa) - Teletu 4 analisi del sistema di misura (msa) - Teletu
si tratta di un sistema per aggirare il problema semplicemente aumentando l'intervallo di riferimento e quindi la probabilità associata, ma deve coesistere una efficace opera di riduzione della variabilità . Con questo approccio la probabilità di ricadere al di fuori dei limiti è pari a cioè 2ppm. 1−Pr {−6 x6}=0.000002 5.5 dnorm(x) 0.0 0.1 0.2 0.3 0.4 -4 -2 0 2 4 x Figura 29: Distribuzione normale, limiti di tolleranza naturale Prima di proseguire nel cammino che porta alla costruzione degli indici di capacità, è importante valutare se la distribuzione della caratteristica oggetto di studio sia pressoché, se non proprio esattamente, normale. Un primo approccio potrebbe passare attraverso la costruzione dell'istogramma, oppure mediante il grafico quantile-quantile, ma esistono anche diverse tipologie di test sulla normalità come il Shapiro – Wilk test e il Jarque – Bera test. Il primo viene indicato come tra i più potenti test sulla normalità di una distribuzione, soprattutto se condotto su campioni di dimensione contenuta; esso prevede il raffronto tra uno stimatore non parametrico della varianza basato su di una combinazione lineare ottimale di una statistica d'ordine normale e la varianza campionaria. Ne scaturisce una statistica test W che può trovare spiegazione nel quadrato dell'indice di correlazione ( 2 ) in un grafico quantile-quantile. L'ipotesi nulla è quella di normalità, verrà quindi assunta la normalità della distribuzione per valori di p-value superiori ad un certo livello di significatività . Il secondo test nominato si basa sulla valutazione dei coefficienti di asimmetria e curtosi di una distribuzione, e considera come ipotesi nulla quella di normalità. Esiste un ulteriore test che appartiene alla categoria dei “non-parametrici”, dovuto a Kolmogorov e Smirnoff. La particolarità di questo test è quella di prescindere dalla distribuzione dei dati in oggetto e di confrontare la funzione di ripartizione empirica con quella teorica, basandosi sulla massima distanza che intercorre tra le due curve. Nasce come test di confronto dell'uguaglianza tra due distribuzioni, ma può essere applicato efficacemente per determinare la normalità di una distribuzione se il confronto avviene con la funzione di ripartizione teorica di una distribuzione gaussiana. In fase di valutazione dell'esito di un test è importante tener conto della numerosità 52
campionaria, in quanto di impatto sulla potenza del test stesso. Si ricorda che la funzione di potenza di un test è la probabilità di rifiutare l'ipotesi nulla H 0 (cioè la probabilità di ricadere nella regione di rigetto) per ogni valore del parametro . Rappresenta quindi la probabilità 1− di non commettere errore di II tipo (accettare un'ipotesi nulla falsa). 5.3 Indici di capacità Gli indici di capacità sono degli indicatori che traducono in valore numerico la capacità di un processo produttivo. Il primo indice che si incontra è l'indice C p , definito nel seguente modo USL− LSL C p = 6 5.6 in cui USL (Upper Specific Limit) è il limite si specifica superiore, mentre LSL (Lower Specific Limit) è quello inferiore. La quantità rappresenta lo standard error del processo, nel caso in cui non sia noto verrà stimato attraverso la deviazione standard campionaria S o con l'impiego del range medio diviso per la quantità d 2 . In tale circostanza anche l'indice C p risulterà essere una stima. Cerchiamo ora di valutare quale sia un buon valore per l'indice appena calcolato: in ambito produttivo, si vuole che l'intervallo in cui opera il processo, sia di dimensione inferiore alla dimensione dell'intervallo di specifica, determinando in questo modo valori superiori all'unità, con la preferenza per valori crescenti. Al contrario, valori inferiori all'unità ci informano che il processo impiega un'ampiezza superiore all'intero campo di specifica. Si vedano i grafici in Fig. 30, per una immediata comprensione. L'inverso dell'indice C p , espresso in valore percentuale, rappresenta l'ampiezza relativa di banda di specifica impiegata dal processo. P=100 1 C p 5.7 Più questa percentuale è bassa e più il processo lavora bene. L'indice C p sappiamo essere un indice che dà informazioni sull'ampiezza dei limiti di tolleranza naturale rispetto a quelli di specifica, ma nulla ci dice sulla posizione che il processo occupa rispetto alle specifiche; mi spiego meglio: il processo potrebbe sì operare con una contenuta variabilità, ma non essere centrato sul target. In questa situazione, potrebbero comunque prodursi molti più pezzi difettosi di quelli che ci si attenderebbe con una variabilità esigua. Per superare problemi di questo tipo, è stato creato un ulteriore indice che tiene conto della centratura del processo, denominato C pk e definito dalla formula 5.8. C pk =min C U ,C L 5.8 Dove C U e C L sono le capacità del processo in caso di specifiche unilaterali e così calcolati C U = USL− 3 − LSL C L = 3 5.9 5.10 53
- Page 1 and 2: UNIVERSITÀ CA’ FOSCARI DI VENEZI
- Page 3 and 4: Indice generale 1 INTRODUZIONE.....
- Page 5 and 6: inversamente proporzionale alla lor
- Page 7 and 8: cause che possono averlo determinat
- Page 9 and 10: 3 RACCOLA DATI L'attività di racco
- Page 11 and 12: Viene spesso indicata come equipmen
- Page 13 and 14: fatto che i punti cadano al di fuor
- Page 15 and 16: PV.perc=100 PV TV 4.19 La tabella s
- Page 17 and 18: Varianza dovuta all'interazione tra
- Page 19 and 20: 4.4 Applicazione 4.4.1 Il prodotto
- Page 21 and 22: Sinistro, punto A I dati sotto ripo
- Page 23 and 24: R chart Ranges 0.00 0.10 0.20 Op A
- Page 25 and 26: DF SS MS F value Pr(>F) Appraiser 1
- Page 27 and 28: R chart Ranges 0.00 0.06 0.12 Op A
- Page 29 and 30: Sinistro, punto C P1 P2 P3 P4 P5 P6
- Page 31 and 32: R chart Ranges 0.00 0.06 0.12 Op A
- Page 33 and 34: Il notevole grado di sovrapposizion
- Page 35 and 36: Ne risulta che l'indice GRR comples
- Page 37 and 38: Operatore A Operatore B -2.0 -1.5 -
- Page 39 and 40: Operatore A Operatore B -1.3 -1.2 -
- Page 41 and 42: Destro, punto C P1 P2 P3 P4 P5 P6 P
- Page 43 and 44: A fronte di quanto in precedenza af
- Page 45 and 46: R chart Ranges 0.00 0.04 0.08 Op A
- Page 47 and 48: Variance Std Deviation %TV %Contrib
- Page 49 and 50: Dopo le modifiche EV AV GRR PV TV V
- Page 51: 5 ANALISI DI CAPACITÀ 5.1 Introduz
- Page 55 and 56: Cpk=Cp dnorm(x) 0.0 0.2 0.4 USL LSL
- Page 57 and 58: questo caso, appare comunque suffic
- Page 59 and 60: Si può notare come il processo che
- Page 61 and 62: Process Capability Analysis Call: p
- Page 63 and 64: Capability indices: Value 2.5% 97.5
- Page 65 and 66: I risultati del test di Shapiro - W
- Page 67 and 68: 6 CARTE DI CONTROLLO 6.1 Fondamenti
- Page 69 and 70: R chart Quota 03 SX Moving Range 0.
- Page 71 and 72: Tutte queste indicazioni sono di im
- Page 73 and 74: Appendice A Data: Analisi del siste
- Page 75 and 76: grr.study
- Page 77 and 78: ##Calcolo SSE ss.e
- Page 79 and 80: } lines(m.b,type="b",pch=2,lty=1,co
- Page 81 and 82: Bibliografia D.C. Montgomery (200
si tratta <strong>di</strong> un <strong>sistema</strong> per aggirare il problema semplicemente aumentando l'intervallo <strong>di</strong> riferimento<br />
e quin<strong>di</strong> la probabilità associata, ma deve coesistere una efficace opera <strong>di</strong> riduzione <strong>del</strong>la variabilità<br />
.<br />
Con questo approccio la probabilità <strong>di</strong> ricadere al <strong>di</strong> fuori dei limiti è pari a<br />
cioè 2ppm.<br />
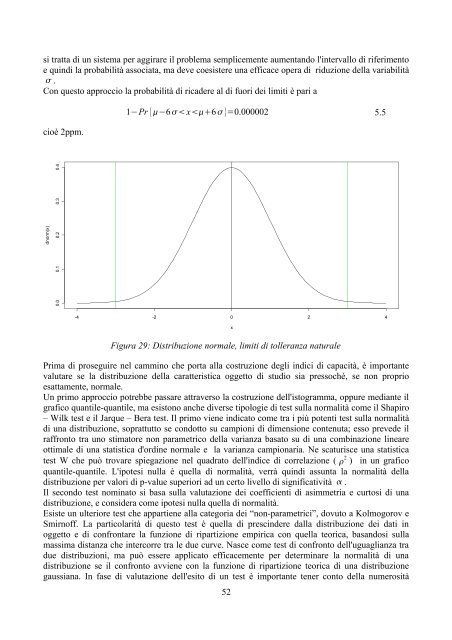
1−Pr {−6 x6}=0.000002 5.5<br />
dnorm(x)<br />
0.0 0.1 0.2 0.3 0.4<br />
-4 -2 0 2 4<br />
x<br />
Figura 29: Distribuzione normale, limiti <strong>di</strong> tolleranza naturale<br />
Prima <strong>di</strong> proseguire nel cammino che porta alla costruzione degli in<strong>di</strong>ci <strong>di</strong> capacità, è importante<br />
valutare se la <strong>di</strong>stribuzione <strong>del</strong>la caratteristica oggetto <strong>di</strong> stu<strong>di</strong>o sia pressoché, se non proprio<br />
esattamente, normale.<br />
Un primo approccio potrebbe passare attraverso la costruzione <strong>del</strong>l'istogramma, oppure me<strong>di</strong>ante il<br />
grafico quantile-quantile, ma esistono anche <strong>di</strong>verse tipologie <strong>di</strong> test sulla normalità come il Shapiro<br />
– Wilk test e il Jarque – Bera test. Il primo viene in<strong>di</strong>cato come tra i più potenti test sulla normalità<br />
<strong>di</strong> una <strong>di</strong>stribuzione, soprattutto se condotto su campioni <strong>di</strong> <strong>di</strong>mensione contenuta; esso prevede il<br />
raffronto tra uno stimatore non parametrico <strong>del</strong>la varianza basato su <strong>di</strong> una combinazione lineare<br />
ottimale <strong>di</strong> una statistica d'or<strong>di</strong>ne normale e la varianza campionaria. Ne scaturisce una statistica<br />
test W che può trovare spiegazione nel quadrato <strong>del</strong>l'in<strong>di</strong>ce <strong>di</strong> correlazione ( 2 ) in un grafico<br />
quantile-quantile. L'ipotesi nulla è quella <strong>di</strong> normalità, verrà quin<strong>di</strong> assunta la normalità <strong>del</strong>la<br />
<strong>di</strong>stribuzione per valori <strong>di</strong> p-value superiori ad un certo livello <strong>di</strong> significatività .<br />
Il secondo test nominato si basa sulla valutazione dei coefficienti <strong>di</strong> asimmetria e curtosi <strong>di</strong> una<br />
<strong>di</strong>stribuzione, e considera come ipotesi nulla quella <strong>di</strong> normalità.<br />
Esiste un ulteriore test che appartiene alla categoria dei “non-parametrici”, dovuto a Kolmogorov e<br />
Smirnoff. La particolarità <strong>di</strong> questo test è quella <strong>di</strong> prescindere dalla <strong>di</strong>stribuzione dei dati in<br />
oggetto e <strong>di</strong> confrontare la funzione <strong>di</strong> ripartizione empirica con quella teorica, basandosi sulla<br />
massima <strong>di</strong>stanza che intercorre tra le due curve. Nasce come test <strong>di</strong> confronto <strong>del</strong>l'uguaglianza tra<br />
due <strong>di</strong>stribuzioni, ma può essere applicato efficacemente per determinare la normalità <strong>di</strong> una<br />
<strong>di</strong>stribuzione se il confronto avviene con la funzione <strong>di</strong> ripartizione teorica <strong>di</strong> una <strong>di</strong>stribuzione<br />
gaussiana. In fase <strong>di</strong> valutazione <strong>del</strong>l'esito <strong>di</strong> un test è importante tener conto <strong>del</strong>la numerosità<br />
52