2. Cinematica Moto rettilineo - Definizioni elementari Definito un ...

2. Cinematica
Moto rettilineo - Definizioni elementari
Definito un asse di riferimento “x” per la descrizione del moto di un punto (per il momento
non si considera la sua massa), si definiscono:
- Legge oraria: x(t) (cioè la funzione che associa ad ogni istante “t” (secondi) una certa
posizione “x” (metri))
- Velocità media (m/s): v = x
t = x(t2) x(t1) , definita dallo spostamento x
t 2 t 1
nell’intervallo di tempo t 2 t 1 . NOTA: si osservi la distinzione tra posizione x e
spostamento x (variazione di posizione). In generale il simbolo si usa proprio per
indicare variazioni, cioè una data quantità a un certo istante meno la stessa quantità in un
istante precedente).
x(t + t) x(t)
- Velocità istantanea all’istante “t” (m/s): v(t) = lim
=
t 0 t
dx
dt = x ˙ (t)
- Accelerazione media (m/s 2 ): a = v
t = v(t2 ) v(t1) t2 t1 - Accelerazione istantanea (m/s 2 v(t + t) v(t)
): a(t) = lim
=
t 0 t
dv
dt = v ˙ (t). NOTA: essendo
v(t) = dx / dt , l’accelerazione istantanea è la derivata seconda di x(t), cioè
a(t) = d dx
dt dt = d 2 x
dt 2 = x ˙ (t).
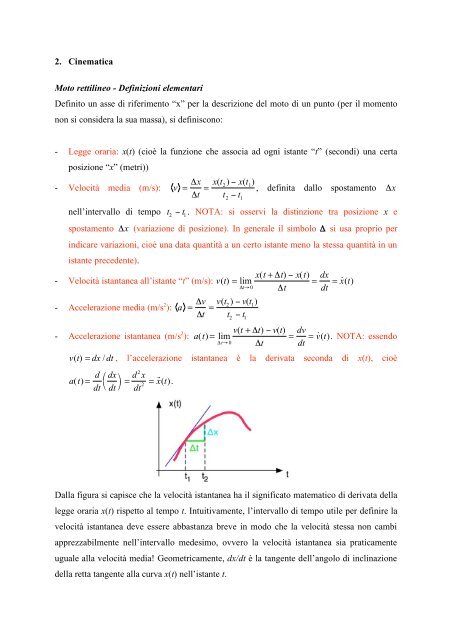
Dalla figura si capisce che la velocità istantanea ha il significato matematico di derivata della
legge oraria x(t) rispetto al tempo t. Intuitivamente, l’intervallo di tempo utile per definire la
velocità istantanea deve essere abbastanza breve in modo che la velocità stessa non cambi
apprezzabilmente nell’intervallo medesimo, ovvero la velocità istantanea sia praticamente
uguale alla velocità media! Geometricamente, dx/dt è la tangente dell’angolo di inclinazione
della retta tangente alla curva x(t) nell’istante t.

OSSERVAZIONI:
- Per brevità, il rapporto incrementale che individua la velocità istantanea è indicato con
dx/dt, e anche nel seguito del corso gli incrementi d(qualchecosa) indicheranno una
piccola variazione della grandezza “qualchecosa” in un intervallo di tempo infinitesimo
dt.
- Attenzione, dx/dt non è la stessa cosa di x/t !!!
- Come vedremo, indicando le derivate come fatto ad esempio per dx/dt permette di
svolgere molti calcoli in maniera semplice, trattando le quantità infinitesime dx e dt come
normali grandezze algebriche
Esempio: un’automobile che percorre un tratto di strada lungo 100 km in 2 ore ha una
velocità media di 50 km/h. Ciononostante, il tachimetro che indica la velocità istantanea
misurando la “velocità di rotazione delle ruote”, in vari istanti lungo il percorso potrà indicare
valori di velocità anche molto diversi: per esempio oltre 100 km/h in tratti rettilinei liberi e 20
km/h in tratti con lavori in corso…
Esempio: sia x(t)=3t 2 -2 (m), essendo t (s). La velocità media nell’intervallo 1s

Procedimento inverso: come calcolare v(t), x(t) nota l’accelerazione a(t)
Questo problema permette di introdurre il concetto di “integrale” per via geometrica, in
relazione a un problema fisico ben preciso.
Sia nota per esempio la velocità istantanea v(t) per ogni istante in un certo intervallo 0

Moto rettilineo uniforme
Velocità costante: v(t)=v0. Quindi a(t) = dv / dt =0. Al generico istante “t” si ha:
Moto rettilineo uniformemente accelerato
t
x(t) = x(0) + v0 dt = x(0 ) + v0 t
Accelerazione costante: a(t)=a 0. Al generico istante “t” si ha:
OSSERVAZIONI:
t
0
v(t) = v(0) + a0 dt = v(0) + a0 t
x(t) = x(0) + v(t) dt
t
0
0
= x(0)+ v(0)t + 1
2 a 0 t2
- si osservi l’importanza delle condizioni iniziali x(0), v(0). Si può facilmente verificare che
prendendo le derivate dx/dt e dv/dt si ottengono rispettivamente proprio le espressioni di
v(t) e a 0.
- Le espressioni ricavate per v e per x valgono solo per un moto ad accelerazione costante:
per esempio non si applicano a un moto armonico!!!
Esempio: un sasso è lanciato verticalmente verso l’alto con velocità v 0=9.8 m/s; calcolare la
massima quota raggiunta e in quanto tempo viene raggiunta. (accelerazione di gravità g=9.8
m/s 2 verso il basso)
Assumendo un asse di riferimento “x” diretto verso l’alto, con origine nel punto di partenza,
abbiamo:
v(t) = v 0 gt
x(t) = 0 + v0 t 1
2 gt2
La massima quota raggiunta corrisponde all’istante in cui la velocità cambia segno (da verso
l’alto, positiva, a verso il basso, negativa), cioè t=v0/g=1 s. Messo questo valore nella legge
oraria x(t) si ottiene x(1)=9.8-9.8/2=4.9 m.

Moto nel piano - Rappresentazione cartesiana del moto
r
Vettore posizione del punto P: r (t) = x(t) r
i + y(t) r
j
Il vettore posizione, al variare del tempo t, traccia la traiettoria del punto P.
y
r(t)
P
r(t+dt)
x
r
Il vettore velocità v (t) è tangente alla traiettoria in ogni istante, per definizione di traiettoria.
Il vettore spostamento infinitesimo d r = r (t + dt) r (t) è infatti tangente alla traiettoria come
si intuisce dal disegno.
Assegnate le leggi orarie x(t) e y(t), essendo d r = dx r
i + dy r
j si calcolano direttamente:
r
vettore velocità v (t) = vx(t) r
i + vy(t) r
j = d r / dt ; vx (t) = dx / dt , vy (t) = dy / dt
r
vettore accelerazione a (t) = ax (t) r
i + ay (t ) r
j = d r
v /dt ; a x (t) = dvx / dt , a y(t) = dvy / dt
r r
NOTA: I versori i , j non cambiano nel tempo.
Viceversa, assegnato il vettore r
a (t) e le condizioni iniziali del moto ( r
v (0) e r (0)) si
calcolano i vettori
velocità
posizione
r
v (t) = r
v (0) + r
a (t)dt
r (t) = r (0) + r
v (t) dt
dr
v(t)
t
t
0
= vx (0) + ax (t)dt
0
t
t
0
= x(0)+ vx (t)dt
0
t
r
r
i + vy (0) + ay (t)dt
j
t
r
r
i + y(0) + vy (t)dt
j
0
0

Esempio: Moto del proiettile. Consideriamo un proiettile lanciato a velocità v 0 con angolo
rispetto al piano orizzontale. Calcoliamo la gittata L (massima distanza percorsa lungo “x”) e
la massima altezza H raggiunta.
Essendo a y=-g, v x(0)=v 0cos, v y(0)=v 0sin, x(0)=y(0)=0 usando le relazioni scritte sopra
abbiamo:
v x (t) = v 0 cos ; v y(t) = v 0 sin gt
x(t) = v0t cos ; y(t) = v0t sin 1
2 gt2
Massima gittata: quando il proiettile torna a terra, quindi y(tL)=0. Imponendo questa
2
condizione si ottiene tL = 2v0 sin / g , e infine L = x(t L ) = 2v0 sin cos / g . Si noti che la
gittata è massimizzata per =45°.
Massima quota raggiunta nella traiettoria: quando v y(t H)=0, cioè t H = v 0 sin / g e quindi
H = y(t H ) = v 0
2 sin 2
2g

Rappresentazione del moto riferita alla stessa traiettoria
Come sottinteso da quanto detto in precedenza, il vettore velocità istantanea può essere
definito in termini del vettore spostamento infinitesimo:
r
v (t) = d r / dt
r
Come detto prima, v (t) è tangente alla traiettoria e punta nella direzione di avanzamento.
r
Definendo un versore u T (t) tangente alla traiettoria e che punta nella direzione di
avanzamento (in generale variabile nel tempo se la traiettoria è curvilinea), si può scrivere:
r
v (t) = v(t) r
u T (t)
y
O
s(t)
r(t)
P
v(t)=v(t)u T
Il modulo del vettore velocità, cioè v(t) , si chiama velocità scalare e rappresenta la rapidità
con cui viene percorsa una traiettoria (è il dato indicato dal tachimetro di un’auto). Misurando
la strada fatta s(t) lungo una certa traiettoria a partire da un riferimento di partenza O, si ha:
v(t) = ds / dt
r
Il vettore accelerazione a (t) nel piano ha invece sempre due componenti:
- tangente alla traiettoria: indica se cambia la rapidità di percorrenza (es.: se cambia la
velocità indicata dal tachimetro dell’auto)
- normale alla traiettoria e verso l’interno della curva (“centripeta”): indica semplicemente
la variazione di direzione della traiettoria (es.: un’auto in curva con velocità costante
indicata dal tachimetro “sente” un’accelerazione, cioè gli occupanti si sentono “spinti
ortogonalmente alla traiettoria” diversamente da quanto avviene su un rettilineo a velocità
costante!)
In sintesi, il vettore velocità può variare (e quindi dar luogo ad una accelerazione) se si
verifica almeno uno di questi fatti:
r
- cambia il modulo del vettore v (t) (“tachimetro”)
r
- cambia la direzione del vettore v (t), anche se il suo modulo resta costante (curva con
“tachimetro che indica velocità costante”)
x

Per calcolare l’espressione generale del vettore accelerazione riferito alla traiettoria
definiamo alcune quantità:
- raggio di curvatura della traiettoria, R = raggio della circonferenza (di centro C) che
meglio approssima la traiettoria vicino alla posizione istantanea del punto P.
r
r
- versore normale, u N (t) , orientato perpendicolare alla traiettoria (e quindi a u T(t) ) e
diretto verso il centro C.
- angolo d al centro della circonferenza associato alla percorrenza di un tratto ds = Rd
r
di traiettoria. Come si vede dal disegno, è lo stesso angolo di cui ruota il versore u T (t)
nell’intervallo di tempo dt.
Procediamo secondo la definizione:
r
a = dr
r
v d(v u T )
= =
dt dt
dv r
u T + v
dt
dr u T
dt
(si è sfruttata la regola di derivazione di un prodotto di funzioni, che vale anche nel calcolo
vettoriale, facendo attenzione al fatto che la derivata di un vettore è un vettore!)
Dalla figura precedente, si ha d r
u T = d r
u N = (ds / R) r
u N , per cui:
Le due componenti di
precedenza.
OSSERVAZIONI:
u T
r
a = dv r
u T + v
dt
dr
dt
= dv
dt
r
u T + v
R
ds
dt
r r r
a = aT u T + aN u N = dv
2
r v r
u T + u N
dt R
r
a (t) hanno pertanto il significato discusso intuitivamente in
- la componente normale (centripeta, ossia diretta verso il centro C) in generale c’è sempre
se la traiettoria è curva (R finito e v0). Nel moto del proiettile esaminato prima
evidentemente questa componente c’è sempre, diretta verso la “pancia” della parabola
- la componente tangenziale è non nulla solo se la velocità scalare cambia (cioè se il
“tachimetro” indica variazioni del modulo della velocità). Nel caso del moto del
r
u N

proiettile, questa componente è nella direzione del moto o opposta a seconda che il
proiettile stia salendo o scendendo
- il moto rettilineo corrisponde a R = , quindi c’è solo la componente tangenziale!
Moto circolare
Il raggio di curvatura R è evidentemente costante in tutti i punti della traiettoria
(circonferenza), e il centro di curvatura è fissato. Valgono tutte le considerazioni fatte nel
caso generale del moto curvilineo per le componenti dell’accelerazione.
Un caso particolare è quello del moto circolare uniforme (velocità scalare costante):
v(t) = v0 r
a (t) = v 2
0 r
u N
R
Si noti che c’è solo accelerazione centripeta.
Nel caso del moto circolare si definisce un vettore velocità angolare r
:
r
= = d
dt ,
r
= r
k
il cui modulo rappresenta la rapidità di percorrenza angolare della circonferenza (rad/s), e la
cui direzione è, per definizione, normale al piano della circonferenza e secondo la regola
della mano destra (dita piegate a descrivere il senso del moto e pollice che definisce il verso
di r
, normale al piano della circonferenza)
Considerando un moto circolare (anche non uniforme) in un sistema di riferimento xyz
arbitrario, si può verificare che r
v = r
r
Si può definire anche un vettore accelerazione angolare r
(rad/s 2 ):
r
= d v
dt