La parabola.pdf

ISTITUTO PROVINCIALE DI CULTURA E LINGUE “NINNI CASSARÀ” – SEDE DI VIA FATTORI
CORSI I.D.E.I. - LA PARABOLA
CLASSI QUARTE
Prof. E. Modica
erasmo@galois.it
www.galois.it
DEFINIZIONI
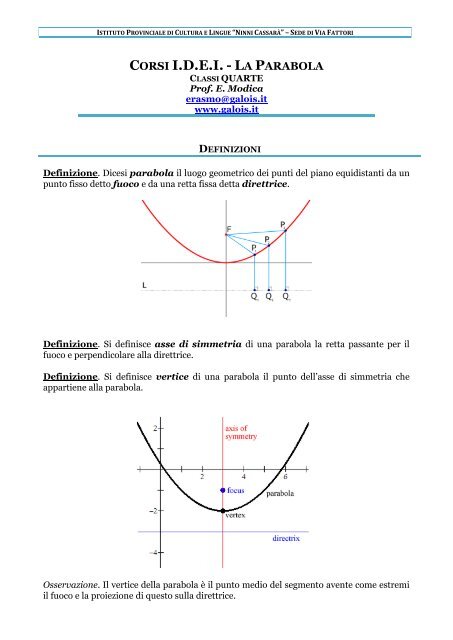
Definizione. Dicesi parabola il luogo geometrico dei punti del piano equidistanti da un
punto fisso detto fuoco e da una retta fissa detta direttrice.
Definizione. Si definisce asse di simmetria di una parabola la retta passante per il
fuoco e perpendicolare alla direttrice.
Definizione. Si definisce vertice di una parabola il punto dell’asse di simmetria che
appartiene alla parabola.
Osservazione. Il vertice della parabola è il punto medio del segmento avente come estremi
il fuoco e la proiezione di questo sulla direttrice.

Si dimostra che l’equazione di una generica parabola è la seguente:
con { }.
Teorema. Ogni equazione del tipo , con { }, rappresenta una
parabola avente:
vertice in (
fuoco in (
direttrice di equazione
asse di simmetria di equazione
E. Modica, 2011/2012
www.galois.it
)
)
STUDIO DI UNA PARABOLA
Tracciamo il grafico della parabola di equazione:
Vertice
Utilizzando le formule date nel teorema precedente si ha:
( )
( )
Per determinare l’ordinata del vertice, basta sostituire il valore dell’ascissa nell’equazione
della parabola. Si ha:
( ) ( )
Quindi il vertice ha coordinate: ( )
Fuoco
L’ascissa del fuoco è uguale a quella del vertice:
Il dell’equazione è dato da:
Quindi l’ordinata del fuoco è:
( ) ( )( )
( )
2

Le coordinate de fuoco sono: (
Direttrice
L’equazione della direttrice è data da:
Asse di simmetria
E. Modica, 2011/2012
www.galois.it
)
( )
L’asse di simmetria della parabola ha equazione:
Intersezioni con gli assi
Per determinare le intersezioni con l’asse delle ascisse bisogna risolvere il sistema:
da cui si ha l’equazione:
ossia:
Essendo:
le soluzioni saranno:
Quindi i punti d’intersezione della parabola con l’asse delle ascisse sono:
{
(
)
( √ ) ( √ )
Per determinare le intersezioni con l’asse delle ordinate bisogna risolvere il sistema:
{
√
3

da cui, sostituendo, si ha:
Quindi il punto d’intersezione della parabola con l’asse delle ordinate è:
E. Modica, 2011/2012
www.galois.it
( )
4

RELAZIONE TRA I COEFFICIENTI DI UNA PARABOLA E IL SUO GRAFICO
COEFFICIENTE RELAZIONE GRAFICO
a
b
c
E. Modica, 2011/2012
www.galois.it
Ci dà informazioni sulla concavità
della parabola. Se , allora la
concavità è rivolta verso l’alto; se
, essa è rivolta verso il basso.
Rende conto dello spostamento
dell’asse della parabola. Se b
aumenta l’asse si sposta verso
sinistra, se b diminuisce l’asse si
sposta verso destra.
Rende conto dello spostamento del
punto d’intersezione della parabola
con l’asse delle ordinate.
5

RELAZIONE TRA IL DISCRIMINANTE E LE INTERSEZIONI CON L’ASSE DELLE ASCISSE
DISCRIMINANTE INTERSEZIONI EVENTUALI GRAFICO
E. Modica, 2011/2012
www.galois.it
La parabola ha due punti di
intersezione distinti con l’asse delle
ascisse.
La parabola ha due punti di
intersezione con l’asse delle ascisse
coincidenti, ossia la parabola è
tangente all’asse delle ascisse.
La parabola non interseca l’asse
delle ascisse.
MUTUA POSIZIONE FRA RETTA E PARABOLA
Per studiare la mutua posizione tra una retta e una parabola basta risolvere il seguente
sistema:
{
Si possono verificare i tre casi illustrati nella seguente tabella, in base al valore del
discriminante del sistema.
6

DISCRIMINANTE POSIZIONE GRAFICO
Data la parabola di equazione:
E. Modica, 2011/2012
www.galois.it
La retta e la parabola sono
secanti.
La retta e la parabola sono
tangenti.
La retta e la parabola sono
esterne.
TANGENTE A UNA PARABOLA IN UN SUO PUNTO
sia ( ) un suo punto.
Per determinare l’equazione della retta tangente alla parabola nel suo punto P, si procede
come segue:
1) si scrive l’equazione del fascio proprio di rette passante per ( ), cioè:
( )
2) si determina il coefficiente angolare della retta tangente utilizzando la seguente
formula:
essendo i coefficienti della parabola e l’ascissa del suo punto P.
7

Esempio. Scrivere l’equazione della retta tangente alla parabola di equazione:
nel suo punto ( ).
Scriviamo l’equazione del fascio di rette passante
per il punto P:
E. Modica, 2011/2012
www.galois.it
( )
Determiniamo il coefficiente angolare della retta
tangente alla parabola nel punto dato:
( )( ) ( )
L’equazione della retta tangente è quindi:
Ossia:
( )
TANGENTI A UNA PARABOLA CONDOTTE DA UN PUNTO ESTERNO A ESSA
Data la parabola di equazione:
sia ( ) un punto che non appartiene a essa.
Per determinare l’equazione della retta tangente alla parabola nel suo punto P, si procede
come segue:
1) si scrive l’equazione del fascio proprio di rette passante per ( ), cioè:
( )
2) si considera il sistema formato dalla parabola e dal fascio proprio di rette:
3) si pone uguale a zero il discriminante del sistema:
{
( )
( )
4) si sostituiscono i valori trovati nell’equazione del fascio proprio di rette.
8

Esempio. Scrivere le equazioni delle rette tangenti alla parabola di equazione:
nel suo punto ( ).
Scriviamo l’equazione del fascio di
rette passante per il punto P:
E. Modica, 2011/2012
www.galois.it
( )
Consideriamo il sistema:
{
da cui si ricava l’equazione:
ovvero:
Raccogliendo si ottiene l’equazione:
Il discriminante è dato dall’espressione:
( ) ( )
Imponendo , si ottiene:
Risolvendo:
( )
Quindi le equazioni delle rette tangenti sono:
√
( √ ) ( √ ) ( √ ) ( √ )
9