Coordinate cartesiane nello spazio - Aula Digitale

capitolo
2
1
Coordinate cartesiane
Coordinate cartesiane nello spazio
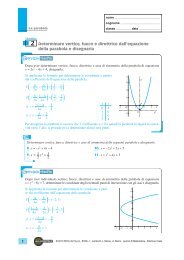
Nello spazio si considerino tre rette passanti per il punto O e a due a due ortogonali, dette
asse x o asse delle ascisse, asse y o asse delle ordinate, asse z o asse delle quote.
Fissata una unità di misura u e orientati gli assi, il riferimento cartesiano si dice destro se
l’orientamento è come in figura 1, si dice sinistro se è come in figura 2.
x
O
■ Figura 1 ■ Figura 2
A ogni punto P restano associati i punti P x , P y , P z ,
intersezioni rispettivamente con l’asse x del piano
per P parallelo al piano yz, con l’asse y del piano per
P parallelo al piano xz, con l’asse z del piano per P
parallelo al piano xy (fig. 3); siano x, y, z le coordinate
dei tre punti così ottenuti sui rispettivi assi: il
numero x prende il nome di ascissa, y di ordinata
e z di quota di P e si scrive P(x; y; z).
L’origine O ha le coordinate tutte nulle.
A ogni punto P resta così associata una terna ordinata di numeri reali (x; y; z); viceversa
a ogni terna ordinata di numeri reali (x; y; z) resta associato il punto P ottenuto come intersezione
dei tre piani passanti per P x (x), P y (y), P z (z) e rispettivamente paralleli ai piani
coordinati yz, xz, xy.
I piani coordinati dividono lo spazio in otto triedri detti ottanti.
La condizione sulle coordinate relativa all’appartenenza di P(x; y; z) a uno dei piani o degli
assi coordinati è riportata nelle tabelle seguenti:
Piano
xy z = 0
yz x = 0
xz y = 0
z
Dette P xy , P yz , P xz le proiezioni ortogonali di P(x; y; z)
rispettivamente sui piani xy, yz, xz (fig. 4), risulta:
Pxy (x; y; 0)
Pyz (0; y; z)
Pxz (x; 0; z)
y
Asse
x y = z = 0
y x = z = 0
z x = y = 0
© 2010 RCS Libri S.p.A., ETAS - L. Lamberti, L. Mereu, A. Nanni - Corso di Matematica - Edizione mista
y
z
O
x
P x
x
P xz
P x
O
z
P z
O
z Pz
P
P y
P
P xy
x
■ Figura 4
P yz
P y
y
■ Figura 3
y

capitolo
2
2
Coordinate cartesiane
Simmetrie
Dato P(x; y; z), risulta quanto riportato nella
tabella a fianco.
Distanza tra due punti
Calcoliamo la distanza di P(x; y; z) dall’origine
O(0; 0; 0).
Considerato il punto Pxy (fig. 5), applicando
il teorema di Pitagora al triangolo rettangolo
OPxyP, risulta:
–––
OP2
–––
= OP2xy
––––
+ PxyP2 Considerato poi il punto Px , applicando il teorema
di Pitagora al triangolo rettangolo
OPxPxy , risulta:
–––
OP2xy
–––
= OP2x
––––
+ PxP2xy Pertanto:
–––
OP2
–––
= OP2x
––––
+ PxP2xy ––––
+ PxyP2 = x2 + y2 + z2 e quindi:
[1]
Calcoliamo, ora, la distanza tra due punti
A(x A ; y A ; z A ) e B(x B ; y B ; z B ).
Sia H il punto d’intersezione del piano per A
parallelo al piano xy con la retta per B perpendicolare
al piano xy (fig. 6).
Essendo:
si ha:
OP = x2 + y2 + z2
AH = A B = ( x − x ) 2 + ( y −y)
2 e AB = AH + HB
xy xy A B A B
AB = ( x − x ) + ( y − y ) + ( z −z)
2 2 2
A B A B A B
Punto medio di un segmento. Baricentro di un triangolo
Dati i punti A(x A ; y A ; z A ) e B(x B ; y B ; z B ), il punto medio M ha coordinate:
xA + xB; 2
yA + yB; 2
zA + zB
2
[3]
Il baricentro G del triangolo che ha come vertici i punti A(xA ; yA ; zA ), B(xB ; yB ; zB ),
C(xC ; yC ; zC ) ha coordinate:
x + x + x y + y + y z + z + z
; ;
3 3 3
A B C A B C A B C
Simmetria Simmetrico di P
piano xy (x; y; –z)
piano yz (–x; y; z)
piano xz (x; –y; z)
origine O (–x; –y; –z)
2 2 2
© 2010 RCS Libri S.p.A., ETAS - L. Lamberti, L. Mereu, A. Nanni - Corso di Matematica - Edizione mista
x
P x
x
z
O
■ Figura 5
z
O
A
A xy
■ Figura 6
P
P xy
B
H
B xy
P y
y
y
[2]
[4]