Vettori Complessi e Polarizzazione (pdf 221K) - Nettuno
Vettori Complessi e Polarizzazione (pdf 221K) - Nettuno
Vettori Complessi e Polarizzazione (pdf 221K) - Nettuno
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
Facoltà di Ingegneria<br />
Corso di laurea in Scienze per l’Ingegneria<br />
Dispense per il corso di Campi Elettromagnetici I<br />
Prof. Fabrizio Frezza<br />
<strong>Vettori</strong> complessi e polarizzazione<br />
Università “LaSapienza”diRoma<br />
ROMA A.A. 2003-2004
Introduzione 1<br />
Introduzione<br />
L’utilizzo dei vettori complessi in elettromagnetismo è legato allo studio di campi vettoriali che<br />
hanno una dipendenza temporale di tipo armonico. Si consideri un generico campo vettoriale<br />
F(t) che soddisfi l’equazione dei moti armonici:<br />
d 2<br />
dt 2 F(t)+ω2 F(t) =0 (ω 2 > 0) (1)<br />
E’ noto che una soluzione della (1) può essere scritta nella forma:<br />
F(t) =F1 cos ωt + F2 sin ωt (2)<br />
con F1 e F2 vettori reali indipendenti dal tempo. Fissata la pulsazione ω è immediato stabilire<br />
una corrispondenza biunivoca fra le soluzioni della (1) e vettori della forma f = fr +jfj:<br />
F(t) R<br />
−→ f : f = F(0) − j F(π/2ω) (3)<br />
f R−1<br />
−→ F(t) : F(t) = ℜe fe j ωt = fr cos ωt − fj sin ωt (4)<br />
E’ evidente che f ∈ C 3 può essere sempre decomposto nelle sue parti reale e immaginaria fr,fj<br />
∈ R3 echeRe R−1 sono l’una l’inversa dell’altra. Dalle (3) e(4) si deduce facilmente che:<br />
⎧<br />
⎪⎨ fr = F1<br />
⎪⎩ fj = −F2<br />
e<br />
⎧<br />
⎪⎨ F1 = fr<br />
⎪⎩ F2 = −fj<br />
(5)<br />
Es.1 Dato F(t) = 2cosωt ˆx +3cosωt ˆy − 5sinωt ˆz si determini il corrispondente vettore<br />
complesso.<br />
Dopo aver messo in evidenza la dipendenza temporale:<br />
F(t) =(2ˆx +3ˆy)cosωt +(−5 ˆz)sinωt<br />
si deducono F1 = F(0) = (2 ˆx +3ˆy) eF2 = F(π/2ω) =−5 ˆz e utilizzando la (3) si ottiene<br />
immediatamente il vettore complesso cercato:<br />
f = F1 − j F2 =2ˆx +3ˆy +j5ˆz
2<br />
Es.2 Dato F(t) = 2cosωt + π/4 ˆx +3cosωt − π/4 ˆz si determini il corrispondente vettore<br />
complesso. utilizzando la (3) si ottiene immediatamente il vettore complesso cercato:<br />
da cui<br />
F(0) = 2 cos π/4 ˆx +3cos−π/4 ˆz = √ 2 ˆx + 3√<br />
2 ˆz<br />
2<br />
F(π/2ω) =2cosπ/2+π/4 ˆx +3cosπ/2 − π/4 ˆz = − √ 2 ˆx + 3√<br />
2 ˆz<br />
2<br />
f =( √ 2 ˆx + 3√<br />
√ 3√<br />
2 ˆz)+j( 2 ˆx − 2 ˆz)<br />
2<br />
2<br />
E’ bene notare che in elettromagnetismo si considerano anche vettori complessi che non rap-<br />
presentano un vettore variabile sinusoidalmente nel dominio del tempo. Esempi sono il vettore<br />
di propagazione k = β − j α delle onde piane e il vettore di Poynting nel dominio dei fasori<br />
P = 1<br />
2 E × H∗ .<br />
Ellisse di polarizzazione<br />
E’ naturale chiedersi quale sia il luogo geometrico descritto da F(t) pensato come vettore<br />
applicato nell’origine di R 3 .<br />
F(t) è una funzione periodica di periodo T =(2π/ω) di classe C ∞ , dunque il luogo è una<br />
curva regolare e chiusa, inoltre è limitata poiché |F(t)| ≤|F1 cos ωt| + |F2 sin ωt| ≤|F|1 + |F2|.<br />
• Se F1 × F2 = 0, che comprende i casi F1 = 0 e F2 = 0, sihacheF(t) è sempre parallelo<br />
a F1 e/o F2, descrivendo un segmento di semiampiezza |F 2 1 | + |F2 2 |.<br />
• Se F1 × F2 = 0, F(t) è combinazione lineare dei vettori F1, F2 che sono non nulli e<br />
non paralleli, pertanto F(t) giace sempre nel piano formato da F1 e F2 detto piano<br />
di polarizzazione. Stabilendo in questo piano un sistema di riferimento cartesiano e<br />
proiettando F(t) lungo gli assi coordinati si ottiene un sistema di equazioni, che dà luogo,<br />
una volta eliminata la dipendenza dal tempo, ad un’equazione algebrica di secondo grado<br />
nelle componenti Fx e Fy. La conica così ottenuta deve avere punti reali al finito in un<br />
dominio limitato e dunque non può che essere un’ellisse.<br />
• Se |F1| = |F2| e F1 · F2 = 0 l’ellisse è un cerchio e F(t) non dipende dal tempo.<br />
Poiché |F(t)| 2 = |F1| 2 cos 2 ωt+ |F2| 2 sin 2 ωt+2F1 · F2 cos ωt sin ωt è evidente che se sono<br />
verificate le condizioni precedenti risulta |F(t)| 2 = |F1| 2 + |F2| 2 indipendente dal tempo.<br />
Viceversa se |F(t)| non dipende da t, allora |F(0)| 2 = |F1| 2 = |F(π/2ω)| 2 = |F2| 2 .
Ellisse di polarizzazione 3<br />
Dunque |F(t)| 2 = |F1| 2 + F1 · F2 sin 2ωt che può essere indipendente dal tempo solo se<br />
F1 · F2 =0.<br />
Il caso F1 × F2 = 0 è detto di polarizzazione lineare (LP).Ilcaso|F1| = |F2| e F1 · F2 =0è<br />
detto di polarizzazione circolare (CP). Tutti gli altri casi, invece, sono detti di polarizzazione<br />
ellittica (EP). E’ evidente che LP e CP sono casi particolari di polarizzazione ellittica.<br />
Si è visto come tramite la (3) sia possibile associare a F(t) un vettore complesso f = fr +jfj.<br />
E’ possibile caratterizzare la polarizzazione in termini dei componenti fr e fj. Nel caso di<br />
polarizzazione lineare si ha fr × fj = 0 per quanto già visto. Si osservi che se in questo caso si<br />
può scrivere fr = fr û e fj = fj û, con û ∈ R 3 e | û| = 1; dunque f = fr+j fj =(fr+j fj) û = c û<br />
con c ∈ C. Viceversa, se f = c û con c ∈ C e û versore reale, risulta evidentemente fr × fj = 0,<br />
dunque polarizzazione lineare. Allo stesso modo, per quanto già detto, la polarizzazione<br />
circolare si traduce nelle condizioni |fr| = |fj| e fr · fj = 0 che sono equivalenti a f · f =0. In<br />
tutti i casi in cui non sono verificate le condizioni per LP e CP si ha polarizzazione ellittica.<br />
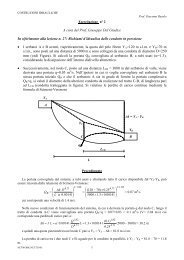
b<br />
y ′<br />
y<br />
(a)<br />
α<br />
a<br />
x ′<br />
x<br />
Figura 1: ellisse di polarizzazione<br />
Per ricavare esplicitamente l’equazione dell’ellisse di polarizzazione si fissa, come si è detto, un<br />
sistema di riferimento cartesiano nel piano di polarizzazione. In questo sistema si potrà scrivere<br />
f = fx ˆx + fy ˆy, confx = ˆ fxe j φx e fy = ˆ fye j φy numeri complessi. Dunque fr = ˆ fx cos φx ˆx +<br />
ˆfy cos φy ˆy e fj = ˆ fx sin φx ˆx + ˆ fy sin φy ˆy, mainvirtù della (4)<br />
b<br />
F(t) =( ˆ fx cos φx ˆx + ˆ fy cos φy ˆy)cosωt − ( ˆ fx sin φx ˆx + ˆ fy sin φy ˆy)sinωt (6)<br />
Proiettando lungo gli assi coordinati si ottiene il sistema:<br />
⎧<br />
⎪⎨ Fx =<br />
⎪⎩<br />
ˆ fx cos φx cos ωt − ˆ fx sin φx sin ωt<br />
Fy = ˆ fy cos φy cos ωt − ˆ fy sin φy sin ωt<br />
y ′<br />
(b)<br />
a<br />
x ′<br />
(7)
4<br />
Per eliminare la dipendenza dal tempo, nella prima delle (7) siponeξ =sinωt. Quadrando è<br />
possibile scrivere un’equazione di secondo grado in ξ:<br />
Fx<br />
ˆfx<br />
2 +sinφxξ =cos 2 φx(1 − ξ 2 ) (8)<br />
ovvero<br />
ξ 2 +2 Fx<br />
<br />
Fx<br />
2<br />
ξ + − cos<br />
ˆfx<br />
ˆfx<br />
2 la cui soluzione fornisce:<br />
φx =0 (9)<br />
ξ =sinωt = − Fx<br />
sin φx ±<br />
ˆfx<br />
1<br />
<br />
ˆf<br />
ˆfx<br />
2 x − F 2 x cos φx<br />
Per cos ωt si ripete il ragionamento :<br />
(10)<br />
cos ωt = Fx<br />
cos φx ±<br />
ˆfx<br />
1<br />
<br />
ˆf<br />
ˆfx<br />
2 x − F 2 x sin φx<br />
(11)<br />
Sotituendo queste due espressioni nella seconda delle (7), quadrando e riordinando i termini<br />
si ha:<br />
ˆf 2 xF 2 y + ˆ f 2 y F 2 x − 2 ˆ fx ˆ fyFxFy cos φ = ˆ f 2 x ˆ f 2 y sin 2 φ, φ = φy − φx (12)<br />
che è l’equazione di un’ellisse con semiassi ruotati di un certo angolo α rispetto agli assi<br />
x e y del sistema di riferimento fissato sul piano di polarizzazione. A volte può risultare<br />
conveniente scrvere l’equazione dell’ellisse in forma canonica; a questo scopo è possibile operare<br />
una rotazione degli assi proprio dell’angolo α:<br />
⎧<br />
⎪⎨ x<br />
⎪⎩<br />
′ = x cos α + y sin α<br />
y ′ = −x sin α + y cos α<br />
Si ottiene così la nuova rappresentazione:<br />
( ˆ f 2 x sin2 α + ˆ f 2 y cos2 α − ˆ fx ˆ fy sin 2α cos φ)F ′2<br />
x +<br />
+( ˆ f 2 x cos2 α + ˆ f 2 y sin2 α + ˆ fx ˆ fy sin 2α cos φ)F ′2<br />
y +<br />
+( ˆ f 2 x sin 2α − ˆ f 2 y sin 2α − 2 ˆ fx ˆ fy cos 2α cos φ)F ′ xF ′ y =<br />
= ˆ f 2 x ˆ f 2 y sin 2 φ<br />
dove F ′ x e F ′ y sono le componenti del campo vettoriale considerato riferite al nuovo sistema di<br />
assi. Se<br />
tan 2α = 2 ˆ fx ˆ fy cos φ<br />
ˆf 2 x − ˆ f 2 (15)<br />
y<br />
allora l’ellisse viene riferita ad un sistema di assi paralleli ai suoi assi principali e con centro<br />
nel centro dell’ellisse. L’angolo di rotazione sarà:<br />
α = 1<br />
2 arctan 2 ˆ fx ˆ fy cos φ<br />
ˆf 2 x − ˆ f 2 y<br />
(13)<br />
(14)<br />
(16)
Caratterizzazione in termini delle componenti cartesiane nel piano di polarizzazione 5<br />
Rispetto al nuovo sistema di riferimento x ′ , y ′ , i semiassi dell’ellisse sono dati da<br />
eliminando α si ottiene<br />
a =<br />
b =<br />
Si definisce l’angolo di eccentricità come<br />
ˆfx ˆ fy| sin φ|<br />
ˆf 2 x sin 2 α + ˆ f 2 y cos 2 α − ˆ fx ˆ fy sin 2α cos φ<br />
ˆfx ˆ fy| sin φ|<br />
ˆf 2 x sin 2 α + ˆ f 2 y cos2 α + ˆ fx ˆ fy sin 2α cos φ<br />
√<br />
2fx ˆ<br />
a =<br />
ˆ fy| sin φ|<br />
<br />
( ˆ f 2 x + ˆ f 2 <br />
x ) − ( ˆ f 2 x + ˆ f 2 x )2 − 4 ˆ f 2 x ˆ f 2 y sin2 1/2 φ<br />
√<br />
2fx ˆ<br />
b =<br />
ˆ fy| sin φ|<br />
<br />
( ˆ f 2 x + ˆ f 2 <br />
x)+ ( ˆ f 2 x + ˆ f 2 x) 2 − 4 ˆ f 2 x ˆ f 2 y sin2 1/2 φ<br />
tan γ = ± b<br />
a<br />
il segno positivo si ha per φ>0, e cioè φy >φx se ˆ fx e ˆ fy sono positivi. Al tempo t =0si<br />
ha Fx(0) = ˆ fx cos φx e Fy(0) = ˆ fy cos φy. Questi valori sono supposti entrambi positivi. Se<br />
φy >φx, Fy(t) cambia segno allorché ωt = π/2 − φy, primacioè dell’istante in cui cambia<br />
segno Fx(t). Pertanto la polarizzazione è destrogira. Solitamente l’angolo di eccentricità si<br />
esprime attraverso<br />
sin 2γ = 2tanγ<br />
1+tan 2 γ = 2 ˆ fx ˆ fy sin φ<br />
ˆf 2 x + ˆ f 2 y<br />
Caratterizzazione in termini delle componenti cartesiane nel piano di polarizzazione<br />
Si consideri un sistema di riferimento con il piano xy coincidente con il piano di polarizzazione,<br />
cioè il piano individuato dai componenti fr e fj del vettore di polarizzazione f.<br />
LP Nel caso di polarizzazione lineare si èvistochesipuò scrivere f =(fr +jfj) û = c û con c ∈ C,<br />
û ∈ R 3 e | û| = 1. Dunque:<br />
fx =(fr +jfj)ux fy =(fr +jfj)uy = uy<br />
ux<br />
(17)<br />
(18)<br />
(19)<br />
(20)<br />
(21)<br />
(22)<br />
fx = rfx con r ∈ R (23)<br />
Si ha allora che fx e fy come numeri complessi sono in fase (arg fx − arg fy = 0), oppure<br />
in opposizione di fase (arg fx − arg fy = 0). Viceversa, se fx e fy sono in fase oppure in
6<br />
opposizione di fase, si può passare dall’uno all’altro moltiplicando per un numero r reale, ciè<br />
fy = rfy. Per cui<br />
f = fx ˆx + rfy ˆy = fx( ˆx + r ˆy) (24)<br />
e quindi f è il prodotto del numero complesso fx per un vettore reale, ossia è polarizzato<br />
linearmente. E’ possibile dire dunque:<br />
f polarizzato linearmente ⇐⇒ fx = rfy con r ∈ R (25)<br />
CP Allo stesso modo si procede per la polarizzazione circolare. In questo caso si èvistochetrai<br />
componenti del vettore di polarizzazione debbono sussistere le seguenti relazioni:<br />
|fr| = |fj| e fr · fj = 0 (26)<br />
Queste possono essere scritte in termini delle componenti rispetto al sistema di riferimento<br />
fissato nel piano di polarizzazione. ⎧⎪⎨<br />
⎪⎩<br />
f 2 rx + f 2 ry = f 2 jx + f 2 jy<br />
frxfjx + fryfjy =0<br />
Dalla seconda si ricava, quadrando, f 2 rx =(f2 ryf 2 jy )/f 2 . Sostituendo nella prima si ottiene:<br />
jx<br />
f 2 ry f 2 jy<br />
f 2 jx<br />
+ f 2 ry = f 2 jx + f 2 jy ⇒ f 2 ry (f 2 jy + f 2 jx )=f 2 rx (f 2 jy + f 2 jx ) ⇒ fry = ±fjx (28)<br />
Dalla seconda fryfjy = −frxfjx, dacuiseguefjy = ∓frx. Ma allora:<br />
fy = fry +jfjy = ±fjx ∓ j frx = ∓j fx<br />
Viceversa se fy = ±j fx segue fry +jfjy = ±j(frx +jfjx) =±frx ∓ fjx. Uguagliando parte<br />
reale e parte immaginaria si ottengono le relazioni fjy = ±frx e fry = ∓fjx. Utilizzando queste<br />
ultime è immediato verificare che fr · fj = frxfjx + fryfjy = ±fjyfjx ∓ fjxfjy =0einoltre<br />
|f 2 r | = f 2 rx + f 2 ry = f 2 jx + f 2 jy = |f 2 j |. Dunque:<br />
f polarizzato circolarmente ⇐⇒ fy = ±j fx<br />
In questo caso fx e fy, come numeri complessi, sono in quadratura (differenza di fase di π/2).<br />
EP Nel caso più generale di polarizzazione ellittica si avrà fy = Me j φ fx, conM,φ ∈ R e M>0.<br />
In particolare se M =1eφ = ±π/2 si ha polarizzazione circolare. Il caso in cui φ = ±π/2,<br />
ma M = 1 corrisponde ad una polarizzazione ellittica in cui gli assi principali dell’ellisse<br />
coincidono con gli assi cartesiani. Se invece φ = ±π/2 (e ovviamente anche φ = 0,π caso di<br />
polarizzazione lineare) si tratta di un’ellisse con gli assi principali ruotati di un certo angolo<br />
rispetto agli assi cartesiani.<br />
(27)<br />
(29)<br />
(30)
Verso di percorrenza dell’ellisse 7<br />
Verso di percorrenza dell’ellisse<br />
L’ellisse di polarizzazione viene percorsa nel verso secondo cui il vettore fj ruotando si so-<br />
vrappone al vettore fr percorrendo l’angolo minore (vedi Fig. 2(a)). In base a quanto detto<br />
è possibile classificare le onde piane in base al senso di rotazione dei campi elettromagnetici:<br />
un’onda piana si dice polarizzata (CP o EP) destra se il vettore campo elettrico (campo ma-<br />
gnetico) ruota in verso orario guardando nella direzione di propagazione; viceversa l’onda è<br />
detta polarizzata sinistra.<br />
fj<br />
(a)<br />
−fj<br />
fr<br />
Figura 2: (a) determinazione del verso di percorrenza dell’ellisse; (b) onda piana polarizzata<br />
CP o EP destra<br />
Parametri di Stokes<br />
Si considerino due campi elettrici sinusoidali, i cui fasori siano dati da<br />
⎧<br />
⎪⎨ ex = axe<br />
⎪⎩<br />
j φx ˆx<br />
ey = aye j φy ˆy.<br />
Nel dominio del tempo, a questi fasori corrispondono i campi<br />
⎧<br />
⎪⎨ Ex = ax cos (ωt + φx) ˆx<br />
⎪⎩ Ey = ay cos (ωt + φy) ˆy<br />
Si può eliminare il parametro temporale, come si è visto in precedenza, ottenendo<br />
2 Ex<br />
ax<br />
+<br />
2 Ey<br />
ay<br />
(b)<br />
k<br />
(31)<br />
(32)<br />
− 2 Ex Ey<br />
cos φ =sin<br />
ax ay<br />
2 φ (33)<br />
dove φ = φy − φx. Presi Ex e Ey come assi coordinati, è evidente che l’estremo del vet-<br />
tore risultante descrive un’ellisse centrata in Ex = Ey = 0. Per individuare l’ellisse, cioè<br />
la polarizzazione dell’onda, è necessario fornire tre parametri, ad esempio le grandezze ax,
8<br />
ay e φ. Ovviamente, è anche possibile individuare la polarizzazione mediante un’opportuna<br />
combinazione dei precedenti parametri. Stokes suggerì di utilizzare i parametri così definiti:<br />
⎧<br />
Quadrando e sommando si ha<br />
s0 =a 2 x + a2 y = ExE ∗ x + EyE ∗ y<br />
⎪⎨ s1 =a 2 x − a 2 y = ExE ∗ x − EyE ∗ y<br />
s2 =2axay cos φ = ExE ∗ y + E ∗ xEy<br />
⎪⎩ s3 =2axay sin φ =j(ExE ∗ y − E∗ xEy). s 2 0 = s 2 1 + s 2 2 + s 2 3<br />
il che dimostra che solo tre dei parametri di Stokes sono tra loro indipendenti. Noti questi<br />
s1<br />
s3<br />
2α<br />
s0<br />
2γ<br />
Figura 3: sfera di Poincaré<br />
P (s1,s2,s3)<br />
parametri l’ellisse di polarizzazione è immediatamente individuata, essendo<br />
Dalle (15), (21) e(22) siha<br />
a 2 x = s0 + s1<br />
2<br />
,a 2 y = s0 − s1<br />
2<br />
tan 2α = s2<br />
, sin 2γ = s3<br />
s2<br />
(34)<br />
(35)<br />
, tan φ = s3<br />
. (36)<br />
s1<br />
,s0 = a<br />
s0<br />
2 + b 2<br />
(37)<br />
E’ evidente che s3 = s0 sin 2γ eches2 =tan2φ. Sostituendo queste relazioni nella (35) siha<br />
anche s1 = s0 cos 2γ cos 2α. I parametri di Stokes possono essere espressi, dunque, in termini<br />
degli angoli α e γ: ⎧⎪ ⎨<br />
⎪⎩<br />
s1 = s0 cos 2γ cos 2α<br />
s2 = s0 cos 2γ sin 2α<br />
s3 = s0 sin 2γ<br />
Poiché la polarizzazione lineare corrisponde a γ =0(b = 0), essa è caratterizzata da s3 =0.<br />
La polarizzazione circolare corrisponde invece a γ = ±π/4, per essa si ha s1 =s2 =0. In<br />
s2<br />
(38)
Parallelismo e perpendicolarità tra vettori complessi 9<br />
virtù della (35), al variare della polarizzazione dell’onda, cioè degli angoli γ e α, il punto di<br />
coordinare (s1,s2,s3) descrive una superficie sferica di raggio s0. La latitudine del punto è<br />
pari a 2γ elalongitudine a2α. Questasferaè detta sfera di Poincaré; ciascuno dei suoi punti<br />
corrisponde a uno stato di polarizzazione. In particolare, la polarizzazione lineare (s3 =0)è<br />
rappresentata dai punti all’equatore; la polarizzazione circolare (s1 = s2 = 0) dai due poli. La<br />
semisfera superiore corrisponde alle polarizzazioni destre, quella inferiore alle polarizzazioni<br />
sinistre.<br />
Parallelismo e perpendicolarità tra vettori complessi<br />
E’ importante ricordare che un vettore complesso non può essere disegnato in R 3 ; esso in-<br />
fatti rappresenta, in generale, un vettore polarizzato ellitticamente nel dominio del tempo.<br />
Tuttavia, è possibile parlare di parallelismo e perpendicolarità in senso algebrico, secondo cui<br />
g = αf ,α∈ C parallelismo tra f e g<br />
g · f = 0 perpendicolarità traf e g<br />
Queste definizioni possono essere interpretate dal punto di vista geometrico.<br />
Sia g = αf, α = λej θ . Allora se f R−1<br />
−→ F(t) siha<br />
αf R−1<br />
−→ ℜe αf e j ωt <br />
= ℜe λf e j(ωt+θ)<br />
<br />
j<br />
= λ ℜe f e<br />
ω(t+θ/ω)<br />
= λF(t + θ/ω) (40)<br />
Dunque G(t) =λF(t + θ/ω); se F(t) è polarizzato secondo una certa ellisse (eventualmente<br />
una circonferenza o nel caso limite un segmento) G(t) sarà polarizzato secondo un’ellisse<br />
omotetica con rapporto di omotetia λ, percorsa con anticipo di θ/ω. La forma dell’ellisse<br />
(rapporto tra i semiassi), le direzioni degli assi principali e il verso di percorrenza rimangono<br />
invariati. Si giunge alla conclusione che la moltiplicazione di un vettore complesso per uno<br />
scalare complesso non cambia il tipo di polarizzazione.<br />
g f<br />
G(t)<br />
Figura 4: interpretazione geometrica del parallelismo tra vettori complessi<br />
Il contenuto geometrico della perpendicolarità è meno immediato. Dato un vettore complesso<br />
f = 0 sicerchiilpiù generale vettore g che sia ad esso perpendicolare. Se f èLP,g può<br />
F(t)<br />
(39)
10<br />
essere un vettore arbitrario del piano perpendicolare alla direzione di polarizzazione di f; cioè<br />
se f = α û, con û ∈ R 3 , allora g = û × h, conh arbitrario. Se f non èLP,esisteràunversore<br />
n ortogonale al piano di polarizzazione di f. Posto g = βn + gf con gf nel piano di f, si<br />
ha (βn · f) = 0 per ogni β. Resta da determinare gf in modo che risulti anche gf · f =0.<br />
Dall’identità<br />
gf × (n × f) =n(gf · f) − f(gf · n) (41)<br />
si ha, poiché gf ·f =0en·gf =0,chegf ×(n×f) =0. Dunque il più generale g perpendicolare<br />
a f ha la forma g = βn+αn×f, conα costante arbistraria. Il corrispondente G(t)è la somma<br />
di un vettore LP nella direzione di n ediunvettorenonLPnelpianodif, che ha ellisse di<br />
polarizzazione ortogonale a quella di f. Il più generale G(t) giace su un cilindro ellittico che<br />
ha sezione retta data da Gf (t) e generatrici parallele a n. Tagliando questo cilindro con piani<br />
arbitrari si ottengono tutte le possibili ellissi di polarizzazione dei vettori g perpendicolari a<br />
f. In particolare, esistono due vettori CP perpendicolari a f, che si determinano imponendo<br />
che g · g = 0. In questo modo si ottiene g = α(n × f ± j √ f · fn).<br />
g<br />
Figura 5: interpretazione geometrica del parallelismo tra vettori complessi<br />
n<br />
gf<br />
Rappresentazione assiale<br />
Per determinare rapidamente le dimensioni e le lunghezze degli assi principali dell’ellisse di<br />
polarizzazione associata ad un dato vettore complesso f, si considerino le seguenti proprietà<br />
dimostrate in precedenza:<br />
• g =e j θ f ha la stessa ellisse di f se θ ∈ R<br />
• ∃θ t.c. gr · gj =0<br />
• se gr · gj = 0, allora gr e gj giacciono sugli assi principali dell’ellisse.
Scomposizione di una generica polarizzazione 11<br />
se f èEPe √ f · f = 0 (per cui sicuramente f non è CP), si può scrivere<br />
fj<br />
gr<br />
(a)<br />
fr<br />
g = |√ f · f|<br />
√ f · f f (42)<br />
gj<br />
gr<br />
(b)<br />
Figura 6: costruzione della rappresentazione assiale<br />
Il vettore così ottenuto èdeltipog =e j θ f; essendo, inoltre, g · g ∈ R, sihagr · gj = 0, dunque<br />
gr e gj sono gli assi principali. Poiché g · g = |gr| 2 −|gj| 2 > 0, l’asse maggiore è gr, mentre<br />
l’asse minore è gj. Dalla g · g ∗ = f · f ∗ = |gr| 2 + |gj| 2 si trae un’interpretazione geometrica<br />
per |f| = |f · f ∗ |: essa è la lunghezza dell’ipotenusa del triangolo rettangolo che ha come cateti<br />
i semiassi dell’ellisse.<br />
Scomposizione di una generica polarizzazione<br />
Si è visto come sia possibile rappresentare un generico stato di polarizzazione come combina-<br />
zione di due polarizzazioni lineari; fissato un sistema di riferimento cartesiano xy sul piano di<br />
polarizzazione si può scrivere il vettore complesso f come somma dei due componenti fx ˆx e<br />
fy ˆy rispetto agli assi coordinati. Si ècioè utilizzata la base costituita dai vettori reali ˆx e<br />
ˆy per rappresentare il vettore complesso f. In molti casi pratici risulta, tuttavia, necessario<br />
espandere un dato vettore, reale o complesso, rispetto ad una base di vettori complessi. Un<br />
esempio è costituito dalla base ortonormale formata dalle due polarizzazioni circolari:<br />
c1 =<br />
ˆx − j ˆy<br />
√ 2<br />
, c2 =<br />
ˆx +j ˆy<br />
√ 2<br />
E’ facile verificare che c1 · c ∗ 2 = c2 · c ∗ 1 =0eche|c1| = |c2| = 1. Fissata questa base il vettore<br />
f = fx ˆx + fy ˆy si potrà scrivere f = f1c1 + f2c2, con<br />
f1 =(f · c ∗ 1)= fx +jfy<br />
√ 2<br />
|f|<br />
gj<br />
(43)<br />
e f2 =(f · c ∗ 2)= fx − j fy<br />
√ . (44)<br />
2<br />
Scomponendo una generica polarizzazione ellittica in due polarizzazioni circolari è semplice<br />
dedurre informazioni sull’ellisse di polarizzazione. Considerando, infatti, il rapporto tra le
12<br />
componenti rispetto a questa base<br />
f2<br />
f1<br />
= Me −j2α<br />
si può dimostrare che l’angolo α è l’angolo che gli assi principali dell’ellisse formano con gli<br />
assi cartesiani e che il rapporto tra il semiasse maggiore e quello minore èdatoda<br />
Si calcoli dunque il rapporto tra le componenti<br />
f2<br />
f1<br />
= (fx − j fy) 1<br />
√ 2<br />
fx +jfy) 1 √ 2<br />
b<br />
a<br />
= (fx − j fy)(f ∗ x − j f ∗ y )<br />
|fx +jfy| 2<br />
(45)<br />
|1+M|<br />
= . (46)<br />
|1 − M|<br />
= |fx| 2 −|fy| 2 − j2ℜe fxf ∗ <br />
y<br />
|fx +jfy| 2 . (47)<br />
In generale fx = ˆ fxe j φx e fy = ˆ fye j φy saranno complessi. Sostituendo nella precedente si<br />
ottiene<br />
Si avrà dunque<br />
f2<br />
f1<br />
= |fx| 2 −|fy| 2 − j2 ˆ fx ˆ fx cos φ<br />
|fx +jfy| 2 con φ = φy − φx. (48)<br />
α = − 1 f2<br />
arctan<br />
2 f1<br />
= 1<br />
2 arctan 2 ˆ fx ˆ fx cos φ<br />
|fx| 2 −|fy| 2<br />
analoga all’espressione determinata in precedenza per lo stesso angolo. In modo analogo si<br />
può dimostrare la validità dell’espressione per il rapporto tra i semiassi dell’ellisse.<br />
Identità di Gibbs<br />
Dato un vettore d ∈ C 3 può essere utile darne una rappresentazione in termini di altri tre<br />
vettori complessi a, b e c tali che a · b × c = 0 (condizione di indipendenza lineare). A questo<br />
scopo si consideri (a × b) × (c × d) =−(c × d) × (a × b) e si sviluppi il prodotto vettoriale:<br />
che può essere scritto anche come:<br />
(49)<br />
(a × b) × (c × d) =c[(a × b) · d] − d[(a × b) · c] (50)<br />
−(c × d) × (a × b) =−a[(c × d) · b]+b[(c × d) · a] (51)<br />
Uguagliando i secondi membri delle (50) e(51) si ottiene:<br />
d[(a × b) · c] =a[(c × d) · b] − b[(c × d) · a]+c[(a × b) · d] (52)<br />
Avendo supposto che i vettori a, b e c fossero linearmente indipendenti, è possibile dividere<br />
la (52) per(a × b) · c = 0 ottenendo un’espressione del vettore d in termini degli altri tre,<br />
detta identità di Gibbs:<br />
[(c × d) · b] × d) · a] × b) · d]<br />
d = a − b[(c + c[(a<br />
[(a × b) · c] [(a × b) · c] [(a × b) · c]<br />
(53)
Applicazione al caso della ionosfera 13<br />
aj<br />
90 ◦<br />
k<br />
ar<br />
A(t)<br />
Figura 7: k × a = k × (ar +jak) =ja<br />
Applicazione al caso della ionosfera<br />
Un caso interessante in cui la (53) può trovare applicazione è quello di un’onda piana uniforme<br />
che si propaga nella ionosfera dando luogo a due onde polarizzate circolarmente. E’ conveniente<br />
allora esprimere una generica onda in termini di queste due polarizzazioni. Indicando con a<br />
e a ∗ le due polarizzazioni circolari destra e sinistra entrambe perpendicolari al vettore di<br />
propagazione k dell’onda piana uniforme è possibile esprimere il vettore di polarizzazione del<br />
campo elettrico E in termini della terna a, a ∗ e k. Tenendo conto del fatto che k × a =ja e<br />
k × a ∗ = −j a ∗ ,èevidentecherisultak · a × a ∗ =ja · a ∗ = 0. Dunque sarà:<br />
ma<br />
E = a [(k × E) · a∗ ]<br />
[(a × a ∗ ) · k]<br />
[(k × E) · a]<br />
− a∗<br />
[(a × a∗ ) · k] + k[(a × a∗ ) · E]<br />
[(a × a∗ ) · k]<br />
[(k × E) · a ∗ ]=−E · k × a ∗ =jE · a ∗<br />
(54)<br />
(55)<br />
[(k × E) · a] =−E · k × a = −j E · a (56)<br />
[(a × a ∗ ) · k] =k × a · a ∗ =ja · a ∗<br />
(57)<br />
a × a ∗ =ja ∗ × (k × a) =j[k(a · a ∗ ) − a(k · a ∗ )] = j k(a · a ∗ ) (58)<br />
pertanto risulta<br />
E · a∗ E · a<br />
E = a + a∗ + k(E · k) (59)<br />
a · a∗ a · a∗ In particolare, per un’onda piana uniforme, risulta E·k = 0 e quindi la generica polarizzazione<br />
E viene scritta come somma di due polarizzazioni circolari. La ionosfera si comporta come un<br />
materiale isotropo che sotto l’azione di un campo magnetostatico di induzione B0 (in questo
14<br />
caso quello terrestre) diviene giroelettrico, ovvero anisotropo con costante dielettrica di tipo<br />
tensoriale (diadico). La direzione lungo cui agisce B0 costituisce un asse principale del tensore<br />
mentre gli altri due assi possono essere scelti ad arbitrio. Supponendo di aver fissato un sistema<br />
di riferimento cartesiano e scegliendo l’asse z nella direzione di B0 si ha:<br />
ovvero:<br />
⎛ ⎞ ⎛<br />
ɛ⊥<br />
⎜<br />
ɛ · E = ɛ0 ⎜ 0<br />
⎝<br />
0<br />
ɛ⊥<br />
0<br />
⎟ ⎜<br />
⎟ ⎜<br />
0 ⎟ ⎜<br />
⎠ ⎝<br />
0 0 ɛ Ex<br />
Ey<br />
Ez<br />
⎞<br />
⎟<br />
⎠ +jɛ0g ˆz × E (60)<br />
ɛ · E = ɛ0(ɛ⊥E⊥ +jg ˆz × E⊥)+ɛ0ɛ Ez ˆz (61)<br />
Si consideri un’onda piana uniforme che si propaga nella direzione e nel verso individuati<br />
dall’asse z con costante di propagazione β. Dalla prima equazione di Maxwell si avrà:<br />
e sostituendo nella seconda:<br />
H = β<br />
uz × E (62)<br />
ωµ0<br />
−β 2 ˆz × ( ˆz × E) =β 2 E⊥ = k 2 0 (ɛ⊥E⊥ + ɛ Ez ˆz +jguz × E⊥) (63)<br />
uguagliando le componenti omonime si ottiene Ez =0e:<br />
⎧<br />
⎪⎨ (k<br />
⎪⎩<br />
2 0ɛ⊥ − β 2 )Ex − j gk 2 0Ey =0<br />
j gk 2 0Ex +(k 2 0ɛ⊥ − β 2 )Ey =0<br />
Il sistema omogeneo (64) ammette soluzione diversa da quella banale solo se ha determinante<br />
nullo. Annullando il determinante si ha:<br />
da cui:<br />
Si ottengono i due seguenti valori di β:<br />
(k 2 0ɛ⊥ − β 2 ) 2 = g 2 k 4 0<br />
±gk 2 0 = k 2 0ɛ⊥ − β 2<br />
(64)<br />
(65)<br />
(66)<br />
√<br />
β1,2 = k0 ɛ⊥ ∓ g (67)<br />
che sostituiti in (64) permettono di ricavare il legame tra le componenti del vettore E. Nel<br />
caso β1<br />
√<br />
= k0 ɛ⊥ − g si ottiene Ey = −j Ex, mentre nel caso β2<br />
√<br />
= k0 ɛ⊥ + g il legame<br />
tra le componenti cartesiane del vettore campo elettrico sarà Ey =jEx. Si tratta di due<br />
polarizzazioni circolari sinistra e destra rispettivamente, poiché siè supposto che il verso di
Decomposizione di un vettore rispetto ad un’altro 15<br />
propagazione dell’onda fosse quello delle z positive. In definitiva si ottengono le due seguenti<br />
possibili forme del campo elettrico:<br />
−j βz<br />
E1 = A( ˆx − j ˆy)e<br />
−j βz<br />
E2 = A( ˆx +j ˆy)e<br />
(detta onda ciclotronica) (68a)<br />
(detta onda anticiclotronica) (68b)<br />
dove A e B sono due costanti arbitrarie. Se β1 e β2 sono reali le onde si propagano. Si può<br />
procedere in modo analogo per onde che si propagano nel verso delle z negative: in questo<br />
polarizzazioni levogire diventeranno destrogire e viceversa quelle destrogire diventeranno levo-<br />
gire. Le onde ciclotroniche (anticiclotroniche) prendono questo nome per il fatto che il verso<br />
di rotazione è coincidente (opposto) a quello di un elettrone che compie il moto ciclotronico<br />
intorno al campo magnetostatico.<br />
Decomposizione di un vettore rispetto ad un’altro<br />
A volte risulta utile poter scrivere un vettore complesso f come somma di due vettori, uno<br />
parallelo ad un vettore noto g = 0 e l’altro perpendicolare a g ∗ . A questo scopo basta<br />
sviluppare il prodotto<br />
g × (f × g ∗ )=f(g · g ∗ ) − g ∗ (g · f). (69)<br />
Dividendo ambo i membri per g · g ∗ è possibile esprimere f in funzione di g:<br />
∗ g · f<br />
f = g<br />
g · g∗ + g × (f × g∗ )<br />
g · g∗ Si noti che il primo addendo del secondo membro è parallelo a g ∗ , mentre il secondo addendo<br />
è perpendicolare a g. Questa decomposizione trova applicazione nella teoria delle antenne: se<br />
un’antenna riceve un campo elettrico E, il segnale ricevuto risulta essere proporzionale alla<br />
quantità:<br />
|h · E|2<br />
p(h, E) =<br />
|h| 2 |h × E|<br />
=1−<br />
|E| 2 |h| 2 |E| 2<br />
(71)<br />
essendo h un parametro caratteristico dell’antenna (vettore altezza efficace). Dunque un’an-<br />
tenna riceve solo la parte parallela alla propria altezza efficace.<br />
(70)