Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
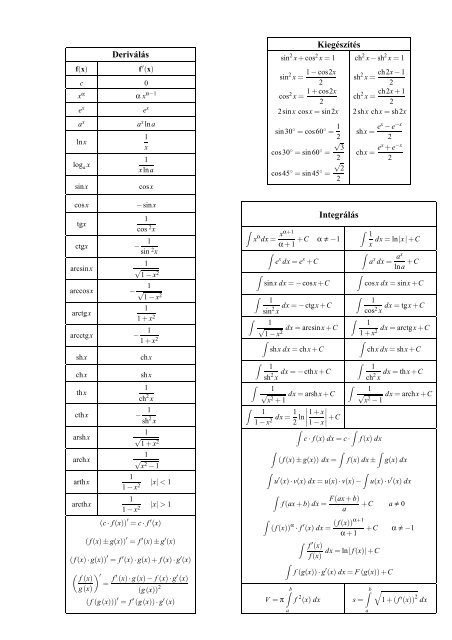
<strong>Deriválás</strong><br />
f(x) f ′ (x)<br />
c 0<br />
x α α x α−1<br />
e x e x<br />
a x a x lna<br />
lnx<br />
log a x<br />
1<br />
x<br />
1<br />
xlna<br />
sinx cosx<br />
cosx −sinx<br />
tgx<br />
1<br />
cos 2 x<br />
ctgx − 1<br />
sin 2 x<br />
arcsinx<br />
arccosx −<br />
arctgx<br />
1<br />
√ 1 − x 2<br />
1<br />
√ 1 − x 2<br />
1<br />
1+x 2<br />
arcctgx − 1<br />
1+x 2<br />
shx chx<br />
chx shx<br />
thx<br />
1<br />
ch 2 x<br />
cthx − 1<br />
sh 2 x<br />
arshx<br />
archx<br />
arthx<br />
arcthx<br />
1<br />
1 − x 2<br />
1<br />
1 − x 2<br />
1<br />
√ 1+x 2<br />
1<br />
√ x 2 − 1<br />
|x| < 1<br />
|x| > 1<br />
(c · f(x)) ′ = c · f ′ (x)<br />
( f(x) ± g(x)) ′ = f ′ (x) ± g ′ (x)<br />
( f(x) · g(x)) ′ = f ′ (x) · g(x)+ f(x) · g ′ (x)<br />
′<br />
f (x)<br />
=<br />
g(x)<br />
f ′ (x) · g(x) − f (x) · g ′ (x)<br />
(g(x)) 2<br />
( f (g(x))) ′ = f ′ (g(x)) · g ′ (x)<br />
<br />
<br />
<strong>Kiegészítés</strong><br />
sin 2 x+cos 2 x = 1 ch 2 x − sh 2 x = 1<br />
sin2 1 − cos2x<br />
x =<br />
2<br />
cos2 x = 1+cos2x<br />
2<br />
sh2 ch2x − 1<br />
x =<br />
2<br />
ch2 x = ch2x+1<br />
2<br />
2sinx cosx = sin2x 2shx chx = sh2x<br />
sin30◦ = cos60◦ = 1<br />
2<br />
cos30◦ = sin60◦ √<br />
3<br />
=<br />
2<br />
cos45◦ = sin45◦ √<br />
2<br />
=<br />
2<br />
<strong>Integrálás</strong><br />
x α dx = xα+1<br />
+C α−1<br />
α+1<br />
<br />
e x dx = e x +C<br />
<br />
<br />
<br />
sinx dx = −cosx+C<br />
1<br />
sin2 dx = −ctgx+C<br />
x<br />
1<br />
√ dx = arcsinx+C<br />
1 − x2 <br />
<br />
shx dx = chx+C<br />
1<br />
sh2 dx = −cthx+C<br />
x<br />
1<br />
√ x 2 + 1 dx = arshx+C<br />
<br />
1 1<br />
dx =<br />
1 − x2 2 ln<br />
<br />
<br />
<br />
1+x <br />
<br />
1<br />
− x<br />
+C<br />
<br />
<br />
c · f(x) dx = c ·<br />
<br />
<br />
<br />
<br />
( f(x) ± g(x)) dx =<br />
<br />
<br />
shx = ex − e−x 2<br />
chx = ex + e−x 2<br />
<br />
1<br />
dx = ln|x|+C<br />
x<br />
<br />
a x dx = ax<br />
lna +C<br />
<br />
cosx dx = sinx+C<br />
<br />
1<br />
cos2 dx = tgx+C<br />
x<br />
1<br />
dx = arctgx+C<br />
1+x 2<br />
<br />
chx dx = shx+C<br />
<br />
1<br />
ch2 dx = thx+C<br />
x<br />
1<br />
√ x 2 − 1 dx = archx+C<br />
f(x) dx<br />
<br />
f(x) dx ±<br />
u ′ <br />
(x) · v(x) dx = u(x) · v(x) −<br />
<br />
g(x) dx<br />
u(x) · v ′ (x) dx<br />
f(ax+b) dx = F(ax+b)<br />
+C a0<br />
a<br />
( f(x)) α · f ′ (x) dx =<br />
V = π<br />
<br />
b<br />
a<br />
f ′ (x)<br />
f(x)<br />
( f(x))α+1<br />
α+1<br />
dx = ln| f(x)|+C<br />
+C α−1<br />
f (g(x)) · g ′ (x) dx = F (g(x))+C<br />
f 2 (x) dx s =<br />
b<br />
a<br />
<br />
1+( f ′ (x)) 2 dx
Laplace-transzformáció<br />
f(t) f(s)<br />
e at<br />
c<br />
sinat<br />
cosat<br />
shat<br />
chat<br />
t n<br />
1<br />
s − a<br />
c<br />
s<br />
a<br />
s2 + a2 s<br />
s2 + a2 a<br />
s2 − a2 s<br />
s2 − a2 n!<br />
s n+1<br />
e at · f(t) f(s − a)<br />
t n · f(t) (−1) n · f (n) (s)<br />
f ′ (t) s · f(s) − f(0)<br />
y ′ s · y − y(0)<br />
f ′′ (t) s 2 · f(s) − s · f(0) − f ′ (0)<br />
y ′′ s 2 · y − s · y(0) − y ′ (0)<br />
f(t − a) e −sa · f(s)<br />
Valószínűségszámítás<br />
Binomiális eloszlás: P(ξ=k) = n k · pk ·(1 − p) n−k k = 0,1,2,...,n<br />
Hipergeometrikus eloszlás: P(ξ=k) =<br />
s<br />
k<br />
N−s · n−k<br />
k = 0,1,2,...,n<br />
Poisson-eloszlás: P(ξ=k) = λk<br />
k! · e−λ k = 0,1,2,...<br />
⎧<br />
⎪⎨<br />
1<br />
Egyenletes eloszlás: f(x) = b − a<br />
⎪⎩<br />
0<br />
ha a < x < b<br />
egyébként<br />
<br />
λ · e−λx Exponenciális eloszlás: f(x) =<br />
0<br />
ha 0 < x<br />
egyébként<br />
1<br />
Normális eloszlás: f(x) =<br />
σ · √ − m)2<br />
· e−(x 2σ<br />
2π 2<br />
x ∈R<br />
M(ξ) = ∑xi pi<br />
i<br />
D 2 (ξ) = ∑x i<br />
2 i pi<br />
2 M(ξ) =<br />
− ∑xi pi<br />
i<br />
∞<br />
x · f(x) dx D<br />
−∞<br />
2 (ξ) = ∞<br />
x<br />
−∞<br />
2 <br />
∞<br />
2<br />
· f(x) dx − x · f(x) dx<br />
−∞<br />
N<br />
n<br />
Matematikai statisztika<br />
Empirikus várható érték (mintaközép)<br />
ξ = ξ1 + ξ2 +...+ ξn<br />
<br />
n<br />
<br />
M ξ = m D ξ = σ √<br />
n<br />
Empirikus szórásnégyzet<br />
S 2 n =<br />
n<br />
∑<br />
i=1<br />
<br />
ξi − ξ<br />
n<br />
2<br />
M S2 n − 1<br />
n =<br />
n σ2<br />
Korrigált empirikus szórásnégyzet<br />
S ∗ n 2 =<br />
n<br />
∑<br />
i=1<br />
<br />
ξi − ξ<br />
n − 1<br />
M S ∗ n 2 = σ 2<br />
Konfidenciaintervallum normális eloszlás várható értékére<br />
((1 − ε) szintű)<br />
<br />
σ σ<br />
<br />
ξ − uε √ , ξ+uε √ ahol<br />
n n<br />
<br />
<br />
ξ − m √<br />
P −uε < n < uε = 2Φ(uε) − 1 = 1 − ε<br />
σ<br />
2<br />
u-próba valószínűségi változója<br />
u =<br />
ξ − m<br />
σ<br />
√ n<br />
t-próba valószínűségi változója<br />
t =<br />
ξ − m<br />
S ∗ n<br />
√ n