Méthodes numériques pour des systèmes hyperboliques avec terme ...

CHAPITRE 3. ÉTUDE DES MODÈLES M 1
10
9
’./Riemann.txt’ u 1:2
’./Godunov.txt’ u 1:2
’./HLL.txt’ u 1:2
0.5
0
’./Riemann.txt’ u 1:3
’./Godunov.txt’ u 1:3
’./HLL.txt’ u 1:3
8
-0.5
7
6
-1
5
-1.5
4
-2
3
2
-2.5
1
-1 -0.5 0 0.5 1
-3
-1 -0.5 0 0.5 1
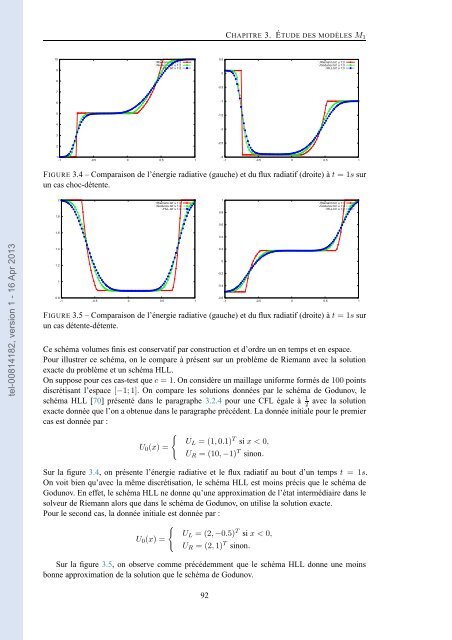
FIGURE 3.4 – Comparaison de l’énergie radiative (gauche) et du flux radiatif (droite) àt = 1s sur
un cas choc-détente.
2
1.8
’./Riemann.txt’ u 1:2
’./Godunov.txt’ u 1:2
’./HLL.txt’ u 1:2
1
0.8
’./Riemann.txt’ u 1:3
’./Godunov.txt’ u 1:3
’./HLL.txt’ u 1:3
0.6
1.6
0.4
tel-00814182, version 1 - 16 Apr 2013
1.4
1.2
1
0.8
-1 -0.5 0 0.5 1
0.2
0
-0.2
-0.4
-0.6
-1 -0.5 0 0.5 1
FIGURE 3.5 – Comparaison de l’énergie radiative (gauche) et du flux radiatif (droite) àt = 1s sur
un cas détente-détente.
Ce schéma volumes finis est conservatif par construction et d’ordre un en temps et en espace.
Pour illustrer ce schéma, on le compare à présent sur un problème de Riemann avec la solution
exacte du problème et un schéma HLL.
On suppose pour ces cas-test quec = 1. On considère un maillage uniforme formés de100 points
discrétisant l’espace [−1;1]. On compare les solutions données par le schéma de Godunov, le
schéma HLL [70] présenté dans le paragraphe 3.2.4 pour une CFL égale à 1 2
avec la solution
exacte donnée que l’on a obtenue dans le paragraphe précédent. La donnée initiale pour le premier
cas est donnée par :
{
U L = (1,0.1) T si x < 0,
U 0 (x) =
U R = (10,−1) T sinon.
Sur la figure 3.4, on présente l’énergie radiative et le flux radiatif au bout d’un temps t = 1s.
On voit bien qu’avec la même discrétisation, le schéma HLL est moins précis que le schéma de
Godunov. En effet, le schéma HLL ne donne qu’une approximation de l’état intermédiaire dans le
solveur de Riemann alors que dans le schéma de Godunov, on utilise la solution exacte.
Pour le second cas, la donnée initiale est donnée par :
{
U L = (2,−0.5) T si x < 0,
U 0 (x) =
U R = (2,1) T sinon.
Sur la figure 3.5, on observe comme précédemment que le schéma HLL donne une moins
bonne approximation de la solution que le schéma de Godunov.
92