Méthodes numériques pour des systèmes hyperboliques avec terme ...

CHAPITRE 5. RÉSULTATS NUMÉRIQUES
0.5
0.4
exact solution
k=3
0.3
k=2
k=1
0.2
k=0
0.1
0
−0.1
−0.2
−0.3
−0.4
−0.5
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
tel-00814182, version 1 - 16 Apr 2013
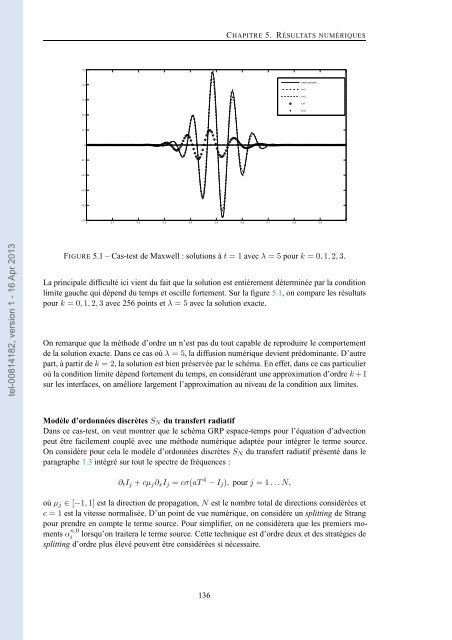
FIGURE 5.1 – Cas-test de Maxwell : solutions àt = 1 avec λ = 5 pour k = 0,1,2,3.
La principale difficulté ici vient du fait que la solution est entièrement déterminée par la condition
limite gauche qui dépend du temps et oscille fortement. Sur la figure 5.1, on compare les résultats
pour k = 0,1,2,3 avec 256 points et λ = 5 avec la solution exacte.
On remarque que la méthode d’ordre un n’est pas du tout capable de reproduire le comportement
de la solution exacte. Dans ce cas oùλ = 5, la diffusion numérique devient prédominante. D’autre
part, à partir dek = 2, la solution est bien préservée par le schéma. En effet, dans ce cas particulier
où la condition limite dépend fortement du temps, en considérant une approximation d’ordre k+1
sur les interfaces, on améliore largement l’approximation au niveau de la condition aux limites.
Modèle d’ordonnées discrètes S N du transfert radiatif
Dans ce cas-test, on veut montrer que le schéma GRP espace-temps pour l’équation d’advection
peut être facilement couplé avec une méthode numérique adaptée pour intégrer le terme source.
On considère pour cela le modèle d’ordonnées discrètes S N du transfert radiatif présenté dans le
paragraphe 1.3 intégré sur tout le spectre de fréquences :
∂ t I j +cµ j ∂ x I j = cσ(aT 4 −I j ), pour j = 1...N,
où µ j ∈ [−1,1] est la direction de propagation, N est le nombre total de directions considérées et
c = 1 est la vitesse normalisée. D’un point de vue numérique, on considère un splitting de Strang
pour prendre en compte le terme source. Pour simplifier, on ne considèrera que les premiers momentsα
n,0
i
lorsqu’on traitera le terme source. Cette technique est d’ordre deux et des stratégies de
splitting d’ordre plus élevé peuvent être considérées si nécessaire.
136