Les chiffres significatifs

Les chiffres significatifs
Les chiffres mesurés sont les seuls chiffres qui valent la peine d'être utilisés et publiés. Ce sont
les seuls chiffres qui veulent vraiment dire quelque chose. Ce sont les seuls chiffres importants.
Ce sont les chiffres significatifs.
Si vous donnez des chiffres non mesurés dans vos rapports, alors pourquoi aller au laboratoire?
Autant rester chez soi bien affalé devant la télé et les inventer là.
Les chiffres significatifs sont les chiffres certains et le premier chiffre incertain.
Les chiffres certains sont toujours donnés par l'appareil, tandis que le premier chiffre incertain doit
être évalué, apprécié, voire deviné par l'expérimentateur.
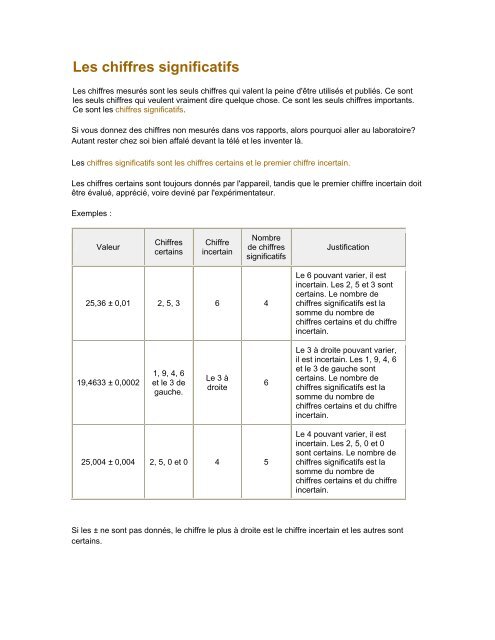
Exemples :
Valeur
Chiffres
certains
Chiffre
incertain
Nombre
de chiffres
significatifs
25,36 ± 0,01 2, 5, 3 6 4
19,4633 ± 0,0002
1, 9, 4, 6
et le 3 de
gauche.
Le 3 à
droite
25,004 ± 0,004 2, 5, 0 et 0 4 5
6
Justification
Le 6 pouvant varier, il est
incertain. Les 2, 5 et 3 sont
certains. Le nombre de
chiffres significatifs est la
somme du nombre de
chiffres certains et du chiffre
incertain.
Le 3 à droite pouvant varier,
il est incertain. Les 1, 9, 4, 6
et le 3 de gauche sont
certains. Le nombre de
chiffres significatifs est la
somme du nombre de
chiffres certains et du chiffre
incertain.
Le 4 pouvant varier, il est
incertain. Les 2, 5, 0 et 0
sont certains. Le nombre de
chiffres significatifs est la
somme du nombre de
chiffres certains et du chiffre
incertain.
Si les ± ne sont pas donnés, le chiffre le plus à droite est le chiffre incertain et les autres sont
certains.

Avantages
Le principal avantage apparaît lorsque vous faites des opérations arithmétiques avec des
mesures imprécises. Ainsi :
• 25,6 * 25,6 = 655 avec la méthode des chiffres significatifs (vous donnez le même
nombre de chiffres au produit que le terme qui en a le moins. Dans ce cas, vous donnez
trois chiffres significatifs).
• (25,6 ± 0,1) * (25,6 ± 0,1) = 655 ± 5. Avec la méthode habituelle, ce n'est pas facile de
voir comment vous êtes arrivé à ± 5. Nous y reviendrons dans les sections Méthodes des
extrêmes et Méthode des sommes.
Inconvénients
Qui dit simplification dit approximation. Soient les valeurs suivantes :
• 24,6 ± 0,01
• 24,6 ± 0,02
• 24,6 ± 0,03
Avec les ±, vous voyez très bien que la première valeur a été mesurée avec plus de précision.
Par contre, avec les chiffres significatifs, vous écrivez, dans les trois cas, 24,6. Vous savez qu'il y
a trois chiffres significatifs et que le chiffre 6 est incertain, mais sans plus.
Voici un autre exemple d'inconvénient :
Supposons que vous vouliez connaître la précision de la mesure sur la quantité 2000. Si on ne
vous indique pas le ±, vous pouvez penser :
2000 ± 1 2000 ± 2 2000 ± 4 2000 ± 5 2000 ± 10 2000 ± 20
2000 ± 50 2000 ± 100 2000 ± 200 2000 ± 500 2000 ± 1000 2000 ± 2000
Vous ne savez donc rien de la précision de cette mesure. Il existe un moyen de connaître la
précision dans ce cas précis : il suffit de donner la mesure en exposant de 10, c'est-à-dire
d'utiliser la notation scientifique.
2,000 * 10 3 ou 2,00 * 10 3 ou 2,0 * 10 3 ou 2* 10 3
Il suffit d'écrire le 2 avec le bon nombre de chiffres significatifs. Dans cet exemple, 2,000 * 10 3
inclut les cas 2000 ± 1, 2000 ± 2, 2000 ± 4 et 2000 ± 5.

Cas des zéros
S'il y a des zéros dans la mesure, il faut les traiter de façon particulière. Leur position dans la
valeur de la mesure est très importante.
Par exemple :
2,000 a 4 chiffres significatifs, tandis que
0,002 n'a qu'un chiffre significatif.
La règle est simple, mais il faut la connaître et surtout ne pas oublier de l'appliquer.
Règle : Les zéros à l'extrême gauche ne sont pas significatifs; ils ne sont là que pour donner
l'ordre de grandeur du nombre.
Exemples :
Mesure
Résumé
Nombre de chiffres
significatifs
Justification
0,0001 1 Les zéros de gauche ne comptent pas.
1,0000 5 Les zéros de droite comptent.
0,1000 4 Le zéro de gauche ne compte pas.
0,0100 3 Les 2 zéros de gauche ne comptent pas.
000001 1 Les zéros de gauche ne comptent pas.
1,0001 5 Tous les zéros comptent.
Les chiffres certains sont les chiffres qui ne varient pas lorsque la mesure est répétée.
Le chiffre incertain est le dernier chiffre à droite. C'est le chiffre qui varie si la mesure est répétée.
Les chiffres significatifs sont les chiffres certains et le premier chiffre incertain.
L'utilisation des chiffres significatifs présente des avantages pour effectuer des opérations
mathématiques avec des mesures imprécises, et aussi des inconvénients, lorsque rien n'indique
la précision d'une mesure.
Les zéros de gauche ne sont pas significatifs; ils ne sont là que pour donner l'ordre de grandeur
de la mesure.
Tous les chiffres sont significatifs dans les valeurs publiées, les valeurs obtenues par comptage et
les définitions.

Incertitude absolue ou relative
Dans les sections précédentes, vous avez appris à faire des observations qualitatives, à prendre
des mesures, à reconnaître les problèmes liés aux mesures et à voir la nuance entre précision et
exactitude. Dans cette section, vous apprendrez à estimer l'erreur ou l'incertitude qui existe sur
une mesure.
Une mesure ne donne jamais la valeur exacte d'une propriété ou d'une grandeur à cause de tous
les problèmes rencontrés au moment de la mesure. La valeur peut être très proche de la valeur
réelle ou en être plus ou moins éloignée.
Incertitude absolue
Puisqu'il y a toujours un écart (si petit soit-il) entre la valeur mesurée et la valeur vraie, nous ne
sommes jamais sûrs de notre valeur mesurée. Il y a donc une incertitude. Cette incertitude
dépend de l'appareil de mesure, de la méthode suivie et de l'expérimentateur.
Mais quelle est la grandeur, l'importance, l'ampleur de cette incertitude? Nous sommes intéressés
à la quantifier, à la chiffrer pour être capable de nuancer et d'apprécier à sa juste valeur la mesure
obtenue.
Afin de comprendre comment évaluer l'incertitude, utilisons un exemple simple.
Vous voulez mesurer la longueur d'un crayon et vous devez évaluer l'incertitude
maximale de cette mesure. Pour cela, examinez en détail la règle utilisée, de même que
la méthode suivie.
Pour mesurer la longueur du crayon, vous placez la règle près du crayon en prenant soin
de vous assurer qu'un des bouts de la règle soit parfaitement aligné avec l'un des bouts
du crayon. En observant la règle, vous vous apercevez que ses bouts sont légèrement
arrondis par l'usure, ce qui rend difficile l'ajustement de la règle sur le bout du crayon. En
plus, l'autre bout du crayon n'arrive pas exactement vis-à-vis de l'une des graduations.
Vous pouvez être certain que la vraie valeur de la longueur est entre la graduation de la
règle tout juste avant le bout du crayon et la graduation tout juste après le bout du crayon.
Donc la vraie valeur est entre 5,7 et 5,8 cm.
Les scientifiques, d'un commun accord, ont établi par convention que l'incertitude maximale due à
un instrument de mesure est égale à la moitié de la plus petite graduation de l'instrument.
En l'occurrence, dans le cas qui nous occupe, celui de l'incertitude maximale, l'incertitude absolue
est 0,05 cm puisque la plus petite graduation est 0,1 cm (5,8 - 5,7).
Il y a donc lieu d'affirmer que le crayon mesure probablement 5,75 cm, qu'il pourrait mesurer
aussi peu que 5,70 cm et autant que 5,80 cm.
Par convention, vous écrivez alors 5,75 ± 0,05 cm. C'est plus court.
L'erreur annoncée est l'erreur de l'instrument de mesure.
Attention! La phrase précédente est extrêmement importante. Nous n'avons tenu compte que de

l'erreur de graduation de l'instrument, de l'erreur fortuite. Nous supposons qu'il n'y a pas d'erreur
systématique, que l'expérimentateur sait mesurer et que la bonne méthode de mesure a été
utilisée. Nous ferons toujours cette hypothèse
Incertitude relative
Une autre façon de donner l'incertitude consiste à la donner en pourcentage. C'est l'incertitude
relative.
Reprenons l'exemple de la mesure du crayon, dans lequel nous avons lu 5,75 ± 0,05 cm.
Nous pouvons écrire cette lecture en pourcentage de la façon suivante :
Incertitude relative =
incertitudeabsolue * 100
valeurmesurée
Exemple : incertitude relative = 0,05 * 100 =
5,75
La valeur mesurée étant 5,75, nous écrivons donc 5,75 cm ± 0,9 %.
Résumé
En général, l'incertitude maximale due à un instrument de mesure est égale à la moitié de la plus
petite graduation de l'instrument. Elle est égale au plus petit chiffre affiché pour les instruments à
affichage numérique.
Il y a deux façons de donner ce chiffre : l'incertitude absolue et l'incertitude relative.

Calculs et chiffres significatifs
Après avoir pris des mesures, il faut presque toujours faire des opérations arithmétiques comme
la multiplication, la division, l'addition et la soustraction.
Quand des mesures sont utilisées dans des calculs, il convient aussi de donner la précision du
résultat obtenu à partir des calculs.
Faut-il conserver tous les chiffres donnés par la calculatrice? Bien sûr que non
Puisque les mesures utilisées dans les calculs sont imprécises, le résultat du calcul est lui aussi
imprécis.
Les scientifiques utilisent des règles pour déterminer la précision d'un résultat. La preuve du bienfondé
de ces règles sera donnée plus tard.
Addition et soustraction
Le résultat d'une addition ou d'une soustraction a autant de décimales qu'en a la mesure la moins
précise utilisée dans le calcul.
Exemple 1 :
Vous voulez additionner les 3 mesures suivantes :
15,31 + 17,1 + 1,013
La calculatrice donne 33,423. C'est pourtant faux. Vous n'avez pas cette précision, car 15,31 a 2
décimales, 17,1 a une décimale et 1,013 en a 3. Il ne faut donc donner qu'une décimale, étant
donné que la mesure qui en a le moins en a seulement une.
Donc la réponse est 33,4 après avoir arrondi.
Exemple 2 :
Vous voulez soustraire les deux mesures suivantes :
33,62 - 4,1
La calculatrice affiche 29,52 comme réponse. C'est pourtant faux. Vous n'avez pas cette
précision, car 33,62 a 2 décimales et 4,1 n'en a qu'une. La réponse ne doit donc avoir qu'une
décimale.
La réponse est 29,5 après avoir arrondi

Multiplication et division
Le résultat d'une multiplication ou d'une division a autant de chiffres significatifs qu'en a la mesure
la moins précise utilisée dans le calcul
Exemple :
Soit 123,45 * 1,23
La calculatrice vous donnera 151,8435, ce qui n'a pas vraiment de sens. C'est comme si vous me
disiez que vous pesez 75,365243 kg. Nous savons pertinemment bien que vous n'avez pas de
pèse-personne aussi précis chez vous.
.
Nombre de chiffres
significatifs
Première mesure : 123,45 5
Seconde mesure : 1,23 3
Produit :
123,45 * 1,23 = 152
Voici un autre exemple :
Soit 154,2 / 23,045
.
3
Nombre de chiffres
significatifs
Première mesure : 154,2 4
Seconde mesure : 23,045 5
Quotient :
154,2 / 23,045 = 6,691
4
Justification
4 chiffres certains et un
chiffre incertain
2 chiffres certains et un
chiffre incertain
Le produit a autant de
chiffres significatifs que la
mesure qui en a le moins.
Justification
3 chiffres certains et un
chiffre incertain
4 chiffres certains et un
chiffre incertain
Le quotient a autant de
chiffres significatifs que la
mesure qui en a le moins.

Expressions arithmétiques
Quand vous rencontrez une expression arithmétique moins simple, comment tenir compte des
chiffres significatifs?
Voici un exemple un peu plus complexe :
100,5 + 2,1 (30,6 - 27,33)
20,0
Il est préférable de traiter l'exemple partie par partie.
Partie du calcul à
faire
A = (30,6 - 27,33)
B = 2,1 * A
C = 100,5 + B
D = C/20,0
Finalement
Action Raison
Il faut garder 2
chiffres.
Il faut garder 2
chiffres.
Il faut
conserver 4
chiffres.
Il faut
conserver 3
chiffres.
Il faut arrondir
la réponse
donnée par la
calculatrice.
Dans une soustraction, il
faut conserver autant de
décimales que le nombre
qui en contient le moins.
Or, 30,6 n'a qu'une
décimale.
Dans une multiplication,
il faut conserver autant
de chiffres que le
nombre qui en a le
moins. Or, les deux
nombres à multiplier ont
2 chiffres chacun.
La valeur B et 100,5 ont
une décimale. Dans une
addition, il faut conserver
autant de décimales que
le chiffre qui en a le
moins.
Dans une division, il faut
conserver autant de
chiffres que le nombre
qui en a le moins. La
valeur C a 4 chiffres
significatifs, tandis que
20,0 en a 3.
La calculatrice affiche
5,36835. Il faut arrondir à
3 chiffres significatifs.
Réponse
intermédiaire à titre
indicatif seulement
A = 3,27 (3,3 si on
arrondit à 2 chiffres
significatifs)
B = 6,867 (6,9 si on
arrondit à 2 chiffres
significatifs)
C =107,367 (107,4
si on arrondit à 4
chiffres significatifs)
D = 5,36835 (5,37 si
on arrondit à 3
chiffres significatifs)
La réponse finale
est donc 5,37

Cas des sinus
Le nombre de chiffres significatifs pour un sinus est égal à la somme des chiffres significatifs
et des décimales.
Exemples :
sin(89,31 degrés) = 0,999927 La mesure a 4 chiffres significatifs, dont 2
décimales. Le résultat a donc 6 chiffres
significatifs.
sin(30,1 degrés) = 0,5015 La mesure a 3 chiffres significatifs, dont une
décimale. Le résultat a donc 4 chiffres
significatifs.
Résumé
Le résultat d'une addition ou d'une soustraction a autant de décimales que la mesure qui en
a le moins.
Le résultat d'une multiplication ou d'une division a autant de chiffres significatifs que la
mesure qui en a le moins.
Il faut arrondir le résultat au bon nombre de chiffres significatifs une fois que le calcul
complet a été fait
Dans les calculs complexes, il ne faut pas arrondir les résultats intermédiaires, il ne faut
arrondir que le résultat final.
Le nombre de décimales dans la valeur du logarithme est égal au nombre de chiffres
significatifs dans la mesure.
Dans le cas des exposants de 10, le résultat a le même nombre de chiffres significatifs que
la mesure a de décimales.
Dans le cas des exponentielles, le nombre de chiffres significatifs du résultat est le même
que le nombre de chiffres significatifs de la mesure.
Le nombre de chiffres significatifs pour un sinus est égal à la somme des chiffres
significatifs et des décimales de la mesure.
.

Méthode des sommes d'incertitudes
Il existe plusieurs méthodes pour tenir compte des incertitudes des mesures. Nommons-en
quatre :
• la méthode des chiffres significatifs
• la méthodes des sommes d'incertitudes
• la méthodes des extrêmes
• la méthode du calcul différentiel
Dans cette section-ci, nous nous attardons à la méthode des sommes d'incertitudes.
La méthode utilise la notion d'incertitude absolue pour les calculs d'addition et de
soustraction et la notion d'incertitude relative pour les calculs de multiplication et de division.
Cas des additions et des soustractions
Règle : Pour les additions et les soustractions de mesures, il faut additionner les incertitudes
absolues.
Exemple d'addition de deux volumes : 10,00 ± 0,01 ml et 15,0 ± 0,2 ml.
• En additionnant,
25,00 ± 0,21 ml.
• En arrondissant,
25,0 ± 0,2 ml.
Exemple de soustraction de deux longueurs : 30,5 ± 0,5 cm et 20,1 ± 0,1 cm.
• En soustrayant,
10,4 ± 0,6 cm.
• En arrondissant, la réponse ne change pas :
10,4 ± 0,6 cm.

Cas des multiplications et des divisions
Règle : Pour les multiplications et les divisions, il faut additionner les incertitudes relatives.
Exemple de multiplication de deux longueurs : 10,5 ± 0,5 cm et 5,2 ± 0,2 cm.
ΔP = 0,5 + 0,2
P 10,5 5,2
où P est le produit des deux nombres et ΔP est l'incertitude sur le produit.
ΔP = 0,08608
P
Donc ΔP = P * 0,08608 = 10,5 * 5,2 * 0,08608 = 54,6 * 0,08608 = 4,70
En arrondissant, on obtient 55 ± 5 cm 2 .
Exemple de division d'une masse par un volume : 9,90 ± 0,01 g et 10,00 ± 0,02 ml
ΔQ = 0,01 + 0,02
Q 9,90 10,00
où Q est le quotient et ΔQ est l'incertitude sur le quotient.
ΔQ = 0,00301
Q
Donc ΔQ = Q * 0,00301 = (9,90/10,00) * 0,00301 = 0,990 * 0,00301 = 0,00298
En arrondissant, on obtient 0,990 ± 0,003 g/ml.