Contributions à l'étude de la classification spectrale et applications
Contributions à l'étude de la classification spectrale et applications
Contributions à l'étude de la classification spectrale et applications
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
74 C<strong>la</strong>ssification <strong>et</strong> éléments spectraux <strong>de</strong> <strong>la</strong> matrice affinité gaussienne<br />
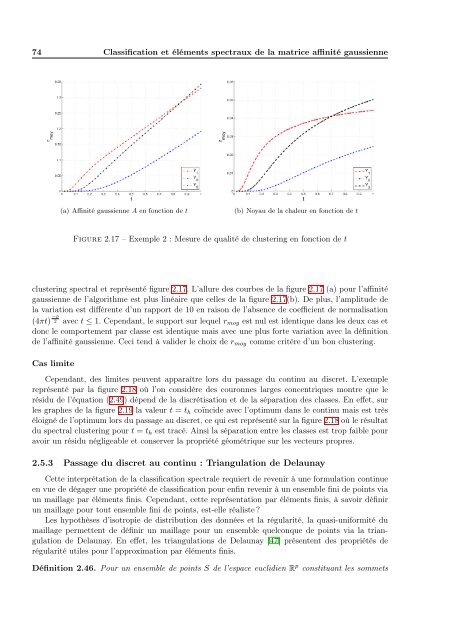
(a) Affinité gaussienne A en fonction <strong>de</strong> t (b) Noyau <strong>de</strong> <strong>la</strong> chaleur en fonction <strong>de</strong> t<br />
Figure 2.17 – Exemple 2 : Mesure <strong>de</strong> qualité <strong>de</strong> clustering en fonction <strong>de</strong> t<br />
clustering spectral <strong>et</strong> représenté figure 2.17. L’allure <strong>de</strong>s courbes <strong>de</strong> <strong>la</strong> figure 2.17 (a) pour l’affinité<br />
gaussienne <strong>de</strong> l’algorithme est plus linéaire que celles <strong>de</strong> <strong>la</strong> figure 2.17(b). De plus, l’amplitu<strong>de</strong> <strong>de</strong><br />
<strong>la</strong> variation est différente d’un rapport <strong>de</strong> 10 en raison <strong>de</strong> l’absence <strong>de</strong> coefficient <strong>de</strong> normalisation<br />
(4πt) −p<br />
2 avec t ≤ 1. Cependant, le support sur lequel rmoy est nul est i<strong>de</strong>ntique dans les <strong>de</strong>ux cas <strong>et</strong><br />
donc le comportement par c<strong>la</strong>sse est i<strong>de</strong>ntique mais avec une plus forte variation avec <strong>la</strong> définition<br />
<strong>de</strong> l’affinité gaussienne. Ceci tend <strong>à</strong> vali<strong>de</strong>r le choix <strong>de</strong> rmoy comme critère d’un bon clustering.<br />
Cas limite<br />
Cependant, <strong>de</strong>s limites peuvent apparaître lors du passage du continu au discr<strong>et</strong>. L’exemple<br />
représenté par <strong>la</strong> figure 2.18 où l’on considère <strong>de</strong>s couronnes <strong>la</strong>rges concentriques montre que le<br />
résidu <strong>de</strong> l’équation (2.49) dépend <strong>de</strong> <strong>la</strong> discrétisation <strong>et</strong> <strong>de</strong> <strong>la</strong> séparation <strong>de</strong>s c<strong>la</strong>sses. En eff<strong>et</strong>, sur<br />
les graphes <strong>de</strong> <strong>la</strong> figure 2.19 <strong>la</strong> valeur t = th coïnci<strong>de</strong> avec l’optimum dans le continu mais est très<br />
éloigné <strong>de</strong> l’optimum lors du passage au discr<strong>et</strong>, ce qui est représenté sur <strong>la</strong> figure 2.18 où le résultat<br />
du spectral clustering pour t = th est tracé. Ainsi <strong>la</strong> séparation entre les c<strong>la</strong>sses est trop faible pour<br />
avoir un résidu négligeable <strong>et</strong> conserver <strong>la</strong> propriété géométrique sur les vecteurs propres.<br />
2.5.3 Passage du discr<strong>et</strong> au continu : Triangu<strong>la</strong>tion <strong>de</strong> De<strong>la</strong>unay<br />
C<strong>et</strong>te interprétation <strong>de</strong> <strong>la</strong> c<strong>la</strong>ssification <strong>spectrale</strong> requiert <strong>de</strong> revenir <strong>à</strong> une formu<strong>la</strong>tion continue<br />
en vue <strong>de</strong> dégager une propriété <strong>de</strong> c<strong>la</strong>ssification pour enfin revenir <strong>à</strong> un ensemble fini <strong>de</strong> points via<br />
un mail<strong>la</strong>ge par éléments finis. Cependant, c<strong>et</strong>te représentation par éléments finis, <strong>à</strong> savoir définir<br />
un mail<strong>la</strong>ge pour tout ensemble fini <strong>de</strong> points, est-elle réaliste ?<br />
Les hypothèses d’isotropie <strong>de</strong> distribution <strong>de</strong>s données <strong>et</strong> <strong>la</strong> régu<strong>la</strong>rité, <strong>la</strong> quasi-uniformité du<br />
mail<strong>la</strong>ge perm<strong>et</strong>tent <strong>de</strong> définir un mail<strong>la</strong>ge pour un ensemble quelconque <strong>de</strong> points via <strong>la</strong> triangu<strong>la</strong>tion<br />
<strong>de</strong> De<strong>la</strong>unay. En eff<strong>et</strong>, les triangu<strong>la</strong>tions <strong>de</strong> De<strong>la</strong>unay [47] présentent <strong>de</strong>s propriétés <strong>de</strong><br />
régu<strong>la</strong>rité utiles pour l’approximation par éléments finis.<br />
Définition 2.46. Pour un ensemble <strong>de</strong> points S <strong>de</strong> l’espace euclidien R p constituant les somm<strong>et</strong>s