Cuadricas - unne

ANÁLISIS MATEMÁTICO IIBreve Repaso de Geometría en el PlanoCuádricasEcuación Lineal (todas las variables están elevadas a la 1ª) ⇒RectaEcuación General de la Recta:Ax + By + C = 0 y = f ( x)ybEcuación Segmentaria de la Recta:xa+ by= 1axEcuaciones Cuadráticas (por lo menos una variable elevada al cuadrado) ⇒CónicasCónicas con centro en el origen:2 2x y± ± = 12 2a bybLos términos positivos ⇒ Elipse2 2x+a2+yb2= 1axyrSi además a = b = r ⇒ Circunferencia2 2 2x + y = rrxUn término positivo y otro negativo ⇒ Hipérbolaxa22−by22= 1El término negativo determina el eje imaginario.La curva NO corta al eje imaginarioNo se pueden dar dos signos negativos. No se estaría en el plano real.yCónicas sin centro:y 2 = 2px ⇒ ParábolaLa parábola rodea al eje de la variable lineal.x1

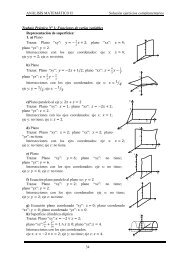
ANÁLISIS MATEMÁTICO IIDe acuerdo a los valores de los parámetros el hiperboloide de una hoja puedetomar distintas posiciones.CuádricasUn término cuadrático positivo y dos negativos: HIPERBOLOIDE DE DOS HOJASx−a22−yb22z+c22= 1El hiperboloide NO corta al plano formado por los ejes delas variables que están en los términos negativos.Trazas del hiperboloide de dos hojas:Traza con el plano “xy”, z = 02 2x y− − = 1 No existe traza.2 2abTraza con un plano paralelo al “xy”, z = d conComo22x y d− − +2 2a b c2dd > c , > 12c2 2x y+ = 12a b12122= 1xa22y+b22d >d=c. Entonces se puede llegar a:elipsec22− 16

ANÁLISIS MATEMÁTICO IICuádricasTraza con el plano “xz”, y = 02 2x−a2z+c2= 1hipérbola eje real en “z”, eje imaginario en “x”.c-cTraza con el plano “yz”, x = 02 2y−b2z+c2= 1hipérbola eje real en “z”, eje imaginario en “y”.c-cSi los dos parámetros negativos tienen el mismo valor el Hiperboloide de dos hojas sedice de revolución. (se llega a a 1 = b 1 )7

ANÁLISIS MATEMÁTICO IICuádricas sin centro:2 2x y2 z = ± ±p q⋅ PARABOLOIDESCuádricasLos dos términos cuadráticos con el mismo signo: PARABOLOIDE ELÍPTICO2x2 ⋅ z = +p2yqEl paraboloide rodea al eje de la variable linealTrazas del paraboloide elíptico:Traza con el plano “xy”, z = 02 2xp+ qy= 0Punto (0,0) vértice del paraboloide.Traza con un plano paralelo al “xy”, z = d con d > 02 2x y2 ⋅ d = +p qEntonces se puede llegar a:2 2x y+ = 1 elipse2 2p1q 1Traza con el plano “xz”, y = 022 ⋅ z =xpparábola que abraza al eje “z”.8

ANÁLISIS MATEMÁTICO IICuádricasTraza con el plano “yz”, x = 022 ⋅ z =yqparábola que abraza al eje “z”.Si la sección normal al eje al que rodea el paraboloide es una circunferencia, es decir p =q, el paraboloide se llama de revolución.Si el vértice está desplazado sobre el eje al que rodea el paraboloide, se tiene:2 2x y2 ⋅ z = + + kp qVariando los parámetros ya mencionados y sus signos se pueden tener los siguientesparaboloides:Los dos términos cuadráticos con distinto signo: PARABOLOIDE HIPERBÓLICO2x2 ⋅ z = − +p2yqZYX9

ANÁLISIS MATEMÁTICO IITrazas del paraboloide hiperbólico:CuádricasTraza con el plano “xy”, z = 02 2x−p⎛ x⎜−⎝ p21y+qy+q21= 0⎞ ⎛⎟ ⋅⎜+⎠ ⎝xp1 1 1 1Dos rectas que pasan por el origen.+yq⎞⎟ = 0⎠Traza con el plano “xz”, y = 02x2 ⋅ z = −pparábola que abraza al eje “z”,con ramas de concavidad negativas.Traza con el plano “yz”, x = 02y2 ⋅ z =q2parábola que abraza al eje “z”,con ramas de concavidad positivas.10

ANÁLISIS MATEMÁTICO IISi marcamos la intersección del paraboloide hiperbólico con planos paralelosal “xy” tenemos:z = ±d2 222x yx y2 ⋅ d = − +− + = 1p q2 ⋅ d ⋅ p 2 ⋅ d ⋅ qCuádricasQue dependiendo del signo de d son hipérbolas con eje imaginario x o y.El paraboloide hiperbólico es una superficie reglada.11

ANÁLISIS MATEMÁTICO IICuádricasSuperficies Cilíndricas:Se llama superficie cilíndrica a una superficie generada por una recta que se desplazaparalela a si misma siguiendo una curva C llamada directriz.ZOP(x,y,z)ZYCR(x,y,0)XYXSi la directriz de una superficie cilíndrica es una circunferencia, la superficie se llamacircular. Análogamente, tenemos superficies cilíndricas parabólicas, elípticas e hiperbólicas.12