Vol. 2
Vol. 2 Vol. 2
Fco. Fdez. Morales EXAMEN MODELO 35 Pág. 141Calculemos el determinante de esta matriz inversa.1D − =1 −2 10 1 − 2 = 10 0 1SOLUCIÓN EJERCICIO 4.-Al estar el centro de la circunferencia en el semieje positivo deabscisas, las coordenadas del mismo serán C = (a, 0), siendo a > 0.Como además la circunferencia pasa por el origen de coordenadas, elradio, r, de la misma coincide con el valor de la abscisa del centro, esdecir con a, por tanto r = a.La ecuación de la recta tangente en forma general es: y + x -1 = 0.Se verificará que la distancia de C a la recta tangente coincide con el radio y con a:dist (C, recta tangente) = a + 0 − 1⇒ a =2 21 + 1a − 12Si nos fijamos en los datos del problema y observamos la figura, deduciremos que laabscisa a del centro de la circunferencia, es mayor que cero pero también menor que 1, por lo quea-1 sería negativo; como tenemos que tomar el valor absoluto, escribiremos lo siguiente:aa = − ( − 1)1⇒ 2 a = 1− a ⇒ 2 a + a = 1 ⇒ ( 2 +1) a = 1 ⇒ a =21+ 22 − 12 − 1a =⇒ a = ⇒ a = 2 − 1 ⇒ r = 2 − 1( 2 +1) ( 2 − 1)2 − 1( )luego el centro tiene de coordenadas C = 2 − 1, 0 y el radio vale 2 − 1 .1CP1SOLUCIONES Opción BSOLUCIÓN EJERCICIO 1.-(a) Dibujemos el primer trozo, 5x + 10, para losvalores de x # -1. Se trata de una recta que pasa por lospuntos, (-2, 0) y (-1, 5). La gráfica es la situada al lado.Dibujemos el segundo trozo, x 2 -2x + 10, para losvalores de x > -1. Se trata de una parábola:abscisa del vértice = − b 22a=2= 1ordenada del vértice = 1 2 -2·1 + 2 = 1-351-2 -11 2 3
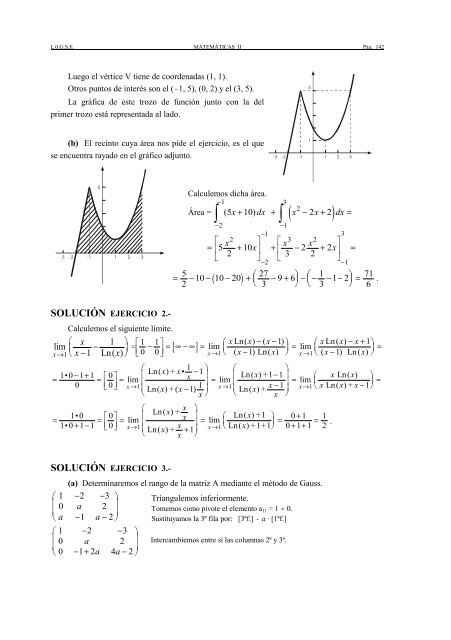
L.0.G.S.E. MATEMÁTICAS II Pág. 142Luego el vértice V tiene de coordenadas (1, 1).Otros puntos de interés son el (-1, 5), (0, 2) y el (3, 5).La gráfica de este trozo de función junto con la delprimer trozo está representada al lado.5(b) El recinto cuya área nos pide el ejercicio, es el quese encuentra rayado en el gráfico adjunto.-31-2 -11 2 3-35-2 -11 2 3Calculemos dicha área.−132( 5x + 10)dx + x − 2x + 2 dx =Área =∫ ∫ ( )−2−1−13⎡ 2 ⎤ ⎡ 3 2xx x ⎤= ⎢5 + 10x⎥ + ⎢ − 2 + 2x⎥ =⎣ 2⎦ ⎣3 2⎦−2−15= − − ( − ) +⎛− +.⎝⎜ ⎞⎠⎟ − ⎛⎜⎝− − − ⎞2 10 10 20 2719 633 1 2 ⎠⎟ = 716SOLUCIÓN EJERCICIO 2.-Calculemos el siguiente límite.⎛ xlim=x→ x − − 1 ⎞ ⎡ 1 111⎜⎟ −⎤[ ]1 ⎝ 1 Ln( x)⎠ ⎣⎢ 0 0 ⎦⎥ = ∞ − ∞ = ⎛ x Ln( x) − ( x − ) ⎞ ⎛ x Ln( x)− x + ⎞lim ⎜⎟ = lim ⎜⎟ =x→1 ⎝ ( x − 1) Ln( x)⎠ x→1⎝ ( x − 1) Ln( x)⎠⎛1− +==⎡ ⎤⎣⎢ ⎦⎥ =−⎞ ⎛⎞1•0 1 1 0 ⎜1 ⎟ ⎜ − 1 ⎟ ⎛⎞lim Ln( x ) + x• xLn( x) +1x Ln( x)=⎜⎝− ⎟ ⎜ −= ⎜⎟ =0 0 →1 → ⎟ →1 1 lim limx x 1 1 x 1Ln( x) + ( x )⎝− ⎠⎠ ⎝Ln( x) +xx Ln( x) + x 1xx ⎠=+ − = ⎡ ⎛⎞1•0 0⎣ ⎢ ⎤⎦⎥ = ⎜ Ln( x) +x⎟ ⎛ 1 ⎞ 0 + 1= ⎜⎟ =1 0 1 1 0 ⎜⎝+ ⎟ ⎝⎠ + + = 1limxLn( x) +lim•x→1 x→1Ln( x) +x1Ln( x) +1+ 1 0 1 1 2x ⎠.SOLUCIÓN EJERCICIO 3.-(a) Determinaremos el rango de la matriz A mediante el método de Gauss.⎛ 1 −2 −3⎞ Triangulemos inferiormente.⎜ 0 a 2 ⎟Tomemos como pivote el elemento a 11 = 1 … 0.⎜⎟⎝ a −1 a − 2 ⎠ Sustituyamos la 3ª fila por: [3ªf.] - a · [1ªf.]⎛ 1 −2 −3⎞⎜ 0 a 2 ⎟ Intercambiemos entre sí las columnas 2ª y 3ª.⎜⎟⎝ 0 − 1+2a4a− 2 ⎠
- Page 43 and 44: L.0.G.S.E. MATEMÁTICAS II Pág. 70
- Page 45 and 46: L.0.G.S.E. MATEMÁTICAS II Pág. 72
- Page 47 and 48: L.0.G.S.E. MATEMÁTICAS II Pág. 74
- Page 49 and 50: L.0.G.S.E. MATEMÁTICAS II Pág. 76
- Page 51 and 52: L.0.G.S.E. MATEMÁTICAS II Pág. 78
- Page 53 and 54: L.0.G.S.E. MATEMÁTICAS II Pág. 10
- Page 55 and 56: L.0.G.S.E. MATEMÁTICAS II Pág. 10
- Page 57 and 58: L.0.G.S.E. MATEMÁTICAS II Pág. 10
- Page 59 and 60: L.0.G.S.E. MATEMÁTICAS II Pág. 10
- Page 61 and 62: L.0.G.S.E. MATEMÁTICAS II Pág. 10
- Page 63 and 64: L.0.G.S.E. MATEMÁTICAS II Pág. 11
- Page 65 and 66: L.0.G.S.E. MATEMÁTICAS II Pág. 11
- Page 67 and 68: L.0.G.S.E. MATEMÁTICAS II Pág. 11
- Page 69 and 70: L.0.G.S.E. MATEMÁTICAS II Pág. 11
- Page 71 and 72: L.0.G.S.E. MATEMÁTICAS II Pág. 11
- Page 73 and 74: L.0.G.S.E. MATEMÁTICAS II Pág. 12
- Page 75 and 76: L.0.G.S.E. MATEMÁTICAS II Pág. 12
- Page 77 and 78: L.0.G.S.E. MATEMÁTICAS II Pág. 12
- Page 79 and 80: L.0.G.S.E. MATEMÁTICAS II Pág. 12
- Page 81 and 82: L.0.G.S.E. MATEMÁTICAS II Pág. 12
- Page 83 and 84: L.0.G.S.E. MATEMÁTICAS II Pág. 13
- Page 85 and 86: L.0.G.S.E. MATEMÁTICAS II Pág. 13
- Page 87 and 88: L.0.G.S.E. MATEMÁTICAS II Pág. 13
- Page 89 and 90: L.0.G.S.E. MATEMÁTICAS II Pág. 13
- Page 91 and 92: L.0.G.S.E. MATEMÁTICAS II Pág. 13
- Page 93: L.0.G.S.E. MATEMÁTICAS II Pág. 14
- Page 97 and 98: L.0.G.S.E. MATEMÁTICAS II Pág. 14
L.0.G.S.E. MATEMÁTICAS II Pág. 142Luego el vértice V tiene de coordenadas (1, 1).Otros puntos de interés son el (-1, 5), (0, 2) y el (3, 5).La gráfica de este trozo de función junto con la delprimer trozo está representada al lado.5(b) El recinto cuya área nos pide el ejercicio, es el quese encuentra rayado en el gráfico adjunto.-31-2 -11 2 3-35-2 -11 2 3Calculemos dicha área.−132( 5x + 10)dx + x − 2x + 2 dx =Área =∫ ∫ ( )−2−1−13⎡ 2 ⎤ ⎡ 3 2xx x ⎤= ⎢5 + 10x⎥ + ⎢ − 2 + 2x⎥ =⎣ 2⎦ ⎣3 2⎦−2−15= − − ( − ) +⎛− +.⎝⎜ ⎞⎠⎟ − ⎛⎜⎝− − − ⎞2 10 10 20 2719 633 1 2 ⎠⎟ = 716SOLUCIÓN EJERCICIO 2.-Calculemos el siguiente límite.⎛ xlim=x→ x − − 1 ⎞ ⎡ 1 111⎜⎟ −⎤[ ]1 ⎝ 1 Ln( x)⎠ ⎣⎢ 0 0 ⎦⎥ = ∞ − ∞ = ⎛ x Ln( x) − ( x − ) ⎞ ⎛ x Ln( x)− x + ⎞lim ⎜⎟ = lim ⎜⎟ =x→1 ⎝ ( x − 1) Ln( x)⎠ x→1⎝ ( x − 1) Ln( x)⎠⎛1− +==⎡ ⎤⎣⎢ ⎦⎥ =−⎞ ⎛⎞1•0 1 1 0 ⎜1 ⎟ ⎜ − 1 ⎟ ⎛⎞lim Ln( x ) + x• xLn( x) +1x Ln( x)=⎜⎝− ⎟ ⎜ −= ⎜⎟ =0 0 →1 → ⎟ →1 1 lim limx x 1 1 x 1Ln( x) + ( x )⎝− ⎠⎠ ⎝Ln( x) +xx Ln( x) + x 1xx ⎠=+ − = ⎡ ⎛⎞1•0 0⎣ ⎢ ⎤⎦⎥ = ⎜ Ln( x) +x⎟ ⎛ 1 ⎞ 0 + 1= ⎜⎟ =1 0 1 1 0 ⎜⎝+ ⎟ ⎝⎠ + + = 1limxLn( x) +lim•x→1 x→1Ln( x) +x1Ln( x) +1+ 1 0 1 1 2x ⎠.SOLUCIÓN EJERCICIO 3.-(a) Determinaremos el rango de la matriz A mediante el método de Gauss.⎛ 1 −2 −3⎞ Triangulemos inferiormente.⎜ 0 a 2 ⎟Tomemos como pivote el elemento a 11 = 1 … 0.⎜⎟⎝ a −1 a − 2 ⎠ Sustituyamos la 3ª fila por: [3ªf.] - a · [1ªf.]⎛ 1 −2 −3⎞⎜ 0 a 2 ⎟ Intercambiemos entre sí las columnas 2ª y 3ª.⎜⎟⎝ 0 − 1+2a4a− 2 ⎠