FORMULARIO:

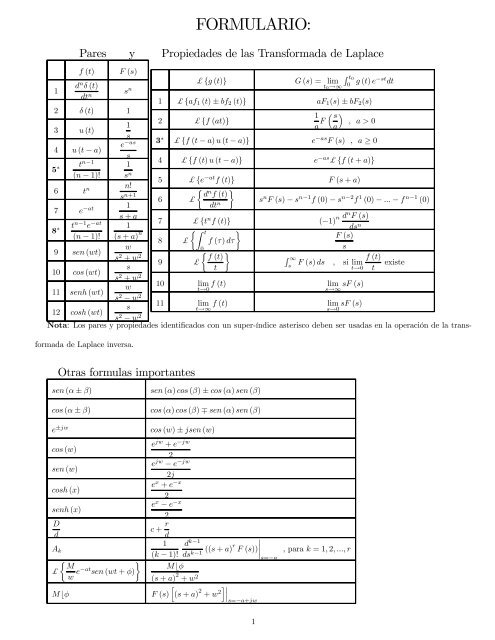
1FORMULARIO:Pares y Propiedades de las Transformada de Laplacef (t)d n δ (t)dt nF (s)2 δ (t) 13 u (t)4 u (t − a)5 ∗ t n−1(n − 1)!6 t n n!s n+17 e −at 18 ∗ t n−1 e −at(n − 1)!9 sen (wt)10 cos (wt)11 senh (wt)12 cosh (wt)£ {g (t)} G (s) = lims nt 0 →∞1³ s´2 £ {f (at)}1a F ase −ass1s n½ d n ¾f (t)6 £dt ns + a½Z t¾8 £ f (τ) dτw0½ ¾s 2 + w 2f (t)9 £sts 2 + w 2w10 lim f (t)t→0s 2 − w 2s11 lim f (t)t→∞s 2 − w 21(s + a) nR t00 g (t) e−st dt1 £ {af 1 (t) ± bf 2 (t)} aF 1 (s) ± bF 2 (s), a>03 ∗ £ {f (t − a) u (t − a)} e −as F (s) , a ≥ 04 £ {f (t) u (t − a)} e −as £ {f (t + a)}5 £ {e −at f (t)} F (s + a)s n F (s) − s n−1 f (0) − s n−2 f 1 (0) − ... − f n−1 (0)7 £ {t n f (t)} (−1) n d n F (s)ds nF (s)sR ∞f (t)F (s) ds , si lims t→0 tlim sF (s)s→∞lim sF (s)s→0Nota: Los pares y propiedades identificados con un super-índice asterisco deben ser usadas en la operación de la transformadade Laplace inversa.existeOtras formulas importantessen (α ± β)cos (α ± β)sen (α) cos (β) ± cos (α) sen (β)cos (α) cos (β) ∓ sen (α) sen (β)e ±jwcos (w) ± jsen(w)cos (w)e jw + e −jw2sen (w)e jw − e −jw2jcosh (x)e x + e −x2senh (x)e x − e −x2Dc + r dd1 d k−1A k(k − 1)! ds k−1 ((s + a)r F (s)) ¯½ ¾M Mbφ£w e−at sen (wt + φ)(s + a) 2 + w 2hMbφF (s) (s + a) 2 + wi¯¯¯s=−a+jw 21¯s=−a,parak =1, 2, ..., r

Reglas para obtener la transformada de Laplace directaAsumiendo la función f (t) =f 1 (t) f 2 (t) ...f n (t)1.- Si alguna de las funciones f k (t) es igual a u (t − a) , use la propiedad £ {f (t) u (t − a)} = e −as £ {f (t + a)} .2.- Si la función se puede descomponer en una suma, tome cada sub-función como un problema independiente y use lapropiedad #1. f (t) =f 1 (t)+f 2 (t)+... + f n (t) → F (s) =F 1 (s)+F 2 (s)+... + F n (s)3.- Usando las propiedades comenzado con la más sencilla o fácil de aplicar descomponga f (t) en funciones auxiliareshasta obtener una función que se encuentre en la tabla de pares de transformadas de Laplace.4.- Para finalizar use el par de transformada sobre la función auxiliar y substituya hacia atrás hasta obtener F (s) .4.1.- El par usado corresponderá a la sub-función f k (t) que no tenga asociada alguna propiedad.4.2- Si todas las funciones f k (t) (k =1, 2, ..., n) tienen asociadas alguna propiedad, el par usado corresponderá a la funciónf k (t) que tenga la propiedad más complicada.4.3.- Si la función para la cual existe un par no está en la forma que aparece en la tabla, haga las manipulaciones algebraicaso trigonométricas necesarias para ajustarla a la tabla.4.4.- Se debe usar sólo un par.Reglas para obtener la transformada de Laplace inversa1.- Se reconoce las propiedades de la transformada de Laplace en F (s) y se descompone F (s) en funciones auxiliares, alremover esas propiedades. (ejemplo: e −as ), hasta obtener una función racional de s.2.- Hacer mónico el denominador de G (s); es decir, el coeficiente de máximo orden es uno.3.- Calcular los ceros y polos de G (s) y cancelar los términos comunes.4.- Verificar si G (s) es estrictamente propia, es decir, el orden del polinomio del denominador es mayor que el orden delpolinomio del numerador.5.- Si G (s) no es estrictamente propia, se calcula G (s) = N (s)R (s)= C (s)+D (s) D (s) = G 1 (s)+G 2 (s), usando la técnica dedivisión de polinomios.6.- Si G (s) es estrictamente propia se expande en fracciones parciales. Si G (s) no es estrictamente propia, la expansiónsólo se hace para G 2 (s) .7.- Se obtiene la ”forma” de g (t) , usando la inversa de los pares y las propiedades de la transformada de Laplace.(g (t) =g 1 (t)+g 2 (t))8.- Se calcula el valor de los residuos para polos simples (K i ), polos múltiples (A i ) y polos conjugados (M i |φ i ).2