Capítulo 1 Métodos de residuos ponderados Funciones de prueba ...
Capítulo 1 Métodos de residuos ponderados Funciones de prueba ... Capítulo 1 Métodos de residuos ponderados Funciones de prueba ...
N 1 (ξ) = (ξ − ξ 2) (ξ 1 − ξ 2 ) = 1 (1 − ξ) 2 N 2 (ξ) = (ξ − ξ 1) (ξ 2 − ξ 1 ) = 1 2 (1 + ξ) ⎫⎪ ⎬ ⎪ ⎭ (3.26) Para k = 2 (funciones de forma cuadráticas), el elemento presenta tres nodos y las funciones de forma (ver Fig. 2.c) son N 1 (ξ) = 1 2 ξ (1 − ξ) , N 2(ξ) = ( 1 − ξ 2) , N 3 (ξ) = 1 ξ (1 + ξ) (3.27) 2 Las correspondientes funciones globales φ i se muestran en la Fig. 3. Ejemplo: sea interpolar la función g(x) = sen (x) en el intervalo 0 ≤ x ≤ 1, utilizando dos elementos cuadráticos como se muestra en la Fig. 4 Figura 4 Interpolación de g(x) usando 2 elementos cuadráticos. Los nodos están ubicados en x = 0, 0,25, 0,5, 0,75 y 1. Los valores de la función en estos puntos son 0, 0,707, 1,0, 0,707, 0, por lo que la función interpolante puede escribirse ĝ (x) = 0,707φ 2 (x) + φ 3 (x) + 0,707φ 4 (x) en donde las funciones φ i están graficadas en la Fig. 3. Se puede mostrar que el error e (x) = u (x)−û (x) entre una función exacta u y la aproximación û obtenida utilizando polinomios de Lagrange puede estimarse como ∣ h2 máx |e (x)| ≤ 0≤x≤L 8 máx ∣ ∣∣ ∣u (x) 0≤x≤L ,xx (3.28) Para elementos que emplean polinomios completos de mayor orden, el error asume la forma en la que C es independiente de h. 48 ‖e‖ ∞ = máx 0≤x≤L |e (x)| ≤ Chk+1 (3.29)
Es importante la completitud de los polinomios usados para interpolar: si, por ejemplo, las funciones de forma contienen términos proporcionales a x 0 (constantes), x 2 , x 3 , ..., x k , pero ninguno proporcional a x 1 , entonces el error será proporcional a h y no a h k+1 como indica la expresión (3.29). Si las constantes no están presentes en las funciones de interpolación, la aproximación puede no converger en absoluto. Observación: para deducir (3.29) es necesario que u presente derivadas continuas de orden ≤ k. Si la función u sólo posee derivadas de orden s con 0 < s ≤ k, entonces no importa cuanto aumentemos el grado de k en la aproximación û ya que sólo sus primeros s términos serán efectivos al aproximar u. Entonces, en lugar de (3.29) tendremos ‖e‖ ∞ = máx 0≤x≤L |e (x)| ≤ Chs (3.30) y en consecuencia no podremos mejorar la convergencia aumentando el orden del polinomio pero si disminuyendo el tamaño h del elemento. Ejercicio N ◦ 28: si un conjunto de funciones de forma es completo hasta el orden k, entonces puede interpolarse exactamente cualquier polinomio de igual o menor grado que k. a) Mostrar porque (para k ≥ 1) todo conjunto completo de funciones de forma debe satisfacer ∑k+1 N i (ξ) = 1 i=1 y ∑k+1 i=1 dN i (ξ) dξ = 0 b) Para las siguientes funciones determinar el grado del polinomio completo contenido en el conjunto. Cada conjunto de funciones de forma tiene la propiedad que N i ( ξj ) = 1 si i = j y N i ( ξj ) = 0 si i ≠ j. 1. 2. N 1 (ξ) = 1 4 (1 − ξ)2 ; N 2 (ξ) = 1 (1 + ξ)2 4 ξ 1 = −1, ξ 2 = 1 N 1 (ξ) = − 1 2 (1 − ξ) ξ ; N 2 (ξ) = ( 1 − ξ 2) 2 ; N3 (ξ) = 1 (1 + ξ) ξ 2 ξ 1 = −1, ξ 2 = 0, ξ 3 = 1 Ejercicio N ◦ 29: utilizar una malla de 3 elementos y construir interpolaciones para las funciones f (x) = x + x 2 y g (x) = cos πx para 0 < x < 1 usando (a) funciones lineales, (b) funciones de Lagrange cuadráticas. Ejercicio N ◦ 30: Derive las ecuaciones explícitas para las funciones de interpolación de Lagrange cúbicas y grafíquelas para un elemento típico. Ilustre la forma de las funciones de base φ i generadas por tales funciones para una malla consistente de tres elementos. Ejercicio N ◦ 31: Es posible representar una función g (x) sobre un elemento interpolando los valores que toma la función y sus derivadas en los extremos. a) muestre que, a tal fin, resultan funciones de forma cúbicas. b) Grafique estas funciones para un elemento típico. Las funciones de aproximación que resultan de esta forma se llaman polinomios de Hermite. 3.5. Aproximación por elementos finitos El dominio Ω se particiona en un número finito de elementos Ω e de longitud h ( ∑ h e = L). Por definición, el problema presenta cuatro subdominios en los que la solución es suave. Pero en la unión de estos subdominios pueden ocurrir discontinuidades (p.ej. x = x 2 ) a las que las funciones de interpolación no podrán acomodarse. Por tal motivo, la malla siempre se construirá de tal 49
- Page 1 and 2: Capítulo 1 Métodos de residuos po
- Page 3 and 4: ( ∂ k ∂u ) + ∂ ( k ∂u ) + F
- Page 5 and 6: δ (x − x l ) = 0 para x ≠ x l
- Page 7 and 8: p = F (1.29) en la que k y F no dep
- Page 9 and 10: La solución de los sistemas conduc
- Page 11 and 12: Una viga de longitud 1 está simple
- Page 13 and 14: Notar que K es no simétrica aun cu
- Page 15 and 16: integrando por partes el primer té
- Page 17 and 18: La sustitución de la aproximación
- Page 19 and 20: Figura 2 Ejercicio 21. a) Problema
- Page 21 and 22: Capítulo 2 El método de elementos
- Page 23 and 24: Figura 1 Aproximación de una funci
- Page 25 and 26: Figura 2 Comportamiento de tres fun
- Page 27 and 28: 2.4.1. Propiedades de la matriz K y
- Page 29 and 30: Figura 5 Descripción local y globa
- Page 31 and 32: 2.4.3.2. Cálculo del vector de car
- Page 33 and 34: de funciones. Una medida universalm
- Page 35: Figura 6 Curvas del error utilizand
- Page 38 and 39: eferiremos como ” ley de conserva
- Page 40 and 41: ambos miembros haciendo tender el p
- Page 42 and 43: 1. Condiciones de borde esenciales,
- Page 44 and 45: 2. Las condiciones de borde no pued
- Page 46 and 47: de tal modo que todo punto x en el
- Page 50 and 51: modo de ubicar un nodo en todo punt
- Page 52 and 53: Figura 5 Malla de N nudos y N-1 ele
- Page 54 and 55: 3. Condiciones naturales de Neumann
- Page 56 and 57: (c) Considere las condiciones (ii)
- Page 58 and 59: los polinomios de interpolación in
- Page 60 and 61: La derivada segunda de u respecto a
- Page 62 and 63: 4.3.3. Formulación a partir del Pr
- Page 64 and 65: ¯K = ∫ L 0 BT D B d¯x 1 = ¯K =
- Page 66 and 67: Las cargas normales al eje de la vi
- Page 68 and 69: 2. θ 1 (ξ) = ∑ 2 I=1 N I (ξ)
- Page 70 and 71: 4.5.7. Cambio de base La expresión
- Page 72 and 73: Figura 5 Viga con deformación de c
- Page 74 and 75: 4.6.1. Matriz de rigidez de una vig
- Page 76 and 77: Donde las funciones de forma son: N
- Page 78 and 79: (una para cada W J ) en función de
- Page 80 and 81: Ejercicio 1-Sea el problema de conv
- Page 82 and 83: o directamente las coordenadas noda
- Page 84 and 85: donde r es el residuo que se quiere
- Page 86: ⎡ K 3−4 = ⎢ ⎣ K 4−5 = ⎡
- Page 89 and 90: Figura 1 Conducción del calor en 2
- Page 91 and 92: 5.3. Forma variacional del problema
- Page 93 and 94: 5.5. Flujo en un medio poroso El fl
- Page 95 and 96: ortotropía coinciden con las direc
- Page 97 and 98: 5.6.5. Forma débil de la ecuación
N 1 (ξ) = (ξ − ξ 2)<br />
(ξ 1 − ξ 2 ) = 1 (1 − ξ)<br />
2<br />
N 2 (ξ) = (ξ − ξ 1)<br />
(ξ 2 − ξ 1 ) = 1 2 (1 + ξ) ⎫⎪ ⎬<br />
⎪ ⎭<br />
(3.26)<br />
Para k = 2 (funciones <strong>de</strong> forma cuadráticas), el elemento presenta tres nodos y las funciones <strong>de</strong><br />
forma (ver Fig. 2.c) son<br />
N 1 (ξ) = 1 2 ξ (1 − ξ) , N 2(ξ) = ( 1 − ξ 2) , N 3 (ξ) = 1 ξ (1 + ξ) (3.27)<br />
2<br />
Las correspondientes funciones globales φ i se muestran en la Fig. 3.<br />
Ejemplo: sea interpolar la función g(x) = sen (x) en el intervalo 0 ≤ x ≤ 1, utilizando dos<br />
elementos cuadráticos como se muestra en la Fig. 4<br />
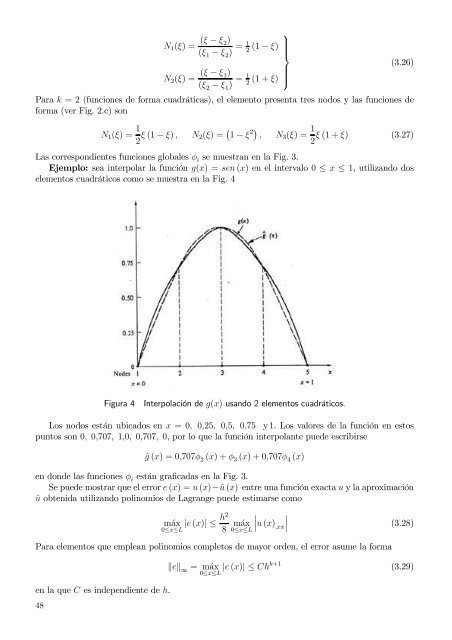
Figura 4<br />
Interpolación <strong>de</strong> g(x) usando 2 elementos cuadráticos.<br />
Los nodos están ubicados en x = 0, 0,25, 0,5, 0,75 y 1. Los valores <strong>de</strong> la función en estos<br />
puntos son 0, 0,707, 1,0, 0,707, 0, por lo que la función interpolante pue<strong>de</strong> escribirse<br />
ĝ (x) = 0,707φ 2 (x) + φ 3 (x) + 0,707φ 4 (x)<br />
en don<strong>de</strong> las funciones φ i están graficadas en la Fig. 3.<br />
Se pue<strong>de</strong> mostrar que el error e (x) = u (x)−û (x) entre una función exacta u y la aproximación<br />
û obtenida utilizando polinomios <strong>de</strong> Lagrange pue<strong>de</strong> estimarse como<br />
∣<br />
h2<br />
máx |e (x)| ≤<br />
0≤x≤L 8 máx ∣ ∣∣<br />
∣u (x)<br />
0≤x≤L ,xx (3.28)<br />
Para elementos que emplean polinomios completos <strong>de</strong> mayor or<strong>de</strong>n, el error asume la forma<br />
en la que C es in<strong>de</strong>pendiente <strong>de</strong> h.<br />
48<br />
‖e‖ ∞<br />
= máx<br />
0≤x≤L |e (x)| ≤ Chk+1 (3.29)