Control de IG. Noviembre de 2009. Tiempo del examen: 90 ... - DAC
Control de IG. Noviembre de 2009. Tiempo del examen: 90 ... - DAC
Control de IG. Noviembre de 2009. Tiempo del examen: 90 ... - DAC
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
<strong>Control</strong> <strong>de</strong> <strong>IG</strong>. <strong>Noviembre</strong> <strong>de</strong> <strong>2009.</strong> <strong>Tiempo</strong> <strong>de</strong>l <strong>examen</strong>: <strong>90</strong> minutos<br />
Pregunta 1 (3 puntos)<br />
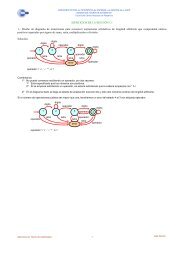
Se pi<strong>de</strong>n calcular las ecuaciones <strong>de</strong> la interpolación <strong>de</strong> Hermite que<br />
cumple las siguientes condiciones:<br />
– La curva pasa por P0(0,0) con pendiente m0=1<br />
– La curva pasa por P1(1,0)<br />
– La curva pasa por P2(2,1) con pendiente m2=0<br />
Determinar la pendiente en el punto intermedio por el algoritmo <strong>de</strong><br />
Catmull-Rom. Esbozar un gráfico <strong>de</strong>l resultado obtenido y comentar sus<br />
principales propieda<strong>de</strong>s.<br />
Solución:<br />
Apartado a)<br />
Calculamos la pendiente en P1, m1, por el algoritmo <strong>de</strong> Catmull-Rom:<br />
m1 = x2− x0 1−0<br />
=<br />
2 2 =0,5<br />
Sabemos que para cada tramo entre Pi y Pi+1, el polinomio interpolador se<br />
expresa <strong>de</strong> la forma:<br />
H i s=2s 3 −3s 2 1 x i s 3 −2s 2 sm i −2s 3 3s 2 x i1 s 3 −s 2 m i1<br />
siendo s la variable auxiliar: s= t−t i<br />
t i1−t i<br />
con s∈[0, 1]<br />
Calculamos el primer tramo <strong>de</strong>l polinomio interpolador:<br />
H 0 s=2s 3 −3s 2 1· 0 s 3 −2s 2 s·1−2s 3 3s 2 ·0s 3 −s 2 · 0,5<br />
H 0s=1,5 s 3 −2,5 s 2 s<br />
Como en este caso se tiene s= t−0<br />
1−0 =t la expresión final es:<br />
H 0t=1,5 t 3 −2,5 t 2 t , con t∈[0,1]<br />
Análogamente, para el segundo tramo tenemos:<br />
H 1 s=2s 3 −3s 2 1·0 s 3 −2s 2 s·0,5−2s 3 3s 2 ·1 s 3 −s 2 · 0<br />
H 1 s=−1,5 s 3 2s 2 0,5 s
Puesto que en este caso s= t−1<br />
2−1 =t−1 la expresión final es:<br />
H 1t=−1,5t−1 3 2 t−1 2 0,5t−1 , con t∈[1,2]<br />
Apartado b)<br />
Representando gráficamente el resultado:<br />
1.2<br />
1.0<br />
0.8<br />
0.6<br />
0.4<br />
0.2<br />
0.2<br />
x<br />
H 0<br />
0.5 1.0 1.5 2.0<br />
Vemos como la curva cumple las condiciones <strong>de</strong>l enunciado (interpola los<br />
puntos y las pendientes) y a<strong>de</strong>más es suave en el punto <strong>de</strong> empalme P1. Es<br />
fácil comprobar que la suavidad en P1 es C 2 , es <strong>de</strong>cir, la curva es continua y<br />
también lo son sus 2 primeras <strong>de</strong>rivadas.<br />
H 1<br />
t
Pregunta 2<br />
Se parte <strong>de</strong> 3 puntos en el espacio, A(1,1,1), B(3,0,0) y C(0,0,0).<br />
a) Describir cualitativamente la transformación <strong>de</strong> sólido rígido que<br />
coloca a B en el origen, a A en el eje Y y a C en el plano YZ. (3 puntos)<br />
b) Deducir <strong>de</strong> forma razonada la expresión matricial <strong>de</strong> la transformación<br />
resultante (4 puntos)<br />
Observaciones: Utilizar dibujos que ayu<strong>de</strong>n a aclarar los distintos pasos<br />
en el apartado a). Es conveniente efectuar las multiplicaciones entre<br />
matriz y vector en cada paso <strong>de</strong>l apartado b). No efectuar las<br />
multiplicaciones entre matrices al expresar la transformación final en el<br />
apartado b).<br />
Solución:<br />
Apartado a)<br />
La solución consta <strong>de</strong> 4 pasos:<br />
– Traslación <strong>de</strong> -3 unida<strong>de</strong>s a lo largo <strong>de</strong>l eje X para llevar B al origen<br />
– (usando vista <strong>de</strong> perfil): rotación <strong>de</strong> α grados negativos en torno al eje X<br />
para llevar el triángulo al plano XY, sin variar la posición <strong>de</strong>l punto B'<br />
– (usando vista <strong>de</strong> planta): rotación <strong>de</strong> β grados positivos en torno al eje Y<br />
para llevar todo el triángulo al plano YZ<br />
– (usando vista <strong>de</strong> perfil): rotación <strong>de</strong> γ grados negativos en torno al eje X<br />
para llevar a A al eje Y sin que B <strong>de</strong>je <strong>de</strong> estar en el origen ni C en el<br />
plano YZ<br />
Nota: la solución no es única, se dará como válido cualquier procedimiento que<br />
lleve a la solución correcta.<br />
Apartado b)<br />
Paso 1: traslación <strong>de</strong> -3 unida<strong>de</strong>s a lo largo <strong>de</strong>l eje X, para llevar el punto B al<br />
origen. La matriz <strong>de</strong> traslación es:<br />
0 0 −3<br />
<br />
0 1 0 0<br />
Tr=1<br />
0 0 1 0<br />
0 0 0 1<br />
Sin necesidad <strong>de</strong> hacer cálculos vemos que las coor<strong>de</strong>nadas <strong>de</strong> los puntos<br />
transformados son A'(-2,1,1), B'(0,0,0) y C'(-3,0,0), don<strong>de</strong> efectivamente el<br />
punto B ya está en el origen.<br />
Debemos seguir utilizando transformaciones <strong>de</strong> sólido rígido que no cambien la<br />
posición <strong>de</strong> B'.
Paso 2: vamos a llevar el triángulo completo al plano XY por medio <strong>de</strong> un giro<br />
en torno al eje X. Utilizando la vista <strong>de</strong> perfil, vemos que es necesario un giro<br />
<strong>de</strong> -45º. La matriz <strong>de</strong> giro es:<br />
0 0 0<br />
0 0 0<br />
0<br />
2 2<br />
0<br />
R x1−45=1 0 cos−45 −sen−45 0 2 2<br />
0 sen−45 cos−45 0<br />
0<br />
0 0 0 1=1 −2 2<br />
0<br />
2 2<br />
0 0 0 1<br />
Viendo que las posiciones <strong>de</strong> B' y C' no cambian, sólo es necesario efectuar las<br />
multiplicación entre matriz y vector para calcular las coor<strong>de</strong>nadas <strong>de</strong> A'':<br />
A''=Rx1(A')= −2 2 0<br />
B''=Rx1(B')= 0 0 0<br />
C''=Rx1(C')= −3 0 0<br />
Paso 3: utilizando la vista en planta, vemos que es necesario un giro <strong>de</strong> <strong>90</strong>º<br />
para llevar todo el triángulo al plano YZ. La matriz <strong>de</strong> la transformación es:<br />
Ry <strong>90</strong>= cos<strong>90</strong> 0 sin <strong>90</strong> 0<br />
0 1 0 0<br />
−sen<strong>90</strong> 0 cos<strong>90</strong> 0<br />
0 0 0 1=<br />
0<br />
0 1 0<br />
1<br />
0 1 0 0<br />
−1 0 0 0<br />
0 0 0<br />
Las coor<strong>de</strong>nadas <strong>de</strong> los transformados se calculan multiplicando matriz por<br />
vector. Notamos que B'' no se ve alterado:<br />
A'''=Ry(A'')= 0 2 2<br />
B'''=Ry(B'')= 0 0 0<br />
C'''=Ry(C'')= 0 0 3<br />
Paso 4: Utilizamos la vista <strong>de</strong> perfil una vez más para ver que otro giro en torno<br />
a X nos lleva A''' al eje Y, sin que C''' <strong>de</strong>je <strong>de</strong> estar en el plano YZ ni B''' en el<br />
origen.<br />
El giro es negativo, ya que es en el mismo sentido que las agujas <strong>de</strong>l reloj, y la<br />
magnitud la obtenemos por medio <strong>de</strong>l arco tangente:<br />
γ=−arctg 2<br />
=−54,73 º<br />
2
La matriz <strong>de</strong> rotación es:<br />
0 0 0 0 0 0<br />
1<br />
R<br />
0 cosγ −senγ 0 0 0,577 0,816 0<br />
x2−45=1<br />
0 senγ cosγ 0 0 −0,816 0,577 0<br />
0 0 0 1=1<br />
0 0 0<br />
y efectuando las multiplicaciones entre matriz y vector obtenemos las<br />
coor<strong>de</strong>nadas finales:<br />
A IV =Rx2(A''')= 0 2,448 0<br />
B IV =Rx2(B''')= 0 0 0<br />
C IV =Rx2(C''')= 0 2,448 1,731<br />
Observamos como A IV está en el eje Y (tiene coor<strong>de</strong>nadas X y Z nulas), B IV<br />
está en el origen, y C IV está en el plano YZ (tiene coor<strong>de</strong>nada X nula), tal como<br />
pedía el enunciado.<br />
Por tanto la transformación resultante es:<br />
T = R x2 · R y · R x1 ·Tr