Neutron Scattering - JUWEL - Forschungszentrum Jülich

More documents

Recommendations

Info

SPHERES 7 While the primary spectrometer (everything before the sample) is mainly in vacuum, the secondary spectrometer is not. To minimize neutron losses in the secondary spectrometer, the entire instrument housing can be flooded with argon. For the labcourse, we preferentially remove the argon so that participants can accede the housing. However, since refilling takes at least one full day, time constraints may prevent us from doing so. In this case, a video will be shown to present the interior of the spectrometer. 2.3 Measuring Spectra So far we have introduced a static arrangement with fixed energies Ei = Ef. Such an arrangement is actually used to measure the fraction of elastic versus total scattering, called the Debye- Waller factor for coherent scattering and the Lamb-Mössbauer factor for incoherent scattering. More often, however, one wants to measure full spectra S(Q, ω). Therefore, one must find a way to modify the energy transfer �ω = Ei − Ef. (3) This can be done using the Doppler effect: The monochromator is mounted on a linear drive that performs a cyclic motion. In the monochromator’s rest frame, the backscattered energy is always the value E0 =2.08 meV given by the lattice constant of Si(111). Depending on the monochromator’s velocity v, the value in the laboratory frame is Ei(v) = mn 2 (v0 + v) 2 where v0 = 631 m/s is the neutron velocity at E0 = mn/2 v 2 0. The Doppler drive of SPHERES has a linear amplitude of ±75 mm and achieves a velocity amplitude of ±4.7 m/s, resulting in an energy range −30.7 μeV < �ω
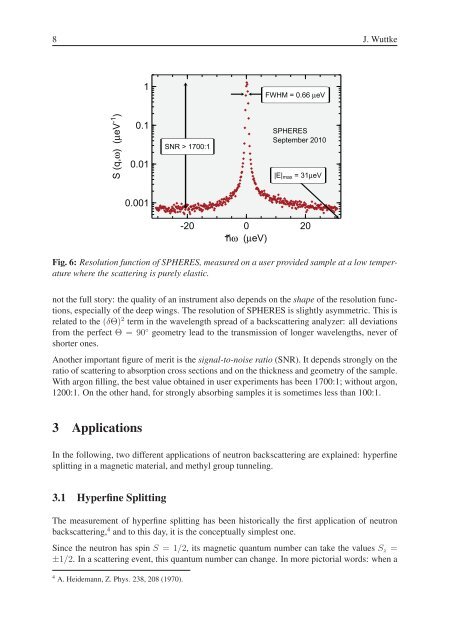
8 J. Wuttke S (q,ω) (μeV -1 ) 1 0.1 0.01 0.001 SNR > 1700:1 FWHM = 0.66 μeV SPHERES September 2010 |E|max = 31μeV -20 0 20 hω (μeV) Fig. 6: Resolution function of SPHERES, measured on a user provided sample at a low temperature where the scattering is purely elastic. not the full story: the quality of an instrument also depends on the shape of the resolution functions, especially of the deep wings. The resolution of SPHERES is slightly asymmetric. This is related to the (δΘ) 2 term in the wavelength spread of a backscattering analyzer: all deviations from the perfect Θ=90 ◦ geometry lead to the transmission of longer wavelengths, never of shorter ones. Another important figure of merit is the signal-to-noise ratio (SNR). It depends strongly on the ratio of scattering to absorption cross sections and on the thickness and geometry of the sample. With argon filling, the best value obtained in user experiments has been 1700:1; without argon, 1200:1. On the other hand, for strongly absorbing samples it is sometimes less than 100:1. 3 Applications In the following, two different applications of neutron backscattering are explained: hyperfine splitting in a magnetic material, and methyl group tunneling. 3.1 Hyperfine Splitting The measurement of hyperfine splitting has been historically the first application of neutron backscattering, 4 and to this day, it is the conceptually simplest one. Since the neutron has spin S =1/2, its magnetic quantum number can take the values Sz = ±1/2. In a scattering event, this quantum number can change. In more pictorial words: when a 4 A. Heidemann, Z. Phys. 238, 208 (1970).
Page 1 and 2:
Member of the Helmholtz Association
Page 4 and 5:
Forschungszentrum Jülich GmbH Jül
Page 6:
�� 1 PUMA
Page 9 and 10:
2 O. Sobolev, A. Teichert, N. Jünk
Page 11 and 12:
Page 13 and 14:
Page 15 and 16:
Page 17 and 18:
10 O. Sobolev, A. Teichert, N. Jün
Page 19 and 20:
Page 21 and 22:
Page 23 and 24:
2 POWDER DIFFRACTOMETER SPODI Conte
Page 25 and 26:
4 POWDER DIFFRACTOMETER SPODI 2. Ba
Page 27 and 28:
6 POWDER DIFFRACTOMETER SPODI Ewald
Page 29 and 30:
8 POWDER DIFFRACTOMETER SPODI Powde
Page 31 and 32:
10 POWDER DIFFRACTOMETER SPODI Rela
Page 33 and 34: 12 POWDER DIFFRACTOMETER SPODI Prof
Page 35 and 36: 14 POWDER DIFFRACTOMETER SPODI neut
Page 37 and 38: 16 POWDER DIFFRACTOMETER SPODI The
Page 39 and 40: 18 POWDER DIFFRACTOMETER SPODI 4 U
Page 41 and 42: 20 POWDER DIFFRACTOMETER SPODI 7. E
Page 43 and 44: 22 POWDER DIFFRACTOMETER SPODI Figu
Page 45 and 46: 24 POWDER DIFFRACTOMETER SPODI Cont
Page 47 and 48: 2 M. Meven Contents 1 Introduction
Page 49 and 50: 4 M. Meven a (hkl) Plane. Each plan
Page 51 and 52: 6 M. Meven wavelengths � in the s
Page 53 and 54: 8 M. Meven intensities (I~Z 2 ) tha
Page 55 and 56: 10 M. Meven This has to be taken in
Page 57 and 58: 12 M. Meven 4 Sample Section 4.1 In
Page 59 and 60: 14 M. Meven Fig. 8 (a) orthorhombic
Page 61 and 62: 16 M. Meven 4.3 Oxygen Position The
Page 63 and 64: 18 M. Meven To direct the secondary
Page 65 and 66: 20 M. Meven For a given spectrum
Page 67 and 68: 22 M. Meven References [1] Th. Hahn
Page 69 and 70: 24 M. Meven
Page 78 and 79: SPHERES Backscattering spectrometer
Page 80 and 81: SPHERES 3 1 Introduction Neutron ba
Page 82 and 83: SPHERES 5 Fig. 2: The monochromator
Page 86 and 87: SPHERES 9 neutron is scattered, it
Page 88 and 89: SPHERES 11 The stationary equilibri
Page 90 and 91: SPHERES 13 4. Summarize the tempera
Page 92 and 93: ________________________ DNS Neutro
Page 94 and 95: DNS 3 1 Introduction Polarized neut
Page 96 and 97: DNS 5 Monochromator horizontal- and
Page 98 and 99: DNS 7 3 Preparatory Exercises The p
Page 100 and 101: DNS 9 important and always necessar
Page 102: DNS 11 Contact �� Phone:
Page 105 and 106: 2 O. Holderer, M. Zamponi and M. Mo
Page 113 and 114: 10 O. Holderer, M. Zamponi and M. M
Page 119 and 120: 2 H. Frielinghaus, M.-S. Appavou Co
Page 121 and 122: 4 H. Frielinghaus, M.-S. Appavou Th
Page 123 and 124: 6 H. Frielinghaus, M.-S. Appavou Fi
Page 125 and 126: 8 H. Frielinghaus, M.-S. Appavou mo
Page 128 and 129: ________________________ KWS-3 Very
Page 130 and 131: KWS-3 3 1 Introduction Ultra small
Page 132 and 133: KWS-3 5 2. The standard Q-range of
Page 134 and 135:
KWS-3 7 Table 2. Samples for practi
Page 136 and 137:
KWS-3 9 References [1] Eskilden, M.
Page 138 and 139:
________________________ RESEDA Res
Page 140 and 141:
RESEDA 3 1 Introduction Neutrons ar
Page 142 and 143:
RESEDA 5 various length values l ac
Page 144 and 145:
RESEDA 7 In this expression, a norm
Page 146 and 147:
RESEDA 9 spin flip from up to down
Page 148 and 149:
RESEDA 11 The neutrons are counted
Page 150:
RESEDA 13 Contact ��
Page 153 and 154:
2 S. Mattauch and U. Rücker Conten
Page 155 and 156:
4 S. Mattauch and U. Rücker Fig. 2
Page 157 and 158:
6 S. Mattauch and U. Rücker 4 Expe
Page 159 and 160:
8 S. Mattauch and U. Rücker Contac
Page 161 and 162:
2 H. Morhenn, S. Busch, G. Simeoni
Page 163 and 164:
Page 165 and 166:
Page 167 and 168:
Page 169 and 170:
Page 171 and 172:
Page 173 and 174:
Page 175 and 176:
Page 178 and 179:
Schriften des Forschungszentrums J
Page 180 and 181:
Page 182 and 183:
show all

Neutron Scattering - JUWEL - Forschungszentrum Jülich

Create successful ePaper yourself

Delete template?

Save as template?