COMPUTATIONAL PROBLEMS IN ABSTRACT ALGEBRA.

158
44 g
h(x)
1
x 1
QO
1
el 64
e2 14
e3 14
e4 35
e5 35
e6 35
e7 65
e6 65
e9 65
el0
91
Marshall Hall Jr.
13 13 13 7 7 7
2240 2240 2240 4160 4160 4160
a a3 as c c2 c3
1 1 1 1 1 1
-1 -1 -1 1 1 1
1 1 1 0 0 0
1 1 1 0 0 0
-u1 -242 -u3 0 0 0
-u2 -ua -u1 0 0 0
-u3 -Ul -u2 0 0 0
0 0 0 Vl v2 va
0 0 0 v2 v3 Vl
0 0 0 v3 Vl v2
0 0 0 0 0 0
(5.22)
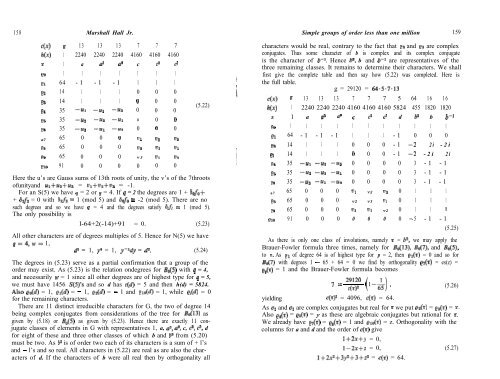
Here the u’s are Gauss sums of 13th roots of unity, the v’s of the 7throots
ofunityand U~+U~+UQ = vl+v2+~3 = -1.
For an S(5) we have q = 2 or q = 4. If q = 2 the degrees are 1 + S&+
+ Sd2 = 0 with S2fi s 1 (mod 5) and Sofa E -2 (mod 5). There are no
such degrees and so we have q = 4 and the degrees satisfy SiJ;, E 1 (mod 5).
The only possibility is
l-64+2(-14)+91 = 0. (5.23)
All other characters are of degrees multiples of 5. Hence for N(5) we have
q=4,w= 1,
d5 = 1, y4 = 1, y-ldy = d2. (5.24)
The degrees in (5.23) serve as a partial confirmation that a group of the
order may exist. As (5.23) is the relation ondegrees for Bo(5) with q = 4,
and necessarily w = 1 since all other degrees are of highest type for q = 5,
we must have 1456 S(5)‘s and so d has c(d) = 5 and then h(d) = 5824.
Also co(d) = 1, cl(d) = - 1, ez(d) = - 1 and elo(a) = 1, while pi(d) = 0
for the remaining characters.
There are 11 distinct irreducible characters for G, the two of degree 14
being complex conjugates from considerations of the tree for Bo(13) as
given by (5.18) or B,(5) as given by (5.23). Hence there are exactly 11 conjugate
classes of elements in G with representatives 1, a, as, a9, c, c2, c3, d
for eight of these and three other classes of which b and b2 from (5.20)
must be two. As b2 is of order two each of its characters is a sum of + l’s
and - l’s and so real. All characters in (5.22) are real as are also the characters
of d. If the characters of b were all real then by orthogonality all
i
Simple groups of order less than one million 159
characters would be real, contrary to the fact that e2 and es are complex
conjugates. Thus some character of b is complex and its complex conjugate
is the character of b-l. Hence b2, b and b-l are representatives of the
three remaining classes. It remains to determine their characters. We shall
first give the complete table and then say how (5.22) was completed. Here is
the full table.
h(x)
X
e0
01
e2
@3
e4
05
e6
e7
es
e9
010
g = 29120 = 64.5.7.13
g 13 13 13 7 7 7 5 64 16 16
1 2240 2240 2240 4160 4160 4160 5824 455 1820 1820
1 a a3 as
1 1 1 1
64 -1 -1 -1
14 1 1 1
14 1 1 1
35 -241 -us -u3
35 -us -243 -241
35 -u3 -241 -u2
65 0 0 0
65 0 0 0
65 0 0 0
91 0 0 0
C
1
1
0
0
0
0
0
Vl
v2
v3
0
C2
1
1
0
0
0
0
0
v2
v3
Vl
0
ti
1
1
0
0
0
0
0
v3
Vl
v2
0
d
1
-1
-1
-1
0
0
0
0
0
0
0
b2 b b-1
1 1 1
0 0 0
.2 2i -2i
.2 -2i 2i
3 -1 -1
3 -1 -1
3 -1 -1
1 1 1
1 1 1
1 1 1
-5 -1 -1
(5.25)
As there is only one class of involutions, namely z = b2, we may apply the
Brauer-Fowler formula three times, namely for Bo(13), &(7), and &(5),
to z. As el of degree 64 is of highest type for p = 2, then PI(z) = 0 and so for
Bo(7) with degrees 1 - 65 + 64 = 0 we find by orthogonality e7(z) = es(z) =
es(z) = 1 and the Brauer-Fowler formula becomes
7 = 29120
44”
1
1-s ,
( 1
(5.26)
yielding c(z)” = 4096, c(z) = 64.
As u2 and c3 are complex conjugates but real for z we put e2(t) = e3(z) = x.
Also &z) = es(z) = y as these are algebraic conjugates but rational for z.
We already have e7(t) = es(z) = 1 and elo(z) = z. Orthogonality with the
columns for a and d and the order of c(z) give
1+2x+y = 0,
l-2x+z = 0,
1+2~~+3y~+3+ze = c(z) = 64.
(5.27)