COMPUTATIONAL PROBLEMS IN ABSTRACT ALGEBRA.

378 Harvey Cohn
It is significant that the norm /N(y)1 = 1 except for those transformations
congruent to Sr (the identity), where /N(y)1 = 2.
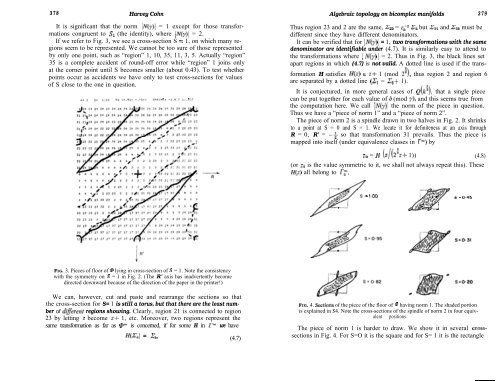
If we refer to Fig. 3, we see a cross-section S = 1, on which many regions
seem to be represented. We cannot be too sure of those represented
by only one point, such as “region” 1, 10, 35, 11, 3, 5. Actually “region”
35 is a complete accident of round-off error while “region” 1 joins only
at the corner point until S becomes smaller (about 0.43). To test whether
points occur as accidents we have only to test cross-sections for values
of S close to the one in question.
FIG. 3. Pieces of floor of @ lying in cross-section of S = 1. Note the consistency
with the symmetry on S = 1 in Fig. 2. (The R’ axis has inadvertently become
directed downward because of the direction of the paper in the printer!)
We can, however, cut and paste and rearrange the sections so that
the cross-section for S= 1 is still a torus, but that there are the least number
of d@erent regions showing. Clearly, region 21 is connected to region
23 by letting z become z+ 1, etc. Moreover, two regions represent the
same transformation as far as @- is concerned, if for some H in I‘- we have
H(Z) = &. (4.7)
Algebraic topology on bicomplex manifolds 379
Thus region 23 and 2 are the same, &a = F;~ Z2 but Zz2 and Z:zs must be
different since they have different denominators.
It can be verified that for IN(y) 1 = 1, two transformations with the same
denominator are identifiable under (4.7). It is similarly easy to attend to
the transformations where j N(y) ] = 2. Thus in Fig. 3, the black lines set
apart regions in which (4.7) is not valid. A dotted line is used if the trans-
formation H satisfies H(z) E z+ 1 (mod 29, thus region 2 and region 6
are separated by a dotted line (2s = ZS+ 1).
It is conjectured, in more general cases of f&c”), that a single piece
can be put together for each value of 6 (mod yj, and this seems true from
the computation here. We call IN(y)] the norm of the piece in question.
Thus we have a “piece of norm 1” and a “piece of norm 2”.
The piece of norm 2 is a spindle drawn in two halves in Fig. 2. It shrinks
to a point at S = 0 and S = 1. We locate it for definiteness at an axis through
R = 0, R’ = -+ so that transformation 31 prevails. Thus the piece is
mapped into itself (under equivalence classes in P) by
z. = H (z/(2+z+ 1)) (4.8)
(or z. is the value symmetric to it, we shall not always repeat this). These
H(z) all belong to I-;,-.
j . . _
/..::‘,
. . . . . .
.