- Page 1 and 2: College Trigonometry Version ⌊π
- Page 3 and 4: Table of Contents vii 10 Foundation
- Page 5 and 6: Preface Thank you for your interest
- Page 7 and 8: xi text and we have gone to great l
- Page 9 and 10: Chapter 10 Foundations of Trigonome
- Page 11 and 12: 10.1 Angles and their Measure 695 k
- Page 13 and 14: 10.1 Angles and their Measure 697 2
- Page 15 and 16: 10.1 Angles and their Measure 699 4
- Page 17 and 18: 10.1 Angles and their Measure 701 T
- Page 19 and 20: 10.1 Angles and their Measure 703 y
- Page 21 and 22: 10.1 Angles and their Measure 705 y
- Page 23 and 24: 10.1 Angles and their Measure 707 h
- Page 25 and 26: 10.1 Angles and their Measure 709 1
- Page 27 and 28: 10.1 Angles and their Measure 711 I
- Page 29 and 30: 10.1 Angles and their Measure 713 1
- Page 31 and 32: 10.1 Angles and their Measure 715 2
- Page 33 and 34: 10.2 The Unit Circle: Cosine and Si
- Page 35 and 36: 10.2 The Unit Circle: Cosine and Si
- Page 37 and 38: 10.2 The Unit Circle: Cosine and Si
- Page 39 and 40: 10.2 The Unit Circle: Cosine and Si
- Page 41 and 42: 10.2 The Unit Circle: Cosine and Si
- Page 43 and 44: 10.2 The Unit Circle: Cosine and Si
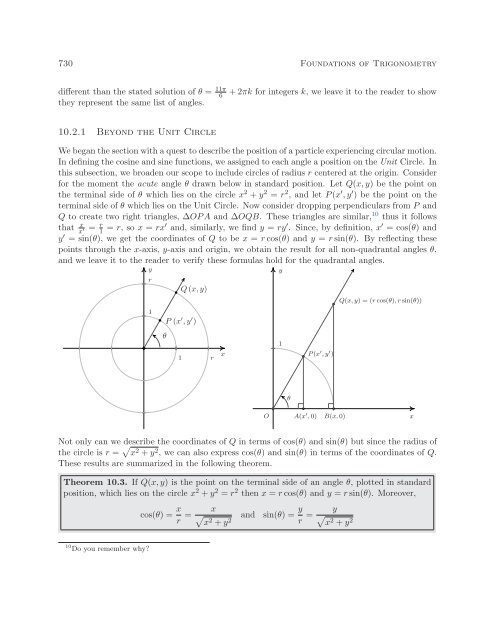
- Page 45: 10.2 The Unit Circle: Cosine and Si
- Page 49 and 50: 10.2 The Unit Circle: Cosine and Si
- Page 51 and 52: 10.2 The Unit Circle: Cosine and Si
- Page 53 and 54: 30 ◦ 1 10.2 The Unit Circle: Cosi
- Page 55 and 56: 10.2 The Unit Circle: Cosine and Si
- Page 57 and 58: 10.2 The Unit Circle: Cosine and Si
- Page 59 and 60: 10.2 The Unit Circle: Cosine and Si
- Page 61 and 62: 10.3 The Six Circular Functions and
- Page 63 and 64: 10.3 The Six Circular Functions and
- Page 65 and 66: 10.3 The Six Circular Functions and
- Page 67 and 68: 10.3 The Six Circular Functions and
- Page 69 and 70: 10.3 The Six Circular Functions and
- Page 71 and 72: 10.3 The Six Circular Functions and
- Page 73 and 74: 10.3 The Six Circular Functions and
- Page 75 and 76: 10.3 The Six Circular Functions and
- Page 77 and 78: 10.3 The Six Circular Functions and
- Page 79 and 80: 10.3 The Six Circular Functions and
- Page 81 and 82: 10.3 The Six Circular Functions and
- Page 83 and 84: 10.3 The Six Circular Functions and
- Page 85 and 86: 10.3 The Six Circular Functions and
- Page 87 and 88: 10.4 Trigonometric Identities 771 f
- Page 89 and 90: 10.4 Trigonometric Identities 773 2
- Page 91 and 92: 10.4 Trigonometric Identities 775 3
- Page 93 and 94: 10.4 Trigonometric Identities 777 2
- Page 95 and 96: 10.4 Trigonometric Identities 779 T
- Page 97 and 98:
10.4 Trigonometric Identities 781 R
- Page 99 and 100:
10.4 Trigonometric Identities 783 2
- Page 101 and 102:
10.4 Trigonometric Identities 785 I
- Page 103 and 104:
10.4 Trigonometric Identities 787 1
- Page 105 and 106:
10.4 Trigonometric Identities 789 5
- Page 107 and 108:
10.5 Graphs of the Trigonometric Fu
- Page 109 and 110:
10.5 Graphs of the Trigonometric Fu
- Page 111 and 112:
10.5 Graphs of the Trigonometric Fu
- Page 113 and 114:
10.5 Graphs of the Trigonometric Fu
- Page 115 and 116:
10.5 Graphs of the Trigonometric Fu
- Page 117 and 118:
10.5 Graphs of the Trigonometric Fu
- Page 119 and 120:
10.5 Graphs of the Trigonometric Fu
- Page 121 and 122:
10.5 Graphs of the Trigonometric Fu
- Page 123 and 124:
10.5 Graphs of the Trigonometric Fu
- Page 125 and 126:
10.5 Graphs of the Trigonometric Fu
- Page 127 and 128:
10.5 Graphs of the Trigonometric Fu
- Page 129 and 130:
10.5 Graphs of the Trigonometric Fu
- Page 131 and 132:
10.5 Graphs of the Trigonometric Fu
- Page 133 and 134:
10.5 Graphs of the Trigonometric Fu
- Page 135 and 136:
10.6 The Inverse Trigonometric Func
- Page 137 and 138:
10.6 The Inverse Trigonometric Func
- Page 139 and 140:
10.6 The Inverse Trigonometric Func
- Page 141 and 142:
10.6 The Inverse Trigonometric Func
- Page 143 and 144:
10.6 The Inverse Trigonometric Func
- Page 145 and 146:
10.6 The Inverse Trigonometric Func
- Page 147 and 148:
10.6 The Inverse Trigonometric Func
- Page 149 and 150:
10.6 The Inverse Trigonometric Func
- Page 151 and 152:
10.6 The Inverse Trigonometric Func
- Page 153 and 154:
10.6 The Inverse Trigonometric Func
- Page 155 and 156:
10.6 The Inverse Trigonometric Func
- Page 157 and 158:
10.6 The Inverse Trigonometric Func
- Page 159 and 160:
10.6 The Inverse Trigonometric Func
- Page 161 and 162:
10.6 The Inverse Trigonometric Func
- Page 163 and 164:
10.6 The Inverse Trigonometric Func
- Page 165 and 166:
10.6 The Inverse Trigonometric Func
- Page 167 and 168:
10.6 The Inverse Trigonometric Func
- Page 169 and 170:
10.6 The Inverse Trigonometric Func
- Page 171 and 172:
10.6 The Inverse Trigonometric Func
- Page 173 and 174:
10.7 Trigonometric Equations and In
- Page 175 and 176:
10.7 Trigonometric Equations and In
- Page 177 and 178:
10.7 Trigonometric Equations and In
- Page 179 and 180:
10.7 Trigonometric Equations and In
- Page 181 and 182:
10.7 Trigonometric Equations and In
- Page 183 and 184:
10.7 Trigonometric Equations and In
- Page 185 and 186:
10.7 Trigonometric Equations and In
- Page 187 and 188:
10.7 Trigonometric Equations and In
- Page 189 and 190:
10.7 Trigonometric Equations and In
- Page 191 and 192:
10.7 Trigonometric Equations and In
- Page 193 and 194:
10.7 Trigonometric Equations and In
- Page 195 and 196:
10.7 Trigonometric Equations and In
- Page 197 and 198:
Chapter 11 Applications of Trigonom
- Page 199 and 200:
11.1 Applications of Sinusoids 883
- Page 201 and 202:
11.1 Applications of Sinusoids 885
- Page 203 and 204:
11.1 Applications of Sinusoids 887
- Page 205 and 206:
11.1 Applications of Sinusoids 889
- Page 207 and 208:
11.1 Applications of Sinusoids 891
- Page 209 and 210:
11.1 Applications of Sinusoids 893
- Page 211 and 212:
11.1 Applications of Sinusoids 895
- Page 213 and 214:
11.2 The Law of Sines 897 minimizes
- Page 215 and 216:
11.2 The Law of Sines 899 a angle-s
- Page 217 and 218:
11.2 The Law of Sines 901 determine
- Page 219 and 220:
11.2 The Law of Sines 903 Let x den
- Page 221 and 222:
11.2 The Law of Sines 905 24. Along
- Page 223 and 224:
11.2 The Law of Sines 907 33. The a
- Page 225 and 226:
11.2 The Law of Sines 909 25. (a)
- Page 227 and 228:
11.3 The Law of Cosines 911 of B ar
- Page 229 and 230:
11.3 The Law of Cosines 913 the pre
- Page 231 and 232:
11.3 The Law of Cosines 915 A 2 = =
- Page 233 and 234:
11.3 The Law of Cosines 917 22. A n
- Page 235 and 236:
11.4 Polar Coordinates 919 11.4 Pol
- Page 237 and 238:
11.4 Polar Coordinates 921 The poin
- Page 239 and 240:
11.4 Polar Coordinates 923 4. We mo
- Page 241 and 242:
11.4 Polar Coordinates 925 Solution
- Page 243 and 244:
11.4 Polar Coordinates 927 Solution
- Page 245 and 246:
11.4 Polar Coordinates 929 algebrai
- Page 247 and 248:
11.4 Polar Coordinates 931 45. ( )
- Page 249 and 250:
11.4 Polar Coordinates 933 5. ( 12,
- Page 251 and 252:
11.4 Polar Coordinates 935 13. (
- Page 253 and 254:
11.4 Polar Coordinates 937 73. r =7
- Page 255 and 256:
11.5 Graphs of Polar Equations 939
- Page 257 and 258:
11.5 Graphs of Polar Equations 941
- Page 259 and 260:
11.5 Graphs of Polar Equations 943
- Page 261 and 262:
11.5 Graphs of Polar Equations 945
- Page 263 and 264:
11.5 Graphs of Polar Equations 947
- Page 265 and 266:
11.5 Graphs of Polar Equations 949
- Page 267 and 268:
11.5 Graphs of Polar Equations 951
- Page 269 and 270:
11.5 Graphs of Polar Equations 953
- Page 271 and 272:
11.5 Graphs of Polar Equations 955
- Page 273 and 274:
11.5 Graphs of Polar Equations 957
- Page 275 and 276:
11.5 Graphs of Polar Equations 959
- Page 277 and 278:
11.5 Graphs of Polar Equations 961
- Page 279 and 280:
11.5 Graphs of Polar Equations 963
- Page 281 and 282:
11.5 Graphs of Polar Equations 965
- Page 283 and 284:
11.5 Graphs of Polar Equations 967
- Page 285 and 286:
11.5 Graphs of Polar Equations 969
- Page 287 and 288:
11.5 Graphs of Polar Equations 971
- Page 289 and 290:
11.6 Hooked on Conics Again 973 11.
- Page 291 and 292:
11.6 Hooked on Conics Again 975 Exa
- Page 293 and 294:
11.6 Hooked on Conics Again 977 The
- Page 295 and 296:
11.6 Hooked on Conics Again 979 We
- Page 297 and 298:
11.6 Hooked on Conics Again 981 1.
- Page 299 and 300:
11.6 Hooked on Conics Again 983 The
- Page 301 and 302:
11.6 Hooked on Conics Again 985 In
- Page 303 and 304:
11.6 Hooked on Conics Again 987 11.
- Page 305 and 306:
11.6 Hooked on Conics Again 989 2 9
- Page 307 and 308:
11.7 Polar Form of Complex Numbers
- Page 309 and 310:
11.7 Polar Form of Complex Numbers
- Page 311 and 312:
11.7 Polar Form of Complex Numbers
- Page 313 and 314:
11.7 Polar Form of Complex Numbers
- Page 315 and 316:
11.7 Polar Form of Complex Numbers
- Page 317 and 318:
11.7 Polar Form of Complex Numbers
- Page 319 and 320:
11.7 Polar Form of Complex Numbers
- Page 321 and 322:
11.7 Polar Form of Complex Numbers
- Page 323 and 324:
11.7 Polar Form of Complex Numbers
- Page 325 and 326:
11.7 Polar Form of Complex Numbers
- Page 327 and 328:
11.7 Polar Form of Complex Numbers
- Page 329 and 330:
11.8 Vectors 1013 Q ′ (1, 7) up 4
- Page 331 and 332:
11.8 Vectors 1015 ⃗v + ⃗w = 〈
- Page 333 and 334:
11.8 Vectors 1017 ⃗v − ⃗w =
- Page 335 and 336:
11.8 Vectors 1019 The remaining pro
- Page 337 and 338:
11.8 Vectors 1021 ‖k⃗v‖ = ‖
- Page 339 and 340:
11.8 Vectors 1023 at the origin, th
- Page 341 and 342:
11.8 Vectors 1025 Geometrically, th
- Page 343 and 344:
11.8 Vectors 1027 11.8.1 Exercises
- Page 345 and 346:
11.8 Vectors 1029 44. ⃗v = 〈−
- Page 347 and 348:
11.8 Vectors 1031 11.8.2 Answers 1.
- Page 349 and 350:
11.8 Vectors 1033 47. ‖⃗v‖ =2
- Page 351 and 352:
11.9 The Dot Product and Projection
- Page 353 and 354:
11.9 The Dot Product and Projection
- Page 355 and 356:
11.9 The Dot Product and Projection
- Page 357 and 358:
11.9 The Dot Product and Projection
- Page 359 and 360:
11.9 The Dot Product and Projection
- Page 361 and 362:
11.9 The Dot Product and Projection
- Page 363 and 364:
11.9 The Dot Product and Projection
- Page 365 and 366:
11.10 Parametric Equations 1049 obj
- Page 367 and 368:
11.10 Parametric Equations 1051 2.
- Page 369 and 370:
11.10 Parametric Equations 1053 Now
- Page 371 and 372:
11.10 Parametric Equations 1055 5.
- Page 373 and 374:
11.10 Parametric Equations 1057 Our
- Page 375 and 376:
11.10 Parametric Equations 1059 11.
- Page 377 and 378:
11.10 Parametric Equations 1061 Sup
- Page 379 and 380:
11.10 Parametric Equations 1063 11.
- Page 381 and 382:
11.10 Parametric Equations 1065 13.
- Page 383 and 384:
11.10 Parametric Equations 1067 23.
- Page 385 and 386:
Index n th root of a complex number
- Page 387 and 388:
Index 1071 central angle, 701 chang
- Page 389 and 390:
Index 1073 reflective property, 523
- Page 391 and 392:
Index 1075 matrix, multiplicative,
- Page 393 and 394:
Index 1077 midpoint definition of,
- Page 395 and 396:
Index 1079 instantaneous, 161, 472
- Page 397 and 398:
Index 1081 inconsistent, 553 indepe