fluid_mechanics
506 Chapter 9 ■ Flow over Immersed Bodies for the smooth golf ball d 1 2 10.00238 slugs ft 3 21200 fts2 2 p 2 4 a1.69 12 ftb 10.512 0.378 lb (Ans) and for the table tennis ball d 1 2 10.00238 slugs ft 3 2160 fts2 2 p 2 4 a1.50 12 ftb 10.502 0.0263 lb (Ans) The corresponding decelerations are a dm gdw, where m is the mass of the ball. Thus, the deceleration relative to the acceleration of gravity, ag 1i.e., the number of g’s deceleration2 is ag dw or a 0.185 lb 1.86 for the standard golf ball g 0.0992 lb a 0.378 lb 3.81 for the smooth golf ball g 0.0992 lb a 0.0263 lb 4.77 for the table tennis ball g 0.00551 lb (Ans) (Ans) (Ans) COMMENTS Note that there is a considerably smaller deceleration for the rough golf ball than for the smooth one. Because of its much larger drag-to-mass ratio, the table tennis ball slows down relatively quickly and does not travel as far as the golf ball. Note that with U 60 fts the standard golf ball has a drag of d 0.0200 lb and a deceleration of ag 0.202, considerably less than the ag 4.77 of the table tennis ball. Conversely, a table tennis ball hit from a tee at 200 fts would decelerate at a rate of a 1740 fts 2 , or ag 54.1. It would not travel nearly as far as the golf ball. By repeating the above calculations, the drag as a function of speed for both a standard golf ball and a smooth golf ball is shown in Fig. E9.12. The Reynolds number range for which a rough golf ball has smaller drag than a smooth one (i.e., 4 10 4 to 3.6 10 5 ) corresponds to a flight velocity range of 45 U 400 ft/s. This is comfortably within the range of most golfers. (The fastest tee shot by top professional golfers is approximately 280 ft/s.) As discussed in Section 9.4.2, the dimples (roughness) on a golf ball also help produce a lift (due to the spin of the ball) that allows the ball to travel farther than a smooth ball. , lb 1.2 1 0.8 0.6 0.4 0.2 Smooth golf ball Standard golf ball 0 0 100 200 300 400 500 U, ft/s F I G U R E E9.12 F l u i d s i n t h e N e w s Dimpled baseball bats For many years it has been known that dimples on golf balls can create a turbulent boundary layer and reduce the aerodynamic drag, allowing longer drives than with smooth balls. Thus, why not put dimples on baseball bats so that tomorrow’s baseball sluggers can swing the bat faster and, therefore, hit the ball farther? MIT instructor Jeffery De Tullio pondered that question, performed experiments with dimpled bats to determine the answer, and received a patent for his dimpled bat invention. The result is that a batter can swing a dimpled bat approximately 3 to 5% faster than a smooth bat. Theoretically, this extra speed will translate to an extra 10 to 15 ft distance on a long hit. (See Problem 9.89.) V9.12 Jet ski The drag coefficient for surface ships is a function of the Froude number. Froude Number Effects. Another parameter on which the drag coefficient may be strongly dependent is the Froude number, Fr U 1g/. As is discussed in Chapter 10, the Froude number is a ratio of the free-stream speed to a typical wave speed on the interface of two fluids, such as the surface of the ocean. An object moving on the surface, such as a ship, often produces waves that require a source of energy to generate. This energy comes from the ship and is manifest as a drag. [Recall that the rate of energy production 1power2 equals speed times force.] The nature of the waves produced often depends on the Froude number of the flow and the shape of the object—the waves generated by a water skier “plowing” through the water at a low speed 1low Fr2 are different than those generated by the skier “planing” along the surface at high speed 1large Fr2. Thus, the drag coefficient for surface ships is a function of Reynolds number 1viscous effects2 and Froude number 1wave-making effects2; C D f1Re, Fr2. As was discussed in Chapter 7, it is often quite difficult to run model tests under conditions similar to those of the prototype 1i.e., same Re and Fr for surface ships2. Fortunately, the viscous and wave effects can often be separated, with the total drag being the sum of the drag of these individual effects. A detailed account of this important topic can be found in standard texts 1Ref. 112. As is indicated in Fig. 9.26, the wave-making drag, d w , can be a complex function of the Froude number and the body shape. The rather “wiggly” dependence of the wave drag coefficient,
9.3 Drag 507 0.0015 U Hull with no bow bulb 0.0010 C Dw w C D = __________ 1__ U 2 2 2 ρ Fr = U U Hull with bow bulb 0.0005 0 0.1 0.2 Design speed, Fr = 0.267 F I G U R E 9.26 Typical drag coefficient data as a function of Froude number and hull characteristics for that portion of the drag due to the generation of waves (adapted from Ref. 25). ____ √g 0.3 0.4 pole flag The drag on a complex body can be approximated as the sum of the drag on its parts. C Dw d w1rU 2 / 2 22, on the Froude number shown is typical. It results from the fact that the structure of the waves produced by the hull is a strong function of the ship speed or, in dimensionless form, the Froude number. This wave structure is also a function of the body shape. For example, the bow wave, which is often the major contributor to the wave drag, can be reduced by use of an appropriately designed bulb on the bow, as is indicated in Fig. 9.26. In this instance the streamlined body 1hull without a bulb2 has more drag than the less streamlined one. Composite Body Drag. Approximate drag calculations for a complex body can often be obtained by treating the body as a composite collection of its various parts. For example, the total force on a flag pole because of the wind (see the figure in the margin) can be approximated by adding the aerodynamic drag produced by the various components involved—the drag on the flag and the drag on the pole. In some cases considerable care must be taken in such an approach because of the interactions between the various parts. It may not be correct to merely add the drag of the components to obtain the drag of the entire object, although such approximations are often reasonable. E XAMPLE 9.13 Drag on a Composite Body GIVEN A 60-mph 1i.e., 88-fps2 wind blows past the water tower shown in Fig. E9.13a. U = 60 mph = 88 fps D s s FIND Estimate the moment 1torque2, M, needed at the base to keep the tower from tipping over. D s = 40 ft D c = 15 ft b = 50 ft b D c b + D s /2 c b/2 SOLUTION We treat the water tower as a sphere resting on a circular cylinder and assume that the total drag is the sum of the drag from these parts. The free-body diagram of the tower is shown in Fig. (a) F I G U R E E9.13 M R y (b) R x
- Page 480 and 481: 456 Chapter 8 ■ Viscous Flow in P
- Page 482 and 483: 458 Chapter 8 ■ Viscous Flow in P
- Page 484 and 485: 460 Chapter 8 ■ Viscous Flow in P
- Page 486 and 487: 462 Chapter 9 ■ Flow over Immerse
- Page 488 and 489: 464 Chapter 9 ■ Flow over Immerse
- Page 490 and 491: 466 Chapter 9 ■ Flow over Immerse
- Page 492 and 493: 468 Chapter 9 ■ Flow over Immerse
- Page 494 and 495: 470 Chapter 9 ■ Flow over Immerse
- Page 496 and 497: 472 Chapter 9 ■ Flow over Immerse
- Page 498 and 499: 474 Chapter 9 ■ Flow over Immerse
- Page 500 and 501: 476 Chapter 9 ■ Flow over Immerse
- Page 502 and 503: 478 Chapter 9 ■ Flow over Immerse
- Page 504 and 505: 480 Chapter 9 ■ Flow over Immerse
- Page 506 and 507: 482 Chapter 9 ■ Flow over Immerse
- Page 508 and 509: 484 Chapter 9 ■ Flow over Immerse
- Page 510 and 511: 486 Chapter 9 ■ Flow over Immerse
- Page 512 and 513: 488 Chapter 9 ■ Flow over Immerse
- Page 514 and 515: 490 Chapter 9 ■ Flow over Immerse
- Page 516 and 517: 492 Chapter 9 ■ Flow over Immerse
- Page 518 and 519: 494 Chapter 9 ■ Flow over Immerse
- Page 520 and 521: 496 Chapter 9 ■ Flow over Immerse
- Page 522 and 523: 498 Chapter 9 ■ Flow over Immerse
- Page 524 and 525: 500 Chapter 9 ■ Flow over Immerse
- Page 526 and 527: 502 Chapter 9 ■ Flow over Immerse
- Page 528 and 529: 504 Chapter 9 ■ Flow over Immerse
- Page 532 and 533: 508 Chapter 9 ■ Flow over Immerse
- Page 534 and 535: 510 Chapter 9 ■ Flow over Immerse
- Page 536 and 537: 512 Chapter 9 ■ Flow over Immerse
- Page 538 and 539: 514 Chapter 9 ■ Flow over Immerse
- Page 540 and 541: 516 Chapter 9 ■ Flow over Immerse
- Page 542 and 543: 518 Chapter 9 ■ Flow over Immerse
- Page 544 and 545: 520 Chapter 9 ■ Flow over Immerse
- Page 546 and 547: 522 Chapter 9 ■ Flow over Immerse
- Page 548 and 549: 524 Chapter 9 ■ Flow over Immerse
- Page 550 and 551: 526 Chapter 9 ■ Flow over Immerse
- Page 552 and 553: 528 Chapter 9 ■ Flow over Immerse
- Page 554 and 555: ∋ 530 Chapter 9 ■ Flow over Imm
- Page 556 and 557: 532 Chapter 9 ■ Flow over Immerse
- Page 558 and 559: 10 Open-Channel Flow CHAPTER OPENIN
- Page 560 and 561: 536 Chapter 10 ■ Open-Channel Flo
- Page 562 and 563: 538 Chapter 10 ■ Open-Channel Flo
- Page 564 and 565: 540 Chapter 10 ■ Open-Channel Flo
- Page 566 and 567: 542 Chapter 10 ■ Open-Channel Flo
- Page 568 and 569: 544 Chapter 10 ■ Open-Channel Flo
- Page 570 and 571: 546 Chapter 10 ■ Open-Channel Flo
- Page 572 and 573: 548 Chapter 10 ■ Open-Channel Flo
- Page 574 and 575: 550 Chapter 10 ■ Open-Channel Flo
- Page 576 and 577: 552 Chapter 10 ■ Open-Channel Flo
- Page 578 and 579: 554 Chapter 10 ■ Open-Channel Flo
506 Chapter 9 ■ Flow over Immersed Bodies<br />
for the smooth golf ball<br />
d 1 2 10.00238 slugs ft 3 21200 fts2 2 p 2<br />
4 a1.69 12 ftb 10.512<br />
0.378 lb<br />
(Ans)<br />
and for the table tennis ball<br />
d 1 2 10.00238 slugs ft 3 2160 fts2 2 p 2<br />
4 a1.50 12 ftb 10.502<br />
0.0263 lb<br />
(Ans)<br />
The corresponding decelerations are a dm gdw,<br />
where m is the mass of the ball. Thus, the deceleration relative to<br />
the acceleration of gravity, ag 1i.e., the number of g’s deceleration2<br />
is ag dw or<br />
a 0.185 lb<br />
1.86 for the standard golf ball<br />
g 0.0992 lb<br />
a 0.378 lb<br />
3.81 for the smooth golf ball<br />
g 0.0992 lb<br />
a 0.0263 lb<br />
4.77 for the table tennis ball<br />
g 0.00551 lb<br />
(Ans)<br />
(Ans)<br />
(Ans)<br />
COMMENTS Note that there is a considerably smaller deceleration<br />
for the rough golf ball than for the smooth one. Because of<br />
its much larger drag-to-mass ratio, the table tennis ball slows down<br />
relatively quickly and does not travel as far as the golf ball. Note<br />
that with U 60 fts the standard golf ball has a drag of<br />
d 0.0200 lb and a deceleration of ag 0.202, considerably<br />
less than the ag 4.77 of the table tennis ball. Conversely, a<br />
table tennis ball hit from a tee at 200 fts would decelerate at a<br />
rate of a 1740 fts 2 , or ag 54.1. It would not travel nearly<br />
as far as the golf ball.<br />
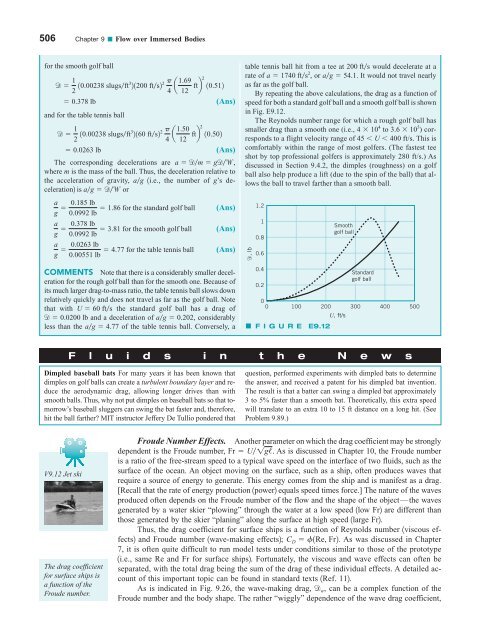
By repeating the above calculations, the drag as a function of<br />
speed for both a standard golf ball and a smooth golf ball is shown<br />
in Fig. E9.12.<br />
The Reynolds number range for which a rough golf ball has<br />
smaller drag than a smooth one (i.e., 4 10 4 to 3.6 10 5 ) corresponds<br />
to a flight velocity range of 45 U 400 ft/s. This is<br />
comfortably within the range of most golfers. (The fastest tee<br />
shot by top professional golfers is approximately 280 ft/s.) As<br />
discussed in Section 9.4.2, the dimples (roughness) on a golf<br />
ball also help produce a lift (due to the spin of the ball) that allows<br />
the ball to travel farther than a smooth ball.<br />
, lb<br />
1.2<br />
1<br />
0.8<br />
0.6<br />
0.4<br />
0.2<br />
Smooth<br />
golf ball<br />
Standard<br />
golf ball<br />
0<br />
0 100 200 300 400 500<br />
U, ft/s<br />
F I G U R E E9.12<br />
F l u i d s i n t h e N e w s<br />
Dimpled baseball bats For many years it has been known that<br />
dimples on golf balls can create a turbulent boundary layer and reduce<br />
the aerodynamic drag, allowing longer drives than with<br />
smooth balls. Thus, why not put dimples on baseball bats so that tomorrow’s<br />
baseball sluggers can swing the bat faster and, therefore,<br />
hit the ball farther? MIT instructor Jeffery De Tullio pondered that<br />
question, performed experiments with dimpled bats to determine<br />
the answer, and received a patent for his dimpled bat invention.<br />
The result is that a batter can swing a dimpled bat approximately<br />
3 to 5% faster than a smooth bat. Theoretically, this extra speed<br />
will translate to an extra 10 to 15 ft distance on a long hit. (See<br />
Problem 9.89.)<br />
V9.12 Jet ski<br />
The drag coefficient<br />
for surface ships is<br />
a function of the<br />
Froude number.<br />
Froude Number Effects. Another parameter on which the drag coefficient may be strongly<br />
dependent is the Froude number, Fr U 1g/. As is discussed in Chapter 10, the Froude number<br />
is a ratio of the free-stream speed to a typical wave speed on the interface of two <strong>fluid</strong>s, such as the<br />
surface of the ocean. An object moving on the surface, such as a ship, often produces waves that<br />
require a source of energy to generate. This energy comes from the ship and is manifest as a drag.<br />
[Recall that the rate of energy production 1power2 equals speed times force.] The nature of the waves<br />
produced often depends on the Froude number of the flow and the shape of the object—the waves<br />
generated by a water skier “plowing” through the water at a low speed 1low Fr2 are different than<br />
those generated by the skier “planing” along the surface at high speed 1large Fr2.<br />
Thus, the drag coefficient for surface ships is a function of Reynolds number 1viscous effects2<br />
and Froude number 1wave-making effects2; C D f1Re, Fr2. As was discussed in Chapter<br />
7, it is often quite difficult to run model tests under conditions similar to those of the prototype<br />
1i.e., same Re and Fr for surface ships2. Fortunately, the viscous and wave effects can often be<br />
separated, with the total drag being the sum of the drag of these individual effects. A detailed account<br />
of this important topic can be found in standard texts 1Ref. 112.<br />
As is indicated in Fig. 9.26, the wave-making drag, d w , can be a complex function of the<br />
Froude number and the body shape. The rather “wiggly” dependence of the wave drag coefficient,