fluid_mechanics

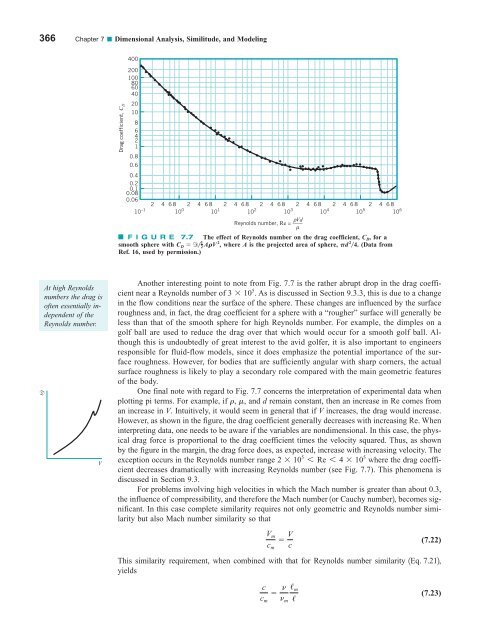
366 Chapter 7 ■ Dimensional Analysis, Similitude, and Modeling
400
Drag coefficient, C D
200
100
80
60
40
20
10
8
6
4
2
1
0.8
0.6
0.4
0.2
0.1
0.08
0.06
2 4 68 2 4 68 2 4 68 2 4 68 2 4 68 2 4 68 2 4 68
10 –1 10 0 10 1 10 2 10 3 10 4 10 5 10 6
Reynolds number, Re = ____ ρ Vd
μ
F I G U R E 7.7 The effect of Reynolds number on the drag coefficient, C D , for a
smooth sphere with C where A is the projected area of sphere, Pd 2 D d 1 2 ARV 2 ,
4. (Data from
Ref. 16, used by permission.)
At high Reynolds
numbers the drag is
often essentially independent
of the
Reynolds number.
V
Another interesting point to note from Fig. 7.7 is the rather abrupt drop in the drag coefficient
near a Reynolds number of 3 10 5 . As is discussed in Section 9.3.3, this is due to a change
in the flow conditions near the surface of the sphere. These changes are influenced by the surface
roughness and, in fact, the drag coefficient for a sphere with a “rougher” surface will generally be
less than that of the smooth sphere for high Reynolds number. For example, the dimples on a
golf ball are used to reduce the drag over that which would occur for a smooth golf ball. Although
this is undoubtedly of great interest to the avid golfer, it is also important to engineers
responsible for fluid-flow models, since it does emphasize the potential importance of the surface
roughness. However, for bodies that are sufficiently angular with sharp corners, the actual
surface roughness is likely to play a secondary role compared with the main geometric features
of the body.
One final note with regard to Fig. 7.7 concerns the interpretation of experimental data when
plotting pi terms. For example, if r,
m, and d remain constant, then an increase in Re comes from
an increase in V. Intuitively, it would seem in general that if V increases, the drag would increase.
However, as shown in the figure, the drag coefficient generally decreases with increasing Re. When
interpreting data, one needs to be aware if the variables are nondimensional. In this case, the physical
drag force is proportional to the drag coefficient times the velocity squared. Thus, as shown
by the figure in the margin, the drag force does, as expected, increase with increasing velocity. The
exception occurs in the Reynolds number range 2 10 5 6 Re 6 4 10 5 where the drag coefficient
decreases dramatically with increasing Reynolds number (see Fig. 7.7). This phenomena is
discussed in Section 9.3.
For problems involving high velocities in which the Mach number is greater than about 0.3,
the influence of compressibility, and therefore the Mach number 1or Cauchy number2, becomes significant.
In this case complete similarity requires not only geometric and Reynolds number similarity
but also Mach number similarity so that
V m
c m
V c
(7.22)
This similarity requirement, when combined with that for Reynolds number similarity 1Eq. 7.212,
yields
c
c m
n n m
/ m
/
(7.23)