You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
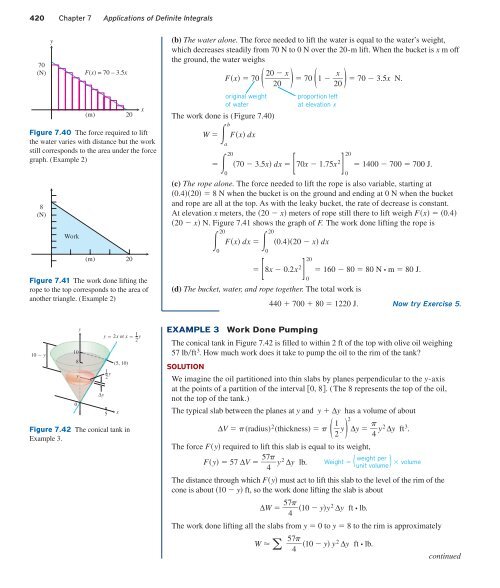
420 Chapter 7 Applications of Definite Integrals<br />
70<br />
(N)<br />
y<br />
F(x) = 70 – 3.5x<br />
(m) 20<br />
Figure 7.40 The force required to lift<br />
the water varies with distance but the work<br />
still corresponds to the area under the force<br />
graph. (Example 2)<br />
8<br />
(N)<br />
Work<br />
(m)<br />
20<br />
Figure 7.41 The work done lifting the<br />
rope to the top corresponds to the area of<br />
another triangle. (Example 2)<br />
x<br />
(b) The water alone. The force needed to lift the water is equal to the water’s weight,<br />
which decreases steadily from 70 N to 0 N over the 20-m lift. When the bucket is x m off<br />
the ground, the water weighs<br />
Fx 70 ( 20 x<br />
20<br />
) ( 70 1 x<br />
70 3.5x N.<br />
20<br />
The work done is (Figure 7.40)<br />
W b<br />
a<br />
20<br />
0<br />
Fx dx<br />
70 3.5x dx <br />
[<br />
)<br />
20<br />
70x 1.75x2]<br />
1400 700 700 J.<br />
0<br />
(c) The rope alone. The force needed to lift the rope is also variable, starting at<br />
0.420 8 N when the bucket is on the ground and ending at 0 N when the bucket<br />
and rope are all at the top. As with the leaky bucket, the rate of decrease is constant.<br />
At elevation x meters, the 20 x meters of rope still there to lift weigh Fx 0.4<br />
20 x N. Figure 7.41 shows the graph of F. The work done lifting the rope is<br />
Fx dx 20<br />
0.420 x dx<br />
20<br />
0<br />
original weight<br />
of water<br />
proportion left<br />
at elevation x<br />
0<br />
20<br />
<br />
[<br />
8x 0.2x2]<br />
160 80 80 N • m 80 J.<br />
0<br />
(d) The bucket, water, and rope together. The total work is<br />
440 700 80 1220 J. Now try Exercise 5.<br />
10 y<br />
y<br />
10<br />
8<br />
0<br />
y<br />
Δy<br />
y 2x or x<br />
1<br />
y<br />
2<br />
1<br />
y<br />
2<br />
5<br />
(5, 10)<br />
Figure 7.42 The conical tank in<br />
Example 3.<br />
x<br />
EXAMPLE 3<br />
Work Done Pumping<br />
The conical tank in Figure 7.42 is filled to within 2 ft of the top with olive oil weighing<br />
57 lbft 3 . How much work does it take to pump the oil to the rim of the tank?<br />
SOLUTION<br />
We imagine the oil partitioned into thin slabs by planes perpendicular to the y-axis<br />
at the points of a partition of the interval 0, 8. (The 8 represents the top of the oil,<br />
not the top of the tank.)<br />
The typical slab between the planes at y and y Δy has a volume of about<br />
2<br />
Δy p 4 y2 Δy ft 3 .<br />
ΔV p(radius) 2 (thickness) p ( 1 2 y )<br />
The force Fy required to lift this slab is equal to its weight,<br />
Fy 57 ΔV 57 p<br />
y<br />
4<br />
2 Δy lb.<br />
weight per<br />
Weight ( unit volume ) volume<br />
The distance through which Fy must act to lift this slab to the level of the rim of the<br />
cone is about 10 y ft, so the work done lifting the slab is about<br />
ΔW 57 p<br />
10 yy<br />
4<br />
2 Δy ft • lb.<br />
The work done lifting all the slabs from y 0 to y 8 to the rim is approximately<br />
W 57 p<br />
10 y y<br />
4<br />
2 Δy ft • lb.<br />
continued