5128_Ch07_pp378-433

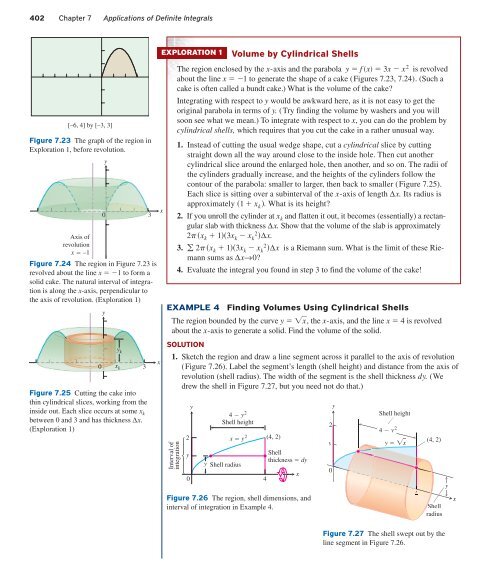
402 Chapter 7 Applications of Definite Integrals
[–6, 4] by [–3, 3]
Figure 7.23 The graph of the region in
Exploration 1, before revolution.
Axis of
revolution
x –1
Figure 7.24 The region in Figure 7.23 is
revolved about the line x 1 to form a
solid cake. The natural interval of integration
is along the x-axis, perpendicular to
the axis of revolution. (Exploration 1)
0
y
y
0 x k
y k
Figure 7.25 Cutting the cake into
thin cylindrical slices, working from the
inside out. Each slice occurs at some x k
between 0 and 3 and has thickness Δx.
(Exploration 1)
3
3
x
EXPLORATION 1
x
Volume by Cylindrical Shells
The region enclosed by the x-axis and the parabola y f x 3x x 2 is revolved
about the line x 1 to generate the shape of a cake (Figures 7.23, 7.24). (Such a
cake is often called a bundt cake.) What is the volume of the cake?
Integrating with respect to y would be awkward here, as it is not easy to get the
original parabola in terms of y. (Try finding the volume by washers and you will
soon see what we mean.) To integrate with respect to x, you can do the problem by
cylindrical shells, which requires that you cut the cake in a rather unusual way.
1. Instead of cutting the usual wedge shape, cut a cylindrical slice by cutting
straight down all the way around close to the inside hole. Then cut another
cylindrical slice around the enlarged hole, then another, and so on. The radii of
the cylinders gradually increase, and the heights of the cylinders follow the
contour of the parabola: smaller to larger, then back to smaller (Figure 7.25).
Each slice is sitting over a subinterval of the x-axis of length Δx. Its radius is
approximately 1 x k . What is its height?
2. If you unroll the cylinder at x k and flatten it out, it becomes (essentially) a rectangular
slab with thickness Δx. Show that the volume of the slab is approximately
2px k 13x k x 2 k Δx.
3. 2px k 13x k x 2 k Δx is a Riemann sum. What is the limit of these Riemann
sums as Δx→0?
4. Evaluate the integral you found in step 3 to find the volume of the cake!
EXAMPLE 4
Finding Volumes Using Cylindrical Shells
The region bounded by the curve y x, the x-axis, and the line x 4 is revolved
about the x-axis to generate a solid. Find the volume of the solid.
SOLUTION
1. Sketch the region and draw a line segment across it parallel to the axis of revolution
(Figure 7.26). Label the segment’s length (shell height) and distance from the axis of
revolution (shell radius). The width of the segment is the shell thickness dy. (We
drew the shell in Figure 7.27, but you need not do that.)
Interval of
integration
y
4 y 2
Shell height
2
x y 2 (4, 2)
⎧
⎪
y
Shell
⎨
thickness dy
⎪ y Shell radius
⎩
x
0 4
Figure 7.26 The region, shell dimensions, and
interval of integration in Example 4.
2
y
0
y
Shell height
4 y 2
y x
(4, 2)
Shell
radius
Figure 7.27 The shell swept out by the
line segment in Figure 7.26.
y
x