5128_Ch07_pp378-433

394 Chapter 7 Applications of Definite Integrals
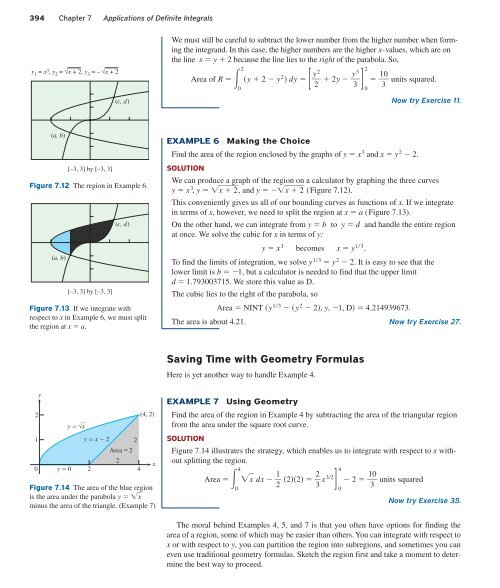
y 1 = x 3 , y 2 = √x + 2, y 3 = – √x + 2
(c, d)
We must still be careful to subtract the lower number from the higher number when forming
the integrand. In this case, the higher numbers are the higher x-values, which are on
the line x y 2 because the line lies to the right of the parabola. So,
Area of R 2
0
y 2 y 2 dy
[ y 2y y 2 3
2
3
]
2
1 0
units squared.
3
0
Now try Exercise 11.
(a, b)
[–3, 3] by [–3, 3]
Figure 7.12 The region in Example 6.
(a, b)
[–3, 3] by [–3, 3]
(c, d)
Figure 7.13 If we integrate with
respect to x in Example 6, we must split
the region at x a.
EXAMPLE 6
Making the Choice
Find the area of the region enclosed by the graphs of y x 3 and x y 2 2.
SOLUTION
We can produce a graph of the region on a calculator by graphing the three curves
y x 3 , y x 2, and y x 2 (Figure 7.12).
This conveniently gives us all of our bounding curves as functions of x. If we integrate
in terms of x, however, we need to split the region at x a (Figure 7.13).
On the other hand, we can integrate from y b to y d and handle the entire region
at once. We solve the cubic for x in terms of y:
y x 3 becomes x y 13 .
To find the limits of integration, we solve y 13 y 2 2. It is easy to see that the
lower limit is b 1, but a calculator is needed to find that the upper limit
d 1.793003715. We store this value as D.
The cubic lies to the right of the parabola, so
Area NINT y 13 y 2 2, y, 1, D 4.214939673.
The area is about 4.21. Now try Exercise 27.
Saving Time with Geometry Formulas
Here is yet another way to handle Example 4.
2
1
0
y
y 0
y √⎯x
y x 2 2
Area 2
2
2
4
(4, 2)
Figure 7.14 The area of the blue region
is the area under the parabola y x
minus the area of the triangle. (Example 7)
x
EXAMPLE 7
Using Geometry
Find the area of the region in Example 4 by subtracting the area of the triangular region
from the area under the square root curve.
SOLUTION
Figure 7.14 illustrates the strategy, which enables us to integrate with respect to x without
splitting the region.
Area x32]
4
x dx 1 4
2 22 2 2 1 0
units squared
3 3
0
0
Now try Exercise 35.
The moral behind Examples 4, 5, and 7 is that you often have options for finding the
area of a region, some of which may be easier than others. You can integrate with respect to
x or with respect to y, you can partition the region into subregions, and sometimes you can
even use traditional geometry formulas. Sketch the region first and take a moment to determine
the best way to proceed.