5128_Ch07_pp378-433

More documents

Recommendations

Info

Section 7.2 Areas in the Plane 393 While it appears that no single integral can give the area of R (the bottom boundary is defined by two different curves), we can split the region at x 2 into two regions A and B. The area of R can be found as the sum of the areas of A and B. Area of R 2 x dx 4 x x 2 dx 0 2 x32] area of A area of B 2 2 3 [ 2 3 x32 x 4 2 2 2x] 0 2 1 0 units squared 3 Now try Exercise 9. Integrating with Respect to y Sometimes the boundaries of a region are more easily described by functions of y than by functions of x. We can use approximating rectangles that are horizontal rather than vertical and the resulting basic formula has y in place of x. For regions like these y y y d x f(y) d x f(y) d x g(y) x f(y) x g(y) c x g(y) c 0 c x 0 x 0 x use this formula d A = ∫ [f (y) – g(y)]dy. 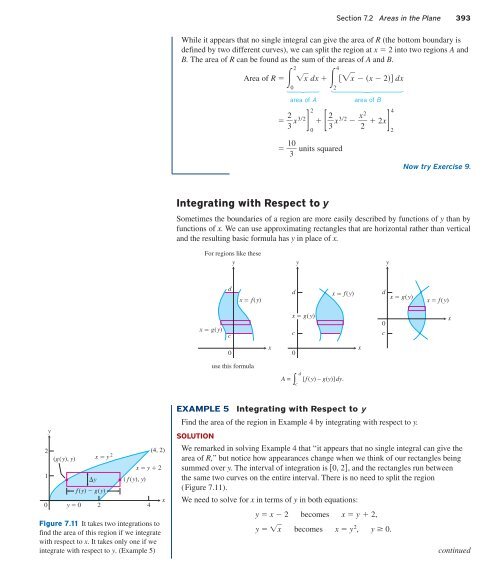c 2 1 0 y (g(y), y) y 0 y f(y) g(y) x y 2 (4, 2) ( f (y), y) x y 2 2 4 Figure 7.11 It takes two integrations to find the area of this region if we integrate with respect to x. It takes only one if we integrate with respect to y. (Example 5) x EXAMPLE 5 Integrating with Respect to y Find the area of the region in Example 4 by integrating with respect to y. SOLUTION We remarked in solving Example 4 that “it appears that no single integral can give the area of R,” but notice how appearances change when we think of our rectangles being summed over y. The interval of integration is 0, 2, and the rectangles run between the same two curves on the entire interval. There is no need to split the region (Figure 7.11). We need to solve for x in terms of y in both equations: y x 2 becomes x y 2, y x becomes x y 2 , y 0. continued
394 Chapter 7 Applications of Definite Integrals y 1 = x 3 , y 2 = √x + 2, y 3 = – √x + 2 (c, d) We must still be careful to subtract the lower number from the higher number when forming the integrand. In this case, the higher numbers are the higher x-values, which are on the line x y 2 because the line lies to the right of the parabola. So, Area of R 2 0 y 2 y 2 dy [ y 2y y 2 3 2 3 ] 2 1 0 units squared. 3 0 Now try Exercise 11. (a, b) [–3, 3] by [–3, 3] Figure 7.12 The region in Example 6. (a, b) [–3, 3] by [–3, 3] (c, d) Figure 7.13 If we integrate with respect to x in Example 6, we must split the region at x a. EXAMPLE 6 Making the Choice Find the area of the region enclosed by the graphs of y x 3 and x y 2 2. SOLUTION We can produce a graph of the region on a calculator by graphing the three curves y x 3 , y x 2, and y x 2 (Figure 7.12). This conveniently gives us all of our bounding curves as functions of x. If we integrate in terms of x, however, we need to split the region at x a (Figure 7.13). On the other hand, we can integrate from y b to y d and handle the entire region at once. We solve the cubic for x in terms of y: y x 3 becomes x y 13 . To find the limits of integration, we solve y 13 y 2 2. It is easy to see that the lower limit is b 1, but a calculator is needed to find that the upper limit d 1.793003715. We store this value as D. The cubic lies to the right of the parabola, so Area NINT y 13 y 2 2, y, 1, D 4.214939673. The area is about 4.21. Now try Exercise 27. Saving Time with Geometry Formulas Here is yet another way to handle Example 4. 2 1 0 y y 0 y √⎯x y x 2 2 Area 2 2 2 4 (4, 2) Figure 7.14 The area of the blue region is the area under the parabola y x minus the area of the triangle. (Example 7) x EXAMPLE 7 Using Geometry Find the area of the region in Example 4 by subtracting the area of the triangular region from the area under the square root curve. SOLUTION Figure 7.14 illustrates the strategy, which enables us to integrate with respect to x without splitting the region. Area x32] 4 x dx 1 4 2 22 2 2 1 0 units squared 3 3 0 0 Now try Exercise 35. The moral behind Examples 4, 5, and 7 is that you often have options for finding the area of a region, some of which may be easier than others. You can integrate with respect to x or with respect to y, you can partition the region into subregions, and sometimes you can even use traditional geometry formulas. Sketch the region first and take a moment to determine the best way to proceed.
Page 1 and 2: Chapter7 Applications of Definite I
Page 3 and 4: 380 Chapter 7 Applications of Defin
Page 15: 392 Chapter 7 Applications of Defin

5128_Ch07_pp378-433

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?