Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
Section 7.2 Areas in the Plane 391<br />
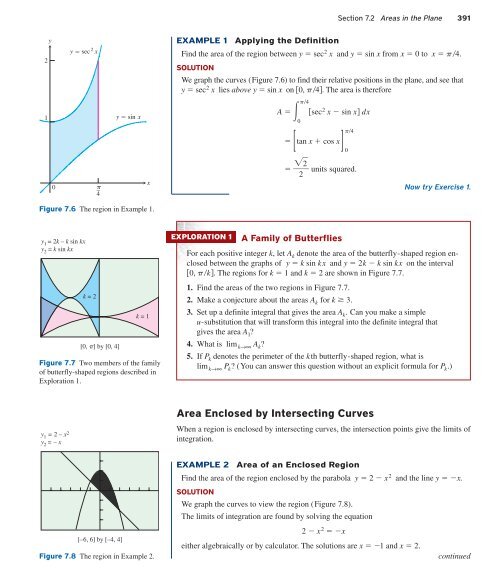
y<br />
2<br />
y sec 2 x<br />
EXAMPLE 1<br />
Applying the Definition<br />
Find the area of the region between y sec 2 x and y sin x from x 0 to x p4.<br />
SOLUTION<br />
We graph the curves (Figure 7.6) to find their relative positions in the plane, and see that<br />
y sec 2 x lies above y sin x on 0, p4. The area is therefore<br />
1<br />
y sin x<br />
A p4<br />
sec 2 x sin x dx<br />
0<br />
p4<br />
<br />
[ ]<br />
tan x cos x 0<br />
2<br />
units squared.<br />
2<br />
0<br />
–4<br />
x<br />
Now try Exercise 1.<br />
Figure 7.6 The region in Example 1.<br />
y 1 = 2k – k sin kx<br />
y 2 = k sin kx<br />
k = 2<br />
[0, ] by [0, 4]<br />
k = 1<br />
Figure 7.7 Two members of the family<br />
of butterfly-shaped regions described in<br />
Exploration 1.<br />
EXPLORATION 1<br />
A Family of Butterflies<br />
For each positive integer k, let A k denote the area of the butterfly-shaped region enclosed<br />
between the graphs of y k sin kx and y 2k k sin kx on the interval<br />
0, pk. The regions for k 1 and k 2 are shown in Figure 7.7.<br />
1. Find the areas of the two regions in Figure 7.7.<br />
2. Make a conjecture about the areas A k for k 3.<br />
3. Set up a definite integral that gives the area A k . Can you make a simple<br />
u-substitution that will transform this integral into the definite integral that<br />
gives the area A 1 ?<br />
4. What is lim k→∞ A k ?<br />
5. If P k denotes the perimeter of the kth butterfly-shaped region, what is<br />
lim k→∞ P k ? (You can answer this question without an explicit formula for P k .)<br />
y 1 = 2 – x 2<br />
y 2 = – x<br />
[–6, 6] by [–4, 4]<br />
Figure 7.8 The region in Example 2.<br />
Area Enclosed by Intersecting Curves<br />
When a region is enclosed by intersecting curves, the intersection points give the limits of<br />
integration.<br />
EXAMPLE 2<br />
Area of an Enclosed Region<br />
Find the area of the region enclosed by the parabola y 2 x 2 and the line y x.<br />
SOLUTION<br />
We graph the curves to view the region (Figure 7.8).<br />
The limits of integration are found by solving the equation<br />
2 x 2 x<br />
either algebraically or by calculator. The solutions are x 1 and x 2.<br />
continued