5128_ch04ansTE_pp652-661

652 Additional Answers
31. Maximum value is 11 at x 5;
minimum value is 5 on the interval [3, 2];
local maximum at (5, 9)
32. Maximum value is 4 on the interval [5, 7];
minimum value is 4 on the interval [2, 1].
33. Maximum value is 5 on the interval [3, );
minimum value is 5 on the interval (, 2].
34. Minimum value is 4 on the interval [1, 3].
35. crit. pt. derivative extremum value
x 4 5 0 local max 1 2
10 1/3 1.034
25
x 0 undefined local min 0
36.
crit. pt. derivative extremum value
x 1 0 minimum 3
x 0 undefined local max 0
x 1 0 minimum 3
37.
crit. pt. derivative extremum value
x 2 undefined local max 0
x 2 0 minimum 2
x 2 0 maximum 2
x 2 undefined local min 0
38. crit. pt. derivative extremum value
x 0 0 minimum 0
x 1 2
0 local max 1 44
15 1/2 4.462
5
125
x 3 undefined minimum 0
39. crit. pt. derivative extremum value
x 1 undefined minimum 2
40. crit. pt. derivative extremum value
x 0 undefined local min 3
x 1 0 local max 4
41. crit. pt. derivative extremum value
x 1 0 maximum 5
x 1 undefined local min 1
x 3 0 maximum 5
42.
crit. pt. derivative extremum value
x 1 0 local max 4
x 3.155 0 local max 3.079
46. False. Consider the graph below.
y
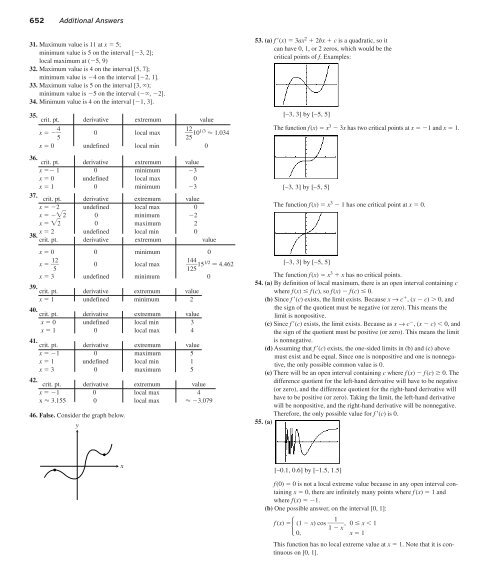
53. (a) f (x) 3ax 2 2bx c is a quadratic, so it
can have 0, 1, or 2 zeros, which would be the
critical points of f. Examples:
[–3, 3] by [–5, 5]
The function f(x) x 3 3x has two critical points at x 1 and x 1.
[–3, 3] by [–5, 5]
The function f(x) x 3 1 has one critical point at x 0.
[–3, 3] by [–5, 5]
The function f(x) x 3 x has no critical points.
54. (a) By definition of local maximum, there is an open interval containing c
where f(x) f(c), so f(x) f(c) 0.
(b) Since f (c) exists, the limit exists. Because x → c ,(x c) 0, and
the sign of the quotient must be negative (or zero). This means the
limit is nonpositive.
(c) Since f (c) exists, the limit exists. Because as x → c ,(x c) 0, and
the sign of the quotient must be positive (or zero). This means the limit
is nonnegative.
(d) Assuming that f(c) exists, the one-sided limits in (b) and (c) above
must exist and be equal. Since one is nonpositive and one is nonnegative,
the only possible common value is 0.
(e) There will be an open interval containing c where f (x) f (c) 0. The
difference quotient for the left-hand derivative will have to be negative
(or zero), and the difference quotient for the right-hand derivative will
have to be positive (or zero). Taking the limit, the left-hand derivative
will be nonpositive, and the right-hand derivative will be nonnegative.
Therefore, the only possible value for f (c) is 0.
55. (a)
x
[–0.1, 0.6] by [–1.5, 1.5]
f(0) 0 is not a local extreme value because in any open interval containing
x 0, there are infinitely many points where f (x) 1 and
where f(x) 1.
(b) One possible answer, on the interval [0, 1]:
f (x)
(1 x) cos 1
, 0 x 1
1 x
0, x 1
This function has no local extreme value at x 1. Note that it is continuous
on [0, 1].

Additional Answers 653
Section 4.2
Exercises 4.2
11. Because the trucker’s average speed was 79.5 mph, and by the Mean Value
Theorem, the trucker must have been going that speed at least once during
the trip.
12. Let f (t) denote the temperature indicated after t seconds. We assume that
f (t) is defined and continuous for 0 t 20. The average rate of change
is 10.6°F/sec. Therefore, by the Mean Value Theorem, f (c) 10.6°F/sec
for some value of c in [0, 20].
13. Because its average speed was approximately 7.667 knots, and by the
Mean Value Theorem, it must have been going that speed at least once
during the trip.
14. The runner’s average speed for the marathon was approximately 11.909 mph.
Therefore, by the Mean Value Theorem, the runner must have been going
that speed at least once during the marathon. Since the initial speed and
final speed are both 0 mph and the runner’s speed is continuous, by the
Intermediate Value Theorem, the runner’s speed must have been 11 mph
at least twice.
25. (a) Local max at (2, 1/4);
local min at (2, 1/4)
(b) On (, 2] and [2, )
(c) On [2, 2]
26. (a) None (b) None
(c) On (, 2), (2, 2), and (2, )
27. (a) Local maximum at (1.126, 0.036);
local minimum at (0.559, 2.639)
(b) On (, 1.126] and [0.559, )
(c) On [1.126, 0.559]
39. Possible answers:
(a)
(b)
(c)
(d)
41. One possible answer:
[–3, 3] by [–15, 15]
42. One possible answer:
[–2, 4] by [–2, 4]
(b)
(c)
[–1, 4] by [0, 3.5]
[–1, 4] by [0, 3.5]
40. Possible answers:
(a)
46. Because the Mean Value Theorem applies to the function y sin x on any
interval, and y cos x is the derivative of sin x. So, between any two zeros
of sin x, its derivative, cos x, must be zero at least once.
47. f(x) must be zero at least once between a and b by the Intermediate Value
Theorem.
Now suppose that f (x) is zero twice between a and b. Then by the Mean
Value Theorem, f (x) would have to be zero at least once between the two
zeros of f(x), but this can’t be true since we are given that f (x) 0 on this
interval.
Therefore, f(x) is zero once and only once between a and b.
48. Let f(x) x 4 3x 1. Then f(x) is continuous and differentiable everywhere.
f (x) 4x 3 3, which is never zero between x 2 and x 1.
Since f (2) 11 and f (1) 1, exercise 47 applies, and f(x) has exactly
one zero between x 2 and x 1.
49. Let f(x) x ln (x 1). Then f(x) is continuous and differentiable
1
everywhere on [0, 3]. f (x) 1 , which is never zero on [0, 3].
x 1
Now f(0) 0, so x 0 is one solution of the equation. If there were a
second solution, f(x) would be zero twice in [0, 3], and by the Mean Value
Theorem, f (x) would have to be zero somewhere between the two zeros
of f(x). But this can’t happen, since f (x) is never zero on [0, 3]. Therefore,
f(x) 0 has exactly one solution in the interval [0, 3].
50. Consider the function k(x) f(x) g(x). k(x) is continuous and differentiable
on [a, b], and since k(a) f(a) g(a) 0 and

654 Additional Answers
k(b) f(b) g(b) 0, by the Mean Value Theorem, there must be a point
c in (a, b) where k(c) 0. But since k(c) f (c) g(c), this means
that f (c) g(c), and c is a point where the graphs of f and g have parallel
or identical tangent lines.
Section 4.3
Exercises 4.3
may vary.
(a) y
(b)
may vary.
2898438
(a) y 1 49.
252
(b)
b a
51. False. For example, the function x 3 is increasing on (1, 1), but f(0) 0.
52. True. In fact, f is increasing on [a, b] by Corollary 1 to the Mean Value
Theorem.
57. (a) Increasing: [2, 1.3] and [1.3, 2];
decreasing: [1.3, 1.3];
local max: x 1.3
local min: x 1.3
(b) Regression equation: y 3x 2 5
(c) f(x) x 3 5x
[–2.5, 2.5] by [–8, 10]
58. (a) Toward: 0 t 2 and 5 t 8;
away: 2 t 5
(b) A local extremum in this problem is a time/place where Priya changes
the direction of her motion.
(c) Regression equation:
y 0.0820x 3 0.9163x 2 2.5126x 3.3779
(d) f(t) 0.2459t 2 1.8324t 2.5126
toward: 0 t 1.81 and 5.64 t 8;
away: 1.81 t 5.64
59. f(b 1 ) f(a)
b 1 a
1
b a
a b
1 1 1
f (c) c 2, so c 2 and c 2 ab.
a b
Thus, c ab.
60. f(b ) f(a)
b
a
b2 a2
b b a
a
f (c) 2c, so2c b a and c a b
.
2
61. By the Mean Value Theorem, sin b sin a (cos c)(b a) for some c
between a and b. Taking the absolute value of both sides and using
⏐cos c⏐ 1 gives the result.
62. Apply the Mean Value Theorem to f on [a, b].
Since f(b) f (a), f (b ) f(a)
is negative, and hence f (x) must be negative
at some point between a and b.
b
a
63. Let f(x) be a monotonic function defined on an interval D. For any two
values in D, we may let x 1 be the smaller value and let x 2 be the larger
value, so x 1 x 2 . Then either f(x 1 ) f(x 2 ) (if f is increasing), or
f(x 1 ) f(x 2 ) (if f is decreasing), which means f(x 1 ) f(x 2 ). Therefore, f is
one-to-one.
25. (a) v(t) 2t 4 (b) a(t) 2
(c) It begins at position 3 moving in a negative direction. It moves to position
1 when t 2, and then changes direction, moving in a positive
direction thereafter.
26. (a) v(t) 2 2t (b) a(t) 2
(c) It begins at position 6 and moves in the negative direction thereafter.
27. (a) v(t) 3t 2 3 (b) a(t) 6t
(c) It begins at position 3 moving in a negative direction. It moves to position
1 when t 1, and then changes direction, moving in a positive direction
thereafter.
28. (a) v(t) 6t 6t 2 (b) a(t) 6 12t
(c) It begins at position 0. It starts moving in the positive direction until it
reaches position 1 when t 1, and then it changes direction. It moves
in the negative direction thereafter.
31. Some calculators use different logistic regression equations, so answers
12655.179
1 12.871e 0.0326x
[0, 140] by [–200, 12000]
(c) The regression equation predicts a population of 12,209,870. (This is
remarkably close to the 2000 census number of 12,281,054.)
(d) The second derivative has a zero at about 78, indicating that the population
was growing the fastest in 1898. This corresponds to the inflection
point on the regression curve.
(e) The regression equation predicts a population limit of about
12,655,179.
32. Some calculators use different logistic regression equations, so answers
6.
288
e
0.
851x
[0, 9] by [–3.1 10 6 , 3.2 10 7 ]
(c) The zero of the second derivative is about 4.6, which puts the fastest
growth during 1981. This corresponds to the inflection point of the regression
curve.
(d) The regression curve predicts that cable subscribers will approach a
limit of 28,984,386 12,168,450 subscribers (about 41 million).
(e) For many reasons, the potential market for cable TV subscribers between
1977 and 1985 was limited compared to today. Some reasons are: the
technology has improved, televisions have become cheaper, there are
more cable stations to entice viewers, and many more communities
have access to cable.
33. y3 3x 2 and y6x.
y0 at 1. y(1) 0 and y(1) 0, so there is a local minimum at
(1, 3) and a local maximum at (1, 7).
34. y5x 4 80 and y20x 3 .
y0 at 2. y(2) 0 and y(2) 0, so there is a local maximum at
(2, 228) and a local minimum at (2, 28).

Additional Answers 655
35. y3x 2 6x and y6x 6.
y0 at 2 and 0. y(2) 0 and y(0) 0, so there is a local maximum
at (– 2, 2) and a local minimum at (0, 2).
36. y15x 4 75x 2 60 and y60x 3 150x.
y0 at 1 and 2. y(2) 0, y(1) 0, y(1) 0, and y(2) 0;
so there are local maxima at (2, 4) and (1, 58), and there are local
minima at (1, 18) and (2, 36).
37. y(x 1)e x and y(x 2)e x .
y0 at 1 and y(1) 0 , so there is a local minimum at (1, 1/e).
38. y(1 x)e x and y(x 2)e x .
y0 at 1 and y(1) 0, so there is a local maximum at (1, 1e)
41.
y
y = f′(x)
y = f(x)
P
47. One possible answer:
y
(–2, 8) 10
(0, 4)
–5
(2, 0)
–10
48. One possible answer:
5
x
x
y = f′′(x)
42.
43. No. f must have a horizontal tangent line at that point, but it could be increasing
(or decreasing) on both sides of the point, and there would be no
local extremum.
44. No. f (x) could still be positive (or negative) on both sides of x c, in
which case the concavity of the function wouldn’t change at x c.
45. One possible answer:
y
–5
5
5
x
51. (a) Absolute maximum at (1, 2);
absolute minimum at (3, 2)
(b) None
(c) One possible answer:
2
1
–1
–2
y
1
y = f(x)
52. (a) Absolute maximum at (0, 2);
absolute minimum at (2, 1) and (2, 1)
(b) At (1, 0) and (1, 0)
(c) One possible answer:
2
3
x
–5
46. One possible answer:
(d) f(3) f(3), and 1 f(3) 0.

656 Additional Answers
53.
y
4
3
2
1
y = f(x)
By the First Derivative test, f has relative minima at x 1 and x 4
and relative maxima at x 2.
(b) f (x) 6(x2 )
(x
2 2 2x(6x)
2) 2 6(x
2 2)
(x 2 .
2) 2 Since f changes sign at
x 2, there are points of inflection at x 2 .
(c) Comparing the two relative maxima, we see that f(2) 3 ln 6 4
and f(2) 3ln 6 4. The absolute maximum is 3 ln 6 4.
54.
–1
1
2
3
4
5
6
x
Section 4.4
Exercises 4.4
18. (a) V(x) 2x 3 25x 2 75x
(b) Domain: (0, 5)
61. (a) In Exercise 7, a 4 and b 21,
b
so 7 ,which is the x-value where the point of inflection occurs.
3 a 4
The local extrema are at x 2 and x 3 ,which are symmetric
2
about x 7 4 .
b
(b) In exercise 2, a 2 and b 6, so 1, which is the x-value
3 a
where the point of inflection occurs. The local extrema are at x 0 and
x 2, which are symmetric about x 1.
(c) f (x) 3ax 2 2bx c and f (x) 6ax 2b.
The point of inflection will occur where f (x) 0, which is at
b
x .
3 a
If there are local extrema, they will occur at the zeros of f (x). since
f (x) is quadratic, its graph is a parabola and any zeros will be
symmetric about the vertex which will also be where f (x) 0.
abce 62. (a) f (x) b x
(e bx
,
a) 2 so the sign of f (x) is the
same as the sign of the product abc.
(b) f (x) ab2 ceb
x ( e bx a)
( e bx
.
a)
3 Since a 0, this changes sign
when x ln a
due to the e bx a factor in the numerator, and
b
there is a point of inflection at that location.
63. (a) Since f (x) is quadratic it must have 0, 1, or 2 zeros. If f (x) has 0 or 1
zeros, it will not change sign and the concavity of f(x) will not change,
so there is no point of inflection. If f (x) has 2 zeros, it will change
sign twice, and f(x) will have 2 points of inflection.
(b) f(x) has two points of inflection if and only if 3b 2 8ac.
Quick Quiz (Sections 4.1–4.3)
6x
4. (a) f(x) x 2 2 2(x 1)( x 2)
2
x 2 . Critical numbers are x 1
2
and x 2. The sign graph of f is shown below.
–2 1 2 4
x
(c) Maximum volume 66.02 in 3 when x 1.96 in.
(d) V (x) 6x 2 50x 75, so the critical point is at x 25 57
,
6
which confirms the result in part (c).
19. (a) V(x) 2x(24 2x)(18 2x)
(b) Domain: (0, 9)
[0, 9] by [–400, 1600]
(c) Maximum volume 1309.95 in 3 when x 3.39 in.
(d) V(x) 24x 2 336x 864, so the critical point is at x 7 13,
which confirms the result in part (c).
(e) x 2 in. or x 5 in.
(f) The dimensions of the resulting box are 2x in., (24 2x) in.,
and (18 2x) in. Each of these measurements must be positive, so that
gives the domain of (0, 9).
22. Dimensions: Radius 10
2 3 20
8.16 cm, height 11.55 cm;
3
4000
maximum volume 2418.40 cm 3
33
23. Set r(x) c(x): 4x 1/2 4x. The only positive critical value is x 1, so
profit is maximized at a production level of 1000 units. Note that
(r c)(x) 2(x) 3/2 4 0 for all positive x, so the Second Derivative
Test confirms the maximum.
24. Set r(x) c(x): 2x/(x 2 1) 2 (x 1) 2 . We solve this equation graphically
to find that x 0.294 or x 1.525. The graph of y r(x) c(x)
shows a minimum at x 0.294 and a maximum at x 1.525, so profit is
maximized at a production level of about 1,525 units.
25. Set c(x) c(x)/x:3x 2 20x 30 x 2 10x 30. The only positive
solution is x 5, so average cost is minimized at a production level of
d 2
5000 units. Note that d x2 c( x) 2 0 for all positive x, so the Second
x
Derivative Test confirms the minimum.
26. Set c(x) c(x) /x: xe x e x 4x e x 2x. The only positive solution is
x ln 2, so average cost is minimized at a production level of 1000 ln 2,
d 2
which is about 693 units. Note that d x2
c( x)
x
e x 0 for all positive x,
so the Second Derivative Test confirms the minimum.

Additional Answers 657
28. (a) At x 1
(b) a b A
0.1 3.72 0.33
0.2 2.86 0.44
0.3 2.36 0.46
0.4 2.02 0.43
0.5 1.76 0.38
0.6 1.55 0.31
0.7 1.38 0.23
0.8 1.23 0.15
0.9 1.11 0.08
1.0 1.00 0.00
(c)
(c)
Changing the value of k changes the maximum strength, but not the
dimensions of the strongest beam. The graphs for different values of k
look the same except that the vertical scale is different.
38. (a) 6 in. wide by 63 in. deep
(b)
[0, 1.1] by [–0.2, 0.6]
(d) Quadratic:
A 0.91a 2 0.54a 0.34
(c)
[0, 12] by [–2000, 8000]
[0, 12] by [–2000, 8000]
[–0.5, 1.5] by [–0.2, 0.6]
Cubic:
A 1.74a 3 3.78a 2 1.86a 0.19
y x 3 (144 x 2 ) 1/2
Changing the value of k changes the maximum stiffness, but not the dimensions
of the stiffest beam. The graphs for different values of k look
the same except that the vertical scale is different.
39. (a) Maximum speed 10 cm/sec;
maximum speed is at t 1 2 , 3 2 , 5 2 , 7 2 seconds;
[–0.5, 1.5] by [–0.2, 0.6]
Quartic:
A 1.92a 4 5.96a 3 6.87a 2 2.71a 0.12
[–0.5, 1.5] by [–0.2, 0.6]
(e) Quadratic: A 0.42;
cubic: A 0.45;
quartic: A 0.46
37. (a) 43 in. wide by 46 in. deep
(b)
position at those times is s 0 cm (rest position);
acceleration at those times is 0 cm/sec 2
(b) The magnitude of the acceleration is greatest
when the cart is at positions s 10 cm;
The speed of the cart is 0 cm/sec at those times.
57. Let P be the foot of the perpendicular from A to the mirror, and Q be the
foot of the perpendicular from B to the mirror. Suppose the light strikes the
mirror at point R on the way from A to B. Let:
a distance from A to P
b distance from B to Q
c distance from P to Q
x distance from P to R
To minimize the time is to minimize the total distance the light travels
going from A to B. The total distance is
D(x) (x 2 a 2 ) 1/2 ((c x) 2 b 2 ) 1/2 .
Then D(x) 0 and D(x) has it minimum when
ac
x c
x , or, a . It follows that
a b a b
bc
c x , or c x c
. This means that the two triangles APR
a b b a b
and BQR are similar, and the two angles must be equal.
59. (a) d v
cr(2r
dr
0 3r) which is zero when
r 2 3 r 0 .
(b)

658 Additional Answers
63. (a) y(0) 0 (b) y(L) 0
(c) y(0) 0, so d 0. y(0) 0, so c 0.
Then y(L) aL 3 bL 2 H and
y(L) 3aL 2 2bL 0.
H H
Solving, a 2 L 3 and b 3 L 2, which gives the equation shown.
64. (a) V(x) 3 2 a x
2
2 a2
a
2
x
2
2
(b) When a 4: r 4 6
, h 4 3
;
3 3
when a 5: r 5 6
, h 5 3
;
3 3
when a 6: r 26, h 23;
when a 8: r 8 6
, h 8 3
3 3
(c) h
r 2
a
65. (a) The x- and y-intercepts of the line through R and T are x and f (x)
a xf(x) respectively.
The area of the triangle is the product of these two values.
(b) Domain: (0, 10)
2. (a) L(x) 4 5 x 9 5
(b) Differs from the true value in absolute value by less than 10 3
3. (a) L(x) 2
(b) Differs from the true value in absolute value by less than 10 2
4. (a) L(x) x
(b) Differs from the true value in absolute value by less than 10 2
5. (a) L(x) x
(b) Differs from the true value in absolute value by less than 10 3
6. (a) L(x) x 2
(b) Differs from the true value in absolute value by less than 10 3
7. f(0) 1. Also, f (x) k(1 x) k1 , so f (0) k.
This means the linearization at x 0 is L(x) 1 kx.
19. (a) dy (3x 2 3) dx
(b) dy 0.45 at the given values
2 2x2
20. (a) dy (1 x2) 2 dx
(b) dy 0.024 at the given values
21. (a) dy (2x ln x x) dx
(b) dy 0.01 at the given values
1 2x2
22. (a) dy (1 x2) 1 /2 dx
(b) dy 0.2 at the given values
23. (a) dy (cos x) e sin x dx
(b) dy 0.1 at the given values
24. (a) dy csc 1 3
x
cot 1 3
x
dx
The vertical asymptotes at x 0 and x 10 correspond to horizontal
or vertical tangent lines, which do not form triangles.
(c) Height 15, which is 3 times the y-coordinate of the center of the
ellipse.
(d) Part (a) remains unchanged.
The domain is (0, C) and the graph is similar.
The minimum area occurs when x 2 3C 2
. From this, it follows that
4
the triangle has minimum area when its height is 3B.
Section 4.5
Quick Review 4.5
9.
10.
[0, 10] by [–100, 1000]
[0, π] by [–0.2, 1.3]
(b) dy 0.205525 at the given values
25. (a) dy (x
dx1) 2
(b) dy 0.01 at the given values
x y
26. (a) dy 2 2 x
dx
(b) dy 0.0375 at the given values
53. Since V 4 3 r3 , we have dV 4r 2 dr 4r 2 1
16
r 2
.
4
The volume error in each case is simply r 2
in 3 .
4
Sphere Type True Radius Tape Error Radius Error Volume Error
Orange 2" 1/8" 1/16 " 1 in 3
Melon 4" 1/8" 1/16 " 4 in 3
Beach Ball 7" 1/8" 1/16 " 12.25 in 3
54. Since A 4r 2 1 r
, we have dA 8rdr 8r
16
. 2
The surface area error in each case is simply 2
r in 2 .
Sphere Type True Radius Tape Error Radius Error S. Area Error
Orange 2" 1/8" 1/16 " 1 in 2
Melon 4" 1/8" 1/16 " 2 in 2
Beach Ball 7" 1/8" 1/16 " 3.5 in 2
1
64. If x 1 h, then f(x 1 ) 2h 1/2 and x 2 h h 1/2
1
h 2h h. If x 1 h,
2h 1/2
1
then f(x 1 ) 2h 1/2 and x 2 h 2h h.
Exercises 4.5
1. (a) L(x) 10x 13
(b) Differs from the true value in absolute value by less than 10 1

Additional Answers 659
65. x 2 2, x 3 4, x 4 8, and x 5 16;
⏐x n ⏐ 2 n1 .
[–10, 10] by [–3, 3]
66. (a) b 0 f(a), b 1 f (a), and b 2 f (a)
.
2
(b) 1 x x 2
(c) As one zooms in, the two graphs quickly become indistinguishable.
They appear to be identical.
(d) The quadratic approximation is
1 (x 1) (x 1) 2 .
As one zooms in, the two graphs quickly become indistinguishable.
They appear to be identical.
(e) The quadratic approximation is
x x2
1 . 2 8
As one zooms in, the two graphs quickly become indistinguishable.
They appear to be identical.
(f) For f :1 x ;
for g:1 (x 1) 2 x;
x
for h:1 2
67. Finding a zero of sin x by Newton’s method would use the recursive formula
sin(
xn)
x n1 x n x c os(
xn)
n tan x n , and that is exactly what the calculator
would be doing. Any zero of sin x would be a multiple of p.
69. lim tan x
lim sin x/ cos x
x→0 x x→0 x
lim
x→0 1
sin x
cos x x
lim 1
x→0 cos x lim sin x
x→0 x
(1)(1) 1.
70. g(a) c, so if E(a) 0, then g(a) f(a) and
c f(a). Then
E(x) f(x) g(x) f(x) f(a) m(x a).
E(x)
Thus, f (x) f (a)
m.
x a x a
lim f(x ) f(a)
f (a), so if the limit of
x→a x a
E(x)
is zero, then m f (a) and g(x) L(x).
x a
Section 4.6
Exercises 4.6
45. (a) The point being plotted would correspond to a point on the edge of the
wheel as the wheel turns.
(b) One possible answer:
16pt, where t is in seconds.
(c) Assuming counterclockwise motion, the rates are as follows.
p 4 ; d x
71.086 ft/sec
dt
d y
71.086 ft/sec
dt
2 : d x
100.531 ft/sec
dt
d y
0 ft/sec
dt
p: d x
0 ft/sec
dt
d y
100.531 ft/sec
dt
46. (a) One possible answer:
x 30 cos , y 40 30 sin
(b) Assuming counterclockwise motion, the rates are as follows.
When t 5: d x
0 ft/sec
dt
d y
18.850 ft/sec
dt
when t 8: d x
17.927 ft/sec
dt
d y
5.825 ft/sec
dt
Quick Quiz (Sections 4.4–4.6)
4. (a) Since d y
1 1
dx
2 x1/2 , the slope at (25, 5) is . 1 0
1
The linearization is L(x) (x 25) 5, so L(26) 5.1.
1 0
f(
5)
(b) x 2 5 5 52 26
5.1.
f (
5)
2(5)
(c) The appropriate linearization is for the curve y 3 x at the point (27, 3).
Since d y
1 1
dx
3 x2/3 , the slope at (27, 3) is . The linearization is
2 7
1
L(x) (x 27) 3, so L(26) 3 – 1/27 2.963.
2 7
Review Exercises
5. (a) Approximately (, 0.385]
(b) Approximately [0.385, )
(c) None (d) (, )
(e) Local maximum at (0.385, 1.215)
(f) None
6. (a) [1, ) (b) (, 1]
(c) (, )
(d) None
(e) Local minimum at (1, 0)
(f ) None
7. (a) [0, 1) (b) (1, 0]
(c) (1, 1)
(d) None
(e) Local minimum at (0, 1)
(f) None
8. (a) (, 2 1/3 ] (, 0.794]
(b) [2 1/3 ,1) [0.794, 1) and (1, )
(c) (, 2 1/3 ) (, 1.260) and (1, )
(d) (1.260, 1)
(e) Local maximum at
21/3 , 2 3 21/3 (0.794, 0.529)
(f)
21/3 , 1 3 21/3 (1.260, 0.420)
9. (a) None (b) [1, 1]
(c) (1, 0) (d) (0, 1)
(e) Local maximum at (1, p);
local minimum at (1, 0)
(f)
0, p 2

660 Additional Answers
10. (a) [3, 3]
(e) Local maximum at (0.889, 1.011);
(b) (,3] and [3, )
local minimum at (0, 0)
(c) Approximately (2.584, 0.706) and (3.290, )
(f)
(d) Approximately (, 2.584) and (0.706, 3.290)
2 9 , 0.667
(e) Local maximum at
16. (a) Approximately (, 0.215]
3, (b) Approximately [0.215, 2) and (2, )
3 1
(1.732, 0.183);
(c) Approximately (2, 3.710)
4
(d) (, 2) and approximately (3.710, )
local minimum at
(e) Local maximum at (0.215, 2.417)
3,
(f) (3.710, 3.420)
(1.732, 0.683)
4
35. .
y
(f) (2.584, 0.573), (0.706, 0.338), and (3.290, 0.161)
2
11. (a) (0, 2] (b) [2, 0)
(c) None (d) (2, 0) and (0, 2)
(e) Local maxima at (2, ln 2) and (2, ln 2)
x
(f) None
–3
3
12. (a) Approximately [0, 0.176], 0.994, p 2 ,
y = f(x)
[2.148, 2.965],
3.834, 3 p
2 , and 5.591, 2p
(b) Approximately [0.176, 0.994], p 2 , 2.148 ,
p
[2.965, 3.834], and 3 , 5.591
2
(c) Approximately (0.542, 1.266), (1.876, 2.600),
(3.425, 4.281), and (5.144, 6.000)
(d) Approximately (0, 0.542), (1.266, 1.876),
(2.600, 3.425), (4.281, 5.144),
and (6.000, 2p)
(e) Local maxima at (0.176, 1.266), p 2 ,0
p
and (2.965, 1.266), 3 ,2
2
, and (2p, 1);
local minima at (0, 1),
(0.994, 0.513),
(2.148, 0.513), (3.834, 1.806),
and (5.591, 1.806)
Note that the local extrema at x 3.834,
x 3 p , and x 5.591 are also absolute extrema.
2
(f) (0.542, 0.437), (1.266, 0.267),
(1.876, 0.267), (2.600, 0.437), (3.425, 0.329), (4.281, 0.120),
(5.144, 0.120), and (6.000, 0.329)
2
13. (a) 0,
(b) (, 0] and
2
3
,
(c) (, 0) (d) (0, )
(e) Local maximum at
2 16
(1.155, 3.079)
3
3
3 1
, 33
(f ) None
14. (a) Approximately [0.578, 1.692]
(b) Approximately (, 0.578] and [1.692, )
(c) Approximately (, 1.079)
(d) Approximately (1.079, )
(e) Local maximum at (1.692, 20.517);
local minimum at (0.578, 0.972)
(f) (1.079, 13.601)
15. (a) 0, 8 9
(b) (, 0] and
8 , )
9
(c)
, 2 9
(d) 2 9 ,0
and (0, )
–3
36. (a) Absolute minimum is 2 at x 1;
absolute maximum is 3 at x 3
(b) None
(c)
1633001.59
41. (a) With some rounding, y
1 17.471e 0.06378t
(b) The regression fit looks very good:
[0, 80] by [0, 1600000]
(c) 1,476,128 829,210 2,305,337
(d) About 1885; the graph has an inflection at this point.
(e) The maximum population will be about 2,462,000.
(f) There are many possible causes. Advances in transportation began
drawing the population southward after 1920, and Tennessee was wellsituated
geographically to become a crossroads of river, railroad, and
automobile routes. By the year 2000 there had been numerous other
demographic changes. It should also be pointed out that the census
years in the data (1850 – 1910) include the years of the Civil War and
Reconstruction, so the regression is based on unusual data to begin with.
51. (a) V(x) x(15 – 2x)(5 – x)
(b) 0 x 5
[0, 5] by [10, 70]

Additional Answers 661
(c) Maximum volume 66.019 in 3 when x 1.962 in.
(d) V(x) 6x 2 – 50 x 75 which is zero at x 25 57
1.962.
6
(b)
y
2
70. (a) The only x-value for which f has a relative maximum is x – 2. That
is the only place where the derivative of f goes from positive to
negative.
(b) The only x-value for which f has a relative minimum is x 0. That is
the only place where the derivative of f goes from negative to positive.
(c) The graph of f is concave up on (1, 1) and on (2, 3). Those are the intervals
on which the derivative of f is increasing.
(d)
y
LRAM 1.25
2
x
6. (a)
2
y
–3 3
x
72. (a) V a 2 b, and b 60 2a
15 a 4
2 , so V 15pa2 p a 3 .
2
Thus d V
30pa 3p a 2
3 pa(20 a). The domain of consideration
da
2 2
for a in this problem is (0, 30), so a 20 is the only critical number.
The cylinder of maximum volume is formed when a 20 and b 5.
(b) The sign graph for the derivative d V
3 pa(20 – a) on the interval
da
2
(0, 30) is as follows:
x
0 20 30
By the First Derivative Test, there is a maximum at x 20.
(b)
2
y
RRAM 1.25
2
x
CHAPTER 5
2
x
Section 5.1
Exercises 5.1
5. (a) y
2
7.
MRAM 1.375
n LRAM n MRAM n RRAM n
10 1.32 1.34 1.32
50 1.3328 1.3336 1.3328
100 1.3332 1.3334 1.3332
500 1.333328 1.333336 1.333328
R
2
x
13.
14.
n
MRAM
10 526.21677
20 524.25327
40 523.76240
80 523.63968
160 523.60900
n error % error
10 2.61799 0.5
20 0.65450 0.125
40 0.16362 3.12 10 2
80 0.04091 7.8 10 3
160 0.01023 2 10 3