5128_Ch03_pp098-184
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
174 Chapter 3 Derivatives<br />
EXPLORATION 1<br />
Leaving Milk on the Counter<br />
A glass of cold milk from the refrigerator is left on the counter on a warm summer<br />
day. Its temperature y (in degrees Fahrenheit) after sitting on the counter t minutes is<br />
y 72 300.98 t .<br />
Answer the following questions by interpreting y and dydt.<br />
1. What is the temperature of the refrigerator? How can you tell?<br />
2. What is the temperature of the room? How can you tell?<br />
3. When is the milk warming up the fastest? How can you tell?<br />
4. Determine algebraically when the temperature of the milk reaches 55°F.<br />
5. At what rate is the milk warming when its temperature is 55°F? Answer with<br />
an appropriate unit of measure.<br />
This equation answers what was once a<br />
perplexing problem: Is there a function<br />
with derivative x 1 ? All of the other<br />
power functions follow the Power Rule,<br />
d<br />
x n nx n1 .<br />
d x<br />
However, this formula is not much help<br />
if one is looking for a function with x 1<br />
as its derivative! Now we know why: The<br />
function we should be looking for is not<br />
a power function at all; it is the natural<br />
logarithm function.<br />
Derivative of ln x<br />
Now that we know the derivative of e x , it is relatively easy to find the derivative of its inverse<br />
function, ln x.<br />
y ln x<br />
e y x Inverse function relationship<br />
d<br />
e d x<br />
y d<br />
x<br />
d x<br />
e y dy<br />
1 d x<br />
dy 1<br />
d x e y 1 x <br />
If u is a differentiable function of x and u 0,<br />
Differentiate implicitly.<br />
d<br />
ln u 1 d x u d u<br />
.<br />
dx<br />
2<br />
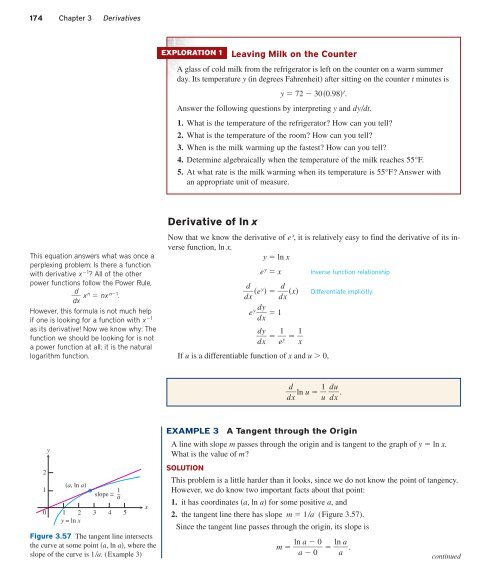
1<br />
0<br />
y<br />
(a, ln a)<br />
slope = 1 a<br />
–<br />
1 2 3 4 5<br />
y = ln x<br />
Figure 3.57 The tangent line intersects<br />
the curve at some point a, lna, where the<br />
slope of the curve is 1a. (Example 3)<br />
x<br />
EXAMPLE 3 A Tangent through the Origin<br />
A line with slope m passes through the origin and is tangent to the graph of y ln x.<br />
What is the value of m?<br />
SOLUTION<br />
This problem is a little harder than it looks, since we do not know the point of tangency.<br />
However, we do know two important facts about that point:<br />
1. it has coordinates a, lna for some positive a, and<br />
2. the tangent line there has slope m 1a (Figure 3.57).<br />
Since the tangent line passes through the origin, its slope is<br />
m ln a <br />
a <br />
0<br />
0<br />
ln a<br />
a .<br />
continued