5128_Ch03_pp098-184

170 Chapter 3 Derivatives
Quick Review 3.8 (For help, go to Sections 1.2, 1.5, and 1.6.)
In Exercises 1–5, give the domain and range of the function, and
evaluate the function at x 1.
1. y sin 1 x Domain: [1, 1]; Range: [2, 2] At 1: 2
2. y cos 1 x Domain: [1, 1]; Range: [0, ] At 1: 0
3. y tan 1 x Domain: all reals; Range: (2, 2) At 1: 4
4. y sec 1 x Domain: (∞, 1] [1, ∞); Range: [0, 2) (2, ] At 1: 0
5. y tan tan 1 x Domain: all reals; Range: all reals At 1: 1
In Exercises 6–10, find the inverse of the given function.
6. y 3x 8 f 1 (x) x 8
3
7. y 3 x 5 f 1 (x) x 3 5
8. y 8 x f 1 (x) 8 x
9. y 3x 2
x
f 1 2
(x)
3 x
10. y arctan x3 f 1 (x) 3 tan x, 2 x 2
Section 3.8 Exercises
29. (a) f(x) 3 sin x and f(x) 0. So f has a differentiable inverse by Theorem 3.
In Exercises 1–8, find the derivative of y with respect to the appropriate
27. (a) Find an equation for the line tangent to the graph of
variable.
y tan x at the point p4, 1. y 2x 2x
1
2 1
1. y cos 1 x 2 1 x
4
2. y cos 1
1x ⏐x⏐x
2 1 (b) Find an equation for the line tangent to the graph of
2
3. y sin 1 2t 4. y sin 1 1
y tan
1 t
x at the point 1, p4. y 1 2 x 1 2 4
12 2t
2t t
2
28. Let f x x 5 2x 3 x 1.
5. y sin 1 3 6
t 2 6. y s1 s 2 cos 1 s 2s2 (a) Find f 1 and f 1. f (1) 3, f(1) 12
tt
4 9
1s 2
2
7. y x sin 1 x 1 x 2 1
(b) Find f 1 3 and f 1 3. f 1 (3) 1, (f 1 1
)(3)
8. y sin
1
(sin
2x
2x) 2 1 4x
1 2
sin 1 x
29. Let f x cos x 3x.
In Exercises 9–12, a particle moves along the x-axis so that its position
(a) Show that f has a differentiable inverse.
at any time t 0 is given by x(t). Find the velocity at the indi-
(b) Find f 0 and f 0. f(0) 1, f(0) 3
cated value of t.
77
324
(c) Find f 1 1 and f 1 1. f 1 (1) 0, (f 1 )(1) 1
9. x(t) sin 1 t
4 sin1
4t
3
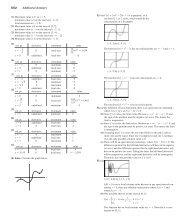
30. Group Activity Graph the function f x sin 1 sin x in
the viewing window 2p, 2p by 4, 4. Then answer the
11. x(t) tan 1 t, t 2 15 12. x(t) tan 1 (t 2 ), t 1 1
following questions:
(a) What is the domain of f ?
In Exercises 13–22, find the derivatives of y with respect to the
(b) What is the range of f ?
appropriate variable.
1
(c) At which points is f not differentiable?
13. y sec 1 2s 1 14. y sec 1 5s
⏐s⏐25s 2 1
See page 171.
(d) Sketch a graph of y f x without using NDER or
15. y csc 1 x 2 1, x 0 16. y csc 1 x2
2
computing the derivative.
17. y sec 1 1 See page 171.
⏐x⏐x
2 4
t , 0 t 1 18. y (e) Find f x algebraically. Can you reconcile your answer
cot1 t
1
See page 171.
2t(t 1)
with the graph in part (d)?
19. y cot 1 t 1 20. y s 2 1 sec 1 s
31. Group Activity A particle moves along the x-axis so that its
See page 171.
position at any time t 0 is given by x arctan t.
21. y tan 1 x 2 1 csc 1 s⏐s⏐ 1
x, x 1 0, x > 1
⏐s⏐s
2 1 (a) Prove that the particle is always moving to the right.
(b) Prove that the particle is always decelerating.
22. y cot 1 1 x tan1 x 0, x 0
In Exercises 23–26, find an equation for the tangent to the graph of y
at the indicated point.
y 0.289x 0.470
y 1 x 0.707
23. y sec 1 x, x 2 24. y tan 1 5
x, x 2
25. y sin 1 x
4 , x 3 26. y tan1 (x 2 ), x 1
y 0.378x – 0.286
y x 0.215
(c) What is the limiting position of the particle as t approaches
infinity? 2
In Exercises 32–34, use the inverse function–inverse cofunction
identities to derive the formula for the derivative of the function.
32. arccosine See page 171. 33. arccotangent See page 171.
34. arccosecant See page 171.
31. (a) v(t) d x 1
dt
1 t 2 which is always positive.
(b) a(t) d v
dt
(1
2tt 2 ) 2 which is always negative.