Dynamical Systems in Neuroscience:

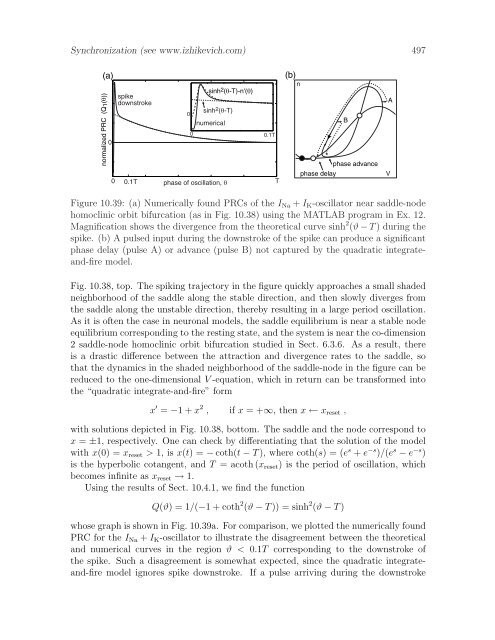
Synchronization (see www.izhikevich.com) 497(a)normalized PRC (Q1( ))0spikedownstroke00sinh 2 ( -T)-n'( )sinh 2 ( -T)numerical0.1T0 0.1T phase of oscillation,T(b)nBphase advancephase delayAVFigure 10.39: (a) Numerically found PRCs of the I Na + I K -oscillator near saddle-nodehomoclinic orbit bifurcation (as in Fig. 10.38) using the MATLAB program in Ex. 12.Magnification shows the divergence from the theoretical curve sinh 2 (ϑ − T ) during thespike. (b) A pulsed input during the downstroke of the spike can produce a significantphase delay (pulse A) or advance (pulse B) not captured by the quadratic integrateand-firemodel.Fig. 10.38, top. The spiking trajectory in the figure quickly approaches a small shadedneighborhood of the saddle along the stable direction, and then slowly diverges fromthe saddle along the unstable direction, thereby resulting in a large period oscillation.As it is often the case in neuronal models, the saddle equilibrium is near a stable nodeequilibrium corresponding to the resting state, and the system is near the co-dimension2 saddle-node homoclinic orbit bifurcation studied in Sect. 6.3.6. As a result, thereis a drastic difference between the attraction and divergence rates to the saddle, sothat the dynamics in the shaded neighborhood of the saddle-node in the figure can bereduced to the one-dimensional V -equation, which in return can be transformed intothe “quadratic integrate-and-fire” formx ′ = −1 + x 2 , if x = +∞, then x ← x reset ,with solutions depicted in Fig. 10.38, bottom. The saddle and the node correspond tox = ±1, respectively. One can check by differentiating that the solution of the modelwith x(0) = x reset > 1, is x(t) = − coth(t − T ), where coth(s) = (e s + e −s )/(e s − e −s )is the hyperbolic cotangent, and T = acoth (x reset ) is the period of oscillation, whichbecomes infinite as x reset → 1.Using the results of Sect. 10.4.1, we find the functionQ(ϑ) = 1/(−1 + coth 2 (ϑ − T )) = sinh 2 (ϑ − T )whose graph is shown in Fig. 10.39a. For comparison, we plotted the numerically foundPRC for the I Na + I K -oscillator to illustrate the disagreement between the theoreticaland numerical curves in the region ϑ < 0.1T corresponding to the downstroke ofthe spike. Such a disagreement is somewhat expected, since the quadratic integrateand-firemodel ignores spike downstroke. If a pulse arriving during the downstroke