Dynamical Systems in Neuroscience:
Dynamical Systems in Neuroscience: Dynamical Systems in Neuroscience:
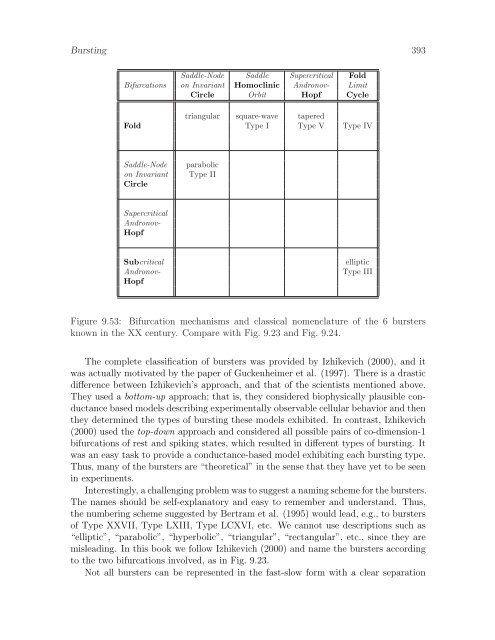
392 BurstingReview of Important Concepts• A burst of spikes is a train of action potentials followed by a periodof quiescence.• Bursting activity typically involves two time scales: fast spiking andslow modulation via a resonant current.• Many mathematical models of bursters have fast-slow formẋ = f(x, u) (fast spiking),˙u = µg(x, u) (slow modulation).• To dissect a burster, one freezes its slow subsystem (i.e., sets µ = 0)and uses the slow variable u as a bifurcation parameter to study thefast subsystem.• The fast subsystem undergoes two important bifurcations during aburst: (1) bifurcation of an equilibrium resulting in transition to spikingstate, and (2) bifurcation of a limit cycle attractor resulting intransition to resting state.• Different types of bifurcations result in different topological types ofbursting.• There are 16 basic types of bursting, summarized in Fig. 9.23.• Different topological types of bursters have different neurocomputationalproperties.Bibliographical NotesThe history of formal classification of bursting starts with the seminal paper by Rinzel(1987), who contrasted the bifurcation mechanism of the “square-wave”, “parabolic”,and “elliptic” bursters. Then, Bertram et al. (1995) followed Rinzel’s suggestionand referred to the bursters using Roman numbers, adding a new, Type IV burster.Another, “tapered” type of bursting was studied simultaneously and independently byHolden and Erneux (1993a,b), Smolen et al. (1993), and Pernarowski (1994). Laterde Vries (1998) suggested to refer to it as Type V burster. Yet another, “triangular”type of bursting was studied by Rush and Rinzel (1994), making the total number ofidentified bursters to be 6. To honor these pioneers, we described these six classicalbursters in the order consisted with the numbering nomenclature of Bertram et al.(1995). Their bifurcation mechanisms are summarized in Fig. 9.53.
Bursting 393Saddle-Node Saddle Supercritical FoldBifurcations on Invariant Homoclinic Andronov- LimitCircle Orbit Hopf Cycletriangular square-wave taperedFold Type I Type V Type IVSaddle-Nodeon InvariantCircleparabolicType IISupercriticalAndronov-HopfSubcriticalAndronov-HopfellipticType IIIFigure 9.53: Bifurcation mechanisms and classical nomenclature of the 6 burstersknown in the XX century. Compare with Fig. 9.23 and Fig. 9.24.The complete classification of bursters was provided by Izhikevich (2000), and itwas actually motivated by the paper of Guckenheimer et al. (1997). There is a drasticdifference between Izhikevich’s approach, and that of the scientists mentioned above.They used a bottom-up approach; that is, they considered biophysically plausible conductancebased models describing experimentally observable cellular behavior and thenthey determined the types of bursting these models exhibited. In contrast, Izhikevich(2000) used the top-down approach and considered all possible pairs of co-dimension-1bifurcations of rest and spiking states, which resulted in different types of bursting. Itwas an easy task to provide a conductance-based model exhibiting each bursting type.Thus, many of the bursters are “theoretical” in the sense that they have yet to be seenin experiments.Interestingly, a challenging problem was to suggest a naming scheme for the bursters.The names should be self-explanatory and easy to remember and understand. Thus,the numbering scheme suggested by Bertram et al. (1995) would lead, e.g., to burstersof Type XXVII, Type LXIII, Type LCXVI, etc. We cannot use descriptions such as“elliptic”, “parabolic”, “hyperbolic”, “triangular”, “rectangular”, etc., since they aremisleading. In this book we follow Izhikevich (2000) and name the bursters accordingto the two bifurcations involved, as in Fig. 9.23.Not all bursters can be represented in the fast-slow form with a clear separation
- Page 352 and 353: 342 Bursting(a) cortical chattering
- Page 354 and 355: 344 Burstingmembranepotential (mV)-
- Page 356 and 357: 346 Burstingvoltage-gatedCa2+-gated
- Page 358 and 359: 348 Burstingslow dynamicsneuronvolt
- Page 360 and 361: 350 Burstingslow inactivation of in
- Page 362 and 363: 352 Bursting9.2.1 Fast-slow burster
- Page 364 and 365: 354 Burstingn-nullclinen slow =-0.0
- Page 366 and 367: 356 Bursting0maxmembrane potential,
- Page 368 and 369: 358 Bursting0membrane potential, V
- Page 370 and 371: 360 BurstingI=0I=4.5425 ms 25 mVI=5
- Page 372 and 373: 362 Burstingmembrane potential, V (
- Page 374 and 375: 364 Bursting9.3 ClassificationIn Fi
- Page 376 and 377: 366 Burstingbifurcation of spiking
- Page 378 and 379: 368 BurstingFigure 9.26: Putative
- Page 380 and 381: 370 Bursting108spikingslow variable
- Page 382 and 383: 372 Bursting(a)membrane potential,
- Page 384 and 385: 374 Burstingdepending on the type o
- Page 386 and 387: 376 BurstingsubcriticalAndronov-Hop
- Page 388 and 389: 378 Bursting(a)membrane potential,
- Page 390 and 391: spiking380 Burstingfoldbifurcations
- Page 392 and 393: 382 BurstingspikingsupercriticalAnd
- Page 394 and 395: 384 Burstingaction potentials cut2
- Page 396 and 397: 386 Bursting9.4.3 BistabilitySuppos
- Page 398 and 399: 388 BurstingFigure 9.49: The instan
- Page 400 and 401: esting390 Burstingspikesynchronizat
- Page 404 and 405: 394 BurstingspikingrestingFigure 9.
- Page 406 and 407: 396 Bursting0-10membrane potential,
- Page 408 and 409: 398 Bursting0membrane potential, V
- Page 410 and 411: 400 BurstingFigure 9.61: A cycle-cy
- Page 412 and 413: 402 Bursting28. [Ph.D.] Develop an
- Page 414 and 415: 404 Synchronization (see www.izhike
- Page 416 and 417: 406 Synchronization (see www.izhike
- Page 418 and 419: 408 Solutions to Exercises, Chap. 3
- Page 420 and 421: 410 Solutions to Exercises, Chap. 3
- Page 422 and 423: 412 Solutions to Exercises, Chap. 3
- Page 424 and 425: 414 Solutions to Exercises, Chap. 4
- Page 426 and 427: 416 Solutions to Exercises, Chap. 4
- Page 428 and 429: 418 Solutions to Exercises, Chap. 4
- Page 430 and 431: 420 Solutions to Exercises, Chap. 4
- Page 432 and 433: 422 Solutions to Exercises, Chap. 5
- Page 434 and 435: 424 Solutions to Exercises, Chap. 6
- Page 436 and 437: 426 Solutions to Exercises, Chap. 6
- Page 438 and 439: 428 Solutions to Exercises, Chap. 8
- Page 440 and 441: 430 Solutions to Exercises, Chap. 9
- Page 442 and 443: 432 Solutions to Exercises, Chap. 9
- Page 444 and 445: 434 Solutions to Exercises, Chap. 9
- Page 446 and 447: 436 Solutions to Exercises, Chap. 9
- Page 448 and 449: 438 Solutions to Exercises, Chap. 9
- Page 450 and 451: 440 Solutions to Exercises, Chap. 9
Burst<strong>in</strong>g 393Saddle-Node Saddle Supercritical FoldBifurcations on Invariant Homocl<strong>in</strong>ic Andronov- LimitCircle Orbit Hopf Cycletriangular square-wave taperedFold Type I Type V Type IVSaddle-Nodeon InvariantCircleparabolicType IISupercriticalAndronov-HopfSubcriticalAndronov-HopfellipticType IIIFigure 9.53: Bifurcation mechanisms and classical nomenclature of the 6 burstersknown <strong>in</strong> the XX century. Compare with Fig. 9.23 and Fig. 9.24.The complete classification of bursters was provided by Izhikevich (2000), and itwas actually motivated by the paper of Guckenheimer et al. (1997). There is a drasticdifference between Izhikevich’s approach, and that of the scientists mentioned above.They used a bottom-up approach; that is, they considered biophysically plausible conductancebased models describ<strong>in</strong>g experimentally observable cellular behavior and thenthey determ<strong>in</strong>ed the types of burst<strong>in</strong>g these models exhibited. In contrast, Izhikevich(2000) used the top-down approach and considered all possible pairs of co-dimension-1bifurcations of rest and spik<strong>in</strong>g states, which resulted <strong>in</strong> different types of burst<strong>in</strong>g. Itwas an easy task to provide a conductance-based model exhibit<strong>in</strong>g each burst<strong>in</strong>g type.Thus, many of the bursters are “theoretical” <strong>in</strong> the sense that they have yet to be seen<strong>in</strong> experiments.Interest<strong>in</strong>gly, a challeng<strong>in</strong>g problem was to suggest a nam<strong>in</strong>g scheme for the bursters.The names should be self-explanatory and easy to remember and understand. Thus,the number<strong>in</strong>g scheme suggested by Bertram et al. (1995) would lead, e.g., to burstersof Type XXVII, Type LXIII, Type LCXVI, etc. We cannot use descriptions such as“elliptic”, “parabolic”, “hyperbolic”, “triangular”, “rectangular”, etc., s<strong>in</strong>ce they aremislead<strong>in</strong>g. In this book we follow Izhikevich (2000) and name the bursters accord<strong>in</strong>gto the two bifurcations <strong>in</strong>volved, as <strong>in</strong> Fig. 9.23.Not all bursters can be represented <strong>in</strong> the fast-slow form with a clear separation