Dynamical Systems in Neuroscience:

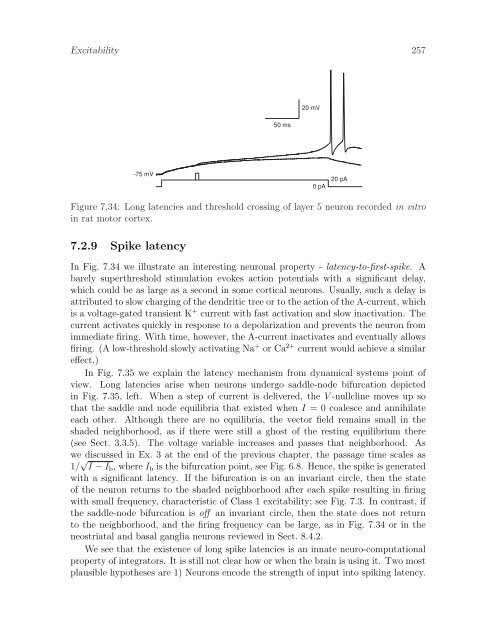
Excitability 25720 mV50 ms-75 mV0 pA20 pAFigure 7.34: Long latencies and threshold crossing of layer 5 neuron recorded in vitroin rat motor cortex.7.2.9 Spike latencyIn Fig. 7.34 we illustrate an interesting neuronal property - latency-to-first-spike. Abarely superthreshold stimulation evokes action potentials with a significant delay,which could be as large as a second in some cortical neurons. Usually, such a delay isattributed to slow charging of the dendritic tree or to the action of the A-current, whichis a voltage-gated transient K + current with fast activation and slow inactivation. Thecurrent activates quickly in response to a depolarization and prevents the neuron fromimmediate firing. With time, however, the A-current inactivates and eventually allowsfiring. (A low-threshold slowly activating Na + or Ca 2+ current would achieve a similareffect.)In Fig. 7.35 we explain the latency mechanism from dynamical systems point ofview. Long latencies arise when neurons undergo saddle-node bifurcation depictedin Fig. 7.35, left. When a step of current is delivered, the V -nullcline moves up sothat the saddle and node equilibria that existed when I = 0 coalesce and annihilateeach other. Although there are no equilibria, the vector field remains small in theshaded neighborhood, as if there were still a ghost of the resting equilibrium there(see Sect. 3.3.5). The voltage variable increases and passes that neighborhood. Aswe discussed in Ex. 3 at the end of the previous chapter, the passage time scales as1/ √ I − I b , where I b is the bifurcation point, see Fig. 6.8. Hence, the spike is generatedwith a significant latency. If the bifurcation is on an invariant circle, then the stateof the neuron returns to the shaded neighborhood after each spike resulting in firingwith small frequency, characteristic of Class 1 excitability; see Fig. 7.3. In contrast, ifthe saddle-node bifurcation is off an invariant circle, then the state does not returnto the neighborhood, and the firing frequency can be large, as in Fig. 7.34 or in theneostriatal and basal ganglia neurons reviewed in Sect. 8.4.2.We see that the existence of long spike latencies is an innate neuro-computationalproperty of integrators. It is still not clear how or when the brain is using it. Two mostplausible hypotheses are 1) Neurons encode the strength of input into spiking latency.